
Previous in Relation and Functions Next in Relation and Functions
Question Number 101342 by mathmax by abdo last updated on 02/Jul/20
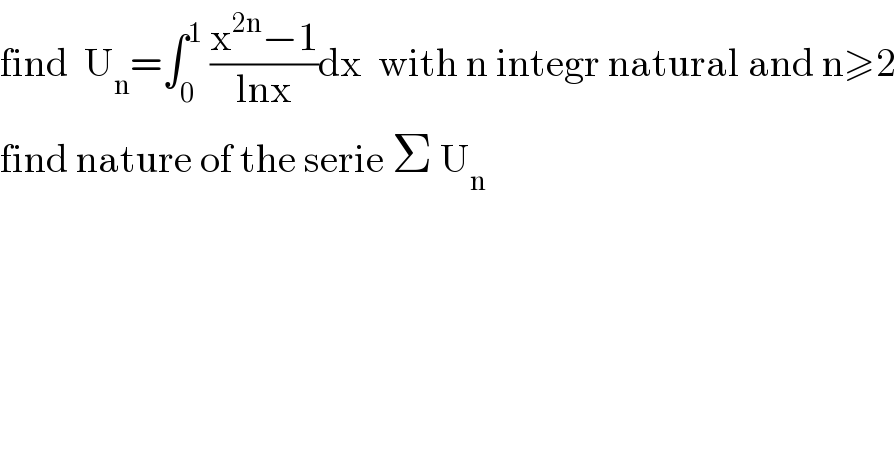
$$\mathrm{find}\:\:\mathrm{U}_{\mathrm{n}} =\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\mathrm{x}^{\mathrm{2n}} −\mathrm{1}}{\mathrm{lnx}}\mathrm{dx}\:\:\mathrm{with}\:\mathrm{n}\:\mathrm{integr}\:\mathrm{natural}\:\mathrm{and}\:\mathrm{n}\geqslant\mathrm{2} \\ $$$$\mathrm{find}\:\mathrm{nature}\:\mathrm{of}\:\mathrm{the}\:\mathrm{serie}\:\Sigma\:\mathrm{U}_{\mathrm{n}} \\ $$
Answered by mathmax by abdo last updated on 04/Jul/20
![U_n =∫_0 ^1 ((x^(2n) −1)/(lnx))dx changement lnx =−t give x =e^(−t) U_n =−∫_0 ^∞ ((e^(−2nt) −1)/(−t))(−e^(−t) )dt =−∫_0 ^∞ ((e^(−(2n+1)t) −e^(−t) )/t)dt =∫_0 ^∞ ((e^(−t) −e^(−(2n+1)t) )/t)dt let f(x) =∫_0 ^∞ ((e^(−t) −e^(−(2n+1)t) )/t)e^(−xt) dt withx>0 ⇒ f^′ (x) =−∫_0 ^∞ (e^(−(1+x)t) −e^(−(2n+1+x)t) )dt =∫_0 ^∞ (e^(−(2n+1+x)t) −e^(−(1+x)t) )dt =[((−1)/((2n+1+x)))e^(−(2n+1+x)t) +(1/(1+x))e^(−(1+x)t) ]_0 ^(+∞) =(1/(2n+1+x))−(1/(1+x)) ⇒f(x) =∫ (dx/(x+2n+1))−∫ (dx/(x+1)) +c =ln(((x+2n+1)/(x+1))) +c we have c =lim_(x→+∞) f(x) =0 ⇒ f(x) =ln(((x+2n+1)/(x+1))) and U_n =f(0) =ln(2n+1) lim_(n→+∞) U_n =+∞ ⇒ Σ U_n is divergent](Q101738.png)
$$\mathrm{U}_{\mathrm{n}} =\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\mathrm{x}^{\mathrm{2n}} −\mathrm{1}}{\mathrm{lnx}}\mathrm{dx}\:\mathrm{changement}\:\mathrm{lnx}\:=−\mathrm{t}\:\mathrm{give}\:\mathrm{x}\:=\mathrm{e}^{−\mathrm{t}} \\ $$$$\mathrm{U}_{\mathrm{n}} =−\int_{\mathrm{0}} ^{\infty} \:\:\frac{\mathrm{e}^{−\mathrm{2nt}} −\mathrm{1}}{−\mathrm{t}}\left(−\mathrm{e}^{−\mathrm{t}} \right)\mathrm{dt}\:=−\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{e}^{−\left(\mathrm{2n}+\mathrm{1}\right)\mathrm{t}} −\mathrm{e}^{−\mathrm{t}} }{\mathrm{t}}\mathrm{dt} \\ $$$$=\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{e}^{−\mathrm{t}} −\mathrm{e}^{−\left(\mathrm{2n}+\mathrm{1}\right)\mathrm{t}} }{\mathrm{t}}\mathrm{dt}\:\:\mathrm{let}\:\mathrm{f}\left(\mathrm{x}\right)\:=\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{e}^{−\mathrm{t}} −\mathrm{e}^{−\left(\mathrm{2n}+\mathrm{1}\right)\mathrm{t}} }{\mathrm{t}}\mathrm{e}^{−\mathrm{xt}} \:\mathrm{dt}\:\:\mathrm{withx}>\mathrm{0}\:\Rightarrow \\ $$$$\mathrm{f}^{'} \left(\mathrm{x}\right)\:=−\int_{\mathrm{0}} ^{\infty} \:\:\left(\mathrm{e}^{−\left(\mathrm{1}+\mathrm{x}\right)\mathrm{t}} −\mathrm{e}^{−\left(\mathrm{2n}+\mathrm{1}+\mathrm{x}\right)\mathrm{t}} \right)\mathrm{dt} \\ $$$$=\int_{\mathrm{0}} ^{\infty} \left(\mathrm{e}^{−\left(\mathrm{2n}+\mathrm{1}+\mathrm{x}\right)\mathrm{t}} −\mathrm{e}^{−\left(\mathrm{1}+\mathrm{x}\right)\mathrm{t}} \right)\mathrm{dt}\:=\left[\frac{−\mathrm{1}}{\left(\mathrm{2n}+\mathrm{1}+\mathrm{x}\right)}\mathrm{e}^{−\left(\mathrm{2n}+\mathrm{1}+\mathrm{x}\right)\mathrm{t}} +\frac{\mathrm{1}}{\mathrm{1}+\mathrm{x}}\mathrm{e}^{−\left(\mathrm{1}+\mathrm{x}\right)\mathrm{t}} \right]_{\mathrm{0}} ^{+\infty} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2n}+\mathrm{1}+\mathrm{x}}−\frac{\mathrm{1}}{\mathrm{1}+\mathrm{x}}\:\Rightarrow\mathrm{f}\left(\mathrm{x}\right)\:=\int\:\frac{\mathrm{dx}}{\mathrm{x}+\mathrm{2n}+\mathrm{1}}−\int\:\frac{\mathrm{dx}}{\mathrm{x}+\mathrm{1}}\:+\mathrm{c} \\ $$$$=\mathrm{ln}\left(\frac{\mathrm{x}+\mathrm{2n}+\mathrm{1}}{\mathrm{x}+\mathrm{1}}\right)\:+\mathrm{c}\:\:\:\mathrm{we}\:\mathrm{have}\:\mathrm{c}\:=\mathrm{lim}_{\mathrm{x}\rightarrow+\infty} \mathrm{f}\left(\mathrm{x}\right)\:=\mathrm{0}\:\Rightarrow \\ $$$$\mathrm{f}\left(\mathrm{x}\right)\:=\mathrm{ln}\left(\frac{\mathrm{x}+\mathrm{2n}+\mathrm{1}}{\mathrm{x}+\mathrm{1}}\right)\:\:\mathrm{and}\:\mathrm{U}_{\mathrm{n}} =\mathrm{f}\left(\mathrm{0}\right)\:=\mathrm{ln}\left(\mathrm{2n}+\mathrm{1}\right) \\ $$$$\mathrm{lim}_{\mathrm{n}\rightarrow+\infty} \:\mathrm{U}_{\mathrm{n}} =+\infty\:\Rightarrow\:\Sigma\:\mathrm{U}_{\mathrm{n}} \:\mathrm{is}\:\mathrm{divergent} \\ $$
