Question Number 101345 by bobhans last updated on 02/Jul/20

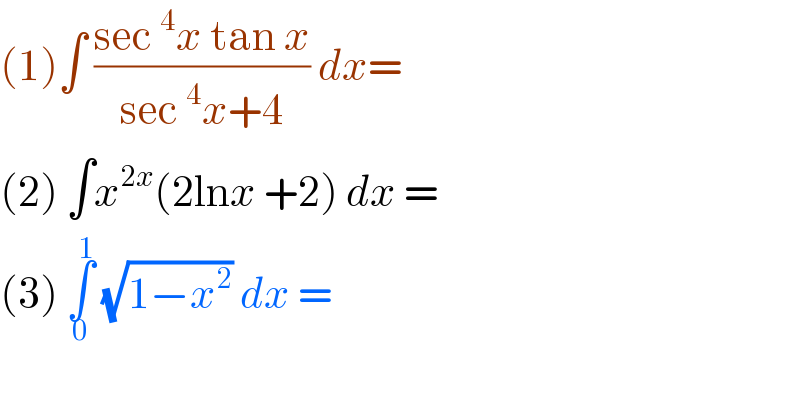
(1)∫ ((sec ^4 x tan x)/(sec ^4 x+4)) dx= (2) ∫x^(2x) (2lnx +2) dx = (3) ∫_0 ^1 (√(1−x^2 )) dx =

Commented byjohn santu last updated on 02/Jul/20

(1)∫ ((sec ^4 x tan x)/(sec ^4 x +4)) dx set : z = sec ^4 x + 4 → sec ^4 x tan x dx =(1/4) dz I = (1/4)∫ (dz/z) = (1/4) ln ∣z∣ + c = (1/4) ln ∣sec ^4 x + 4∣ + c (2) ∫ x^(2x) (2 ln x +2) dx apply a^b = e^(b ln a) J = ∫ e^(2x ln (x) ) (2ln x +2) dx let q = 2x ln x → dq = (2ln x +2)dx J= ∫ e^q dq = e^q + c = x^(2x) + c (3) ∫_0 ^1 (√(1−x^2 )) dx = (π/4) long way : set: sin s = x G = ∫_0 ^(π/2) (√(1−sin ^2 s)) cos s ds G= ∫_0 ^(π/2) [ (1/2) + (1/2) cos (2s)] ds = [(1/2)s + (1/4) sin (2s) ]_0 ^(π/2) = (π/4) ♠♥⧫

Commented bybramlex last updated on 02/Jul/20

♥⧫♠

Commented bybobhans last updated on 02/Jul/20

thank you