Question and Answers Forum

All Questions      Topic List

Limits Questions

Previous in All Question      Next in All Question      

Previous in Limits      Next in Limits      

Question Number 101422 by john santu last updated on 02/Jul/20

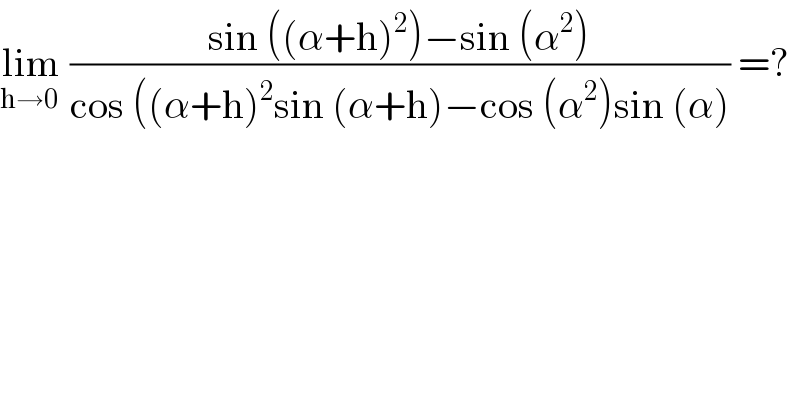
lim_(h→0 ) ((sin ((α+h)^2 )−sin (α^2 ))/(cos ((α+h)^2 sin (α+h)−cos (α^2 )sin (α))) =?

$$\underset{\mathrm{h}\rightarrow\mathrm{0}\:} {\mathrm{lim}}\:\frac{\mathrm{sin}\:\left(\left(\alpha+\mathrm{h}\right)^{\mathrm{2}} \right)−\mathrm{sin}\:\left(\alpha^{\mathrm{2}} \right)}{\mathrm{cos}\:\left(\left(\alpha+\mathrm{h}\right)^{\mathrm{2}} \mathrm{sin}\:\left(\alpha+\mathrm{h}\right)−\mathrm{cos}\:\left(\alpha^{\mathrm{2}} \right)\mathrm{sin}\:\left(\alpha\right)\right.}\:=? \\ $$

Commented by john santu last updated on 02/Jul/20

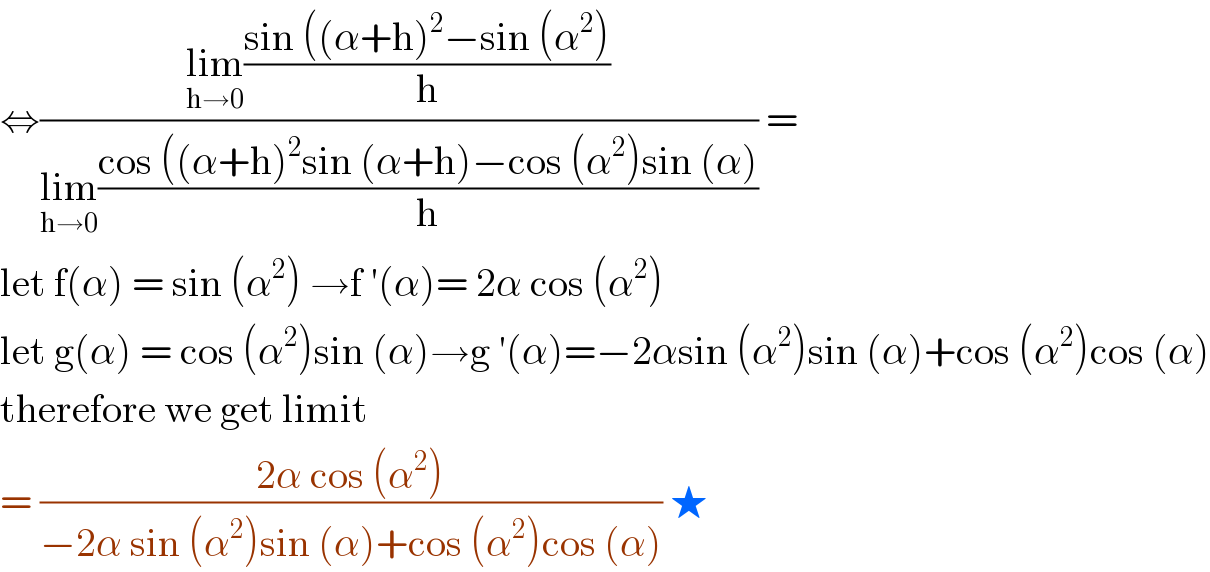
⇔((lim_(h→0) ((sin ((α+h)^2 −sin (α^2 ))/h))/(lim_(h→0) ((cos ((α+h)^2 sin (α+h)−cos (α^2 )sin (α))/h))) = let f(α) = sin (α^2 ) →f ′(α)= 2α cos (α^2 ) let g(α) = cos (α^2 )sin (α)→g ′(α)=−2αsin (α^2 )sin (α)+cos (α^2 )cos (α) therefore we get limit = ((2α cos (α^2 ))/(−2α sin (α^2 )sin (α)+cos (α^2 )cos (α))) ★

$$\Leftrightarrow\frac{\underset{\mathrm{h}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{sin}\:\left(\left(\alpha+\mathrm{h}\right)^{\mathrm{2}} −\mathrm{sin}\:\left(\alpha^{\mathrm{2}} \right)\right.}{\mathrm{h}}}{\underset{\mathrm{h}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{cos}\:\left(\left(\alpha+\mathrm{h}\right)^{\mathrm{2}} \mathrm{sin}\:\left(\alpha+\mathrm{h}\right)−\mathrm{cos}\:\left(\alpha^{\mathrm{2}} \right)\mathrm{sin}\:\left(\alpha\right)\right.}{\mathrm{h}}}\:= \\ $$$$\mathrm{let}\:\mathrm{f}\left(\alpha\right)\:=\:\mathrm{sin}\:\left(\alpha^{\mathrm{2}} \right)\:\rightarrow\mathrm{f}\:'\left(\alpha\right)=\:\mathrm{2}\alpha\:\mathrm{cos}\:\left(\alpha^{\mathrm{2}} \right) \\ $$$$\mathrm{let}\:\mathrm{g}\left(\alpha\right)\:=\:\mathrm{cos}\:\left(\alpha^{\mathrm{2}} \right)\mathrm{sin}\:\left(\alpha\right)\rightarrow\mathrm{g}\:'\left(\alpha\right)=−\mathrm{2}\alpha\mathrm{sin}\:\left(\alpha^{\mathrm{2}} \right)\mathrm{sin}\:\left(\alpha\right)+\mathrm{cos}\:\left(\alpha^{\mathrm{2}} \right)\mathrm{cos}\:\left(\alpha\right) \\ $$$$\mathrm{therefore}\:\mathrm{we}\:\mathrm{get}\:\mathrm{limit} \\ $$$$=\:\frac{\mathrm{2}\alpha\:\mathrm{cos}\:\left(\alpha^{\mathrm{2}} \right)}{−\mathrm{2}\alpha\:\mathrm{sin}\:\left(\alpha^{\mathrm{2}} \right)\mathrm{sin}\:\left(\alpha\right)+\mathrm{cos}\:\left(\alpha^{\mathrm{2}} \right)\mathrm{cos}\:\left(\alpha\right)}\:\bigstar \\ $$

Commented by Dwaipayan Shikari last updated on 02/Jul/20

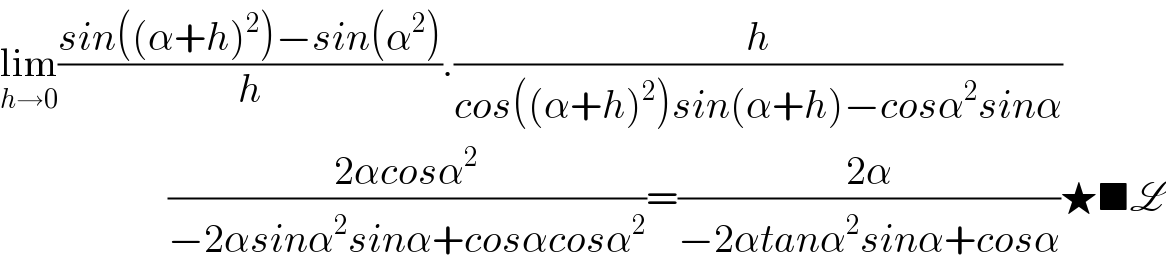
lim_(h→0) ((sin((α+h)^2 )−sin(α^2 ))/h).(h/(cos((α+h)^2 )sin(α+h)−cosα^2 sinα)) ((2αcosα^2 )/(−2αsinα^2 sinα+cosαcosα^2 ))=((2α)/(−2αtanα^2 sinα+cosα))★■L

$$\underset{{h}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{{sin}\left(\left(\alpha+{h}\right)^{\mathrm{2}} \right)−{sin}\left(\alpha^{\mathrm{2}} \right)}{{h}}.\frac{{h}}{{cos}\left(\left(\alpha+{h}\right)^{\mathrm{2}} \right){sin}\left(\alpha+{h}\right)−{cos}\alpha^{\mathrm{2}} {sin}\alpha} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\frac{\mathrm{2}\alpha{cos}\alpha^{\mathrm{2}} }{−\mathrm{2}\alpha{sin}\alpha^{\mathrm{2}} {sin}\alpha+{cos}\alpha{cos}\alpha^{\mathrm{2}} }=\frac{\mathrm{2}\alpha}{−\mathrm{2}\alpha{tan}\alpha^{\mathrm{2}} {sin}\alpha+{cos}\alpha}\bigstar\blacksquare\mathscr{L} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com