
Question Number 101461 by Dwaipayan Shikari last updated on 02/Jul/20
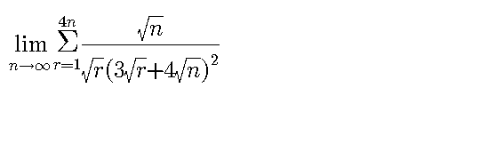
Answered by MAB last updated on 02/Jul/20
![lim_(n→∞) Σ_(r=1) ^(4n) ((√n)/((√r)(3(√r)+4(√n))^2 ))=lim_(n→∞) (1/n)Σ_(r=1) ^(4n) (1/((√(r/n))(3(√(r/n))+4)^2 )) =lim_(N→∞) (1/N)Σ_(r=1) ^N (2/((√(r/N))(6(√(r/N))+4)^2 )) (4n=N) =∫_0 ^1 (2/((√x)(6(√x)+4)^2 ))dx (u=(√x)) =∫_0 ^1 (2/(u(6u+4)^2 ))2udu =∫_0 ^1 (1/((3u+2)^2 ))du =[((−1)/3)∙(1/(3u+2))]_0 ^1 =(1/(10)) finally: lim_(n→∞) Σ_(r=1) ^(4n) ((√n)/((√r)(3(√r)+4(√n))^2 ))=(1/(10))](Q101463.png)
$$\underset{{n}\rightarrow\infty} {\mathrm{lim}}\underset{{r}=\mathrm{1}} {\overset{\mathrm{4}{n}} {\sum}}\frac{\sqrt{{n}}}{\sqrt{{r}}\left(\mathrm{3}\sqrt{{r}}+\mathrm{4}\sqrt{{n}}\right)^{\mathrm{2}} }=\underset{{n}\rightarrow\infty} {\mathrm{lim}}\frac{\mathrm{1}}{{n}}\underset{{r}=\mathrm{1}} {\overset{\mathrm{4}{n}} {\sum}}\frac{\mathrm{1}}{\sqrt{\frac{{r}}{{n}}}\left(\mathrm{3}\sqrt{\frac{{r}}{{n}}}+\mathrm{4}\right)^{\mathrm{2}} } \\ $$$$=\underset{{N}\rightarrow\infty} {\mathrm{lim}}\frac{\mathrm{1}}{{N}}\underset{{r}=\mathrm{1}} {\overset{{N}} {\sum}}\frac{\mathrm{2}}{\sqrt{\frac{{r}}{{N}}}\left(\mathrm{6}\sqrt{\frac{{r}}{{N}}}+\mathrm{4}\right)^{\mathrm{2}} }\:\:\left(\mathrm{4}{n}={N}\right) \\ $$$$=\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{2}}{\sqrt{{x}}\left(\mathrm{6}\sqrt{{x}}+\mathrm{4}\right)^{\mathrm{2}} }{dx}\:\:\:\left({u}=\sqrt{{x}}\right) \\ $$$$=\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{2}}{{u}\left(\mathrm{6}{u}+\mathrm{4}\right)^{\mathrm{2}} }\mathrm{2}{udu} \\ $$$$=\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{1}}{\left(\mathrm{3}{u}+\mathrm{2}\right)^{\mathrm{2}} }{du} \\ $$$$=\left[\frac{−\mathrm{1}}{\mathrm{3}}\centerdot\frac{\mathrm{1}}{\mathrm{3}{u}+\mathrm{2}}\right]_{\mathrm{0}} ^{\mathrm{1}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{10}} \\ $$$${finally}: \\ $$$$\underset{{n}\rightarrow\infty} {\mathrm{lim}}\underset{{r}=\mathrm{1}} {\overset{\mathrm{4}{n}} {\sum}}\frac{\sqrt{{n}}}{\sqrt{{r}}\left(\mathrm{3}\sqrt{{r}}+\mathrm{4}\sqrt{{n}}\right)^{\mathrm{2}} }=\frac{\mathrm{1}}{\mathrm{10}} \\ $$$$ \\ $$
Commented by Dwaipayan Shikari last updated on 02/Jul/20
Thanking you
Commented by MAB last updated on 02/Jul/20

$${you}\:{are}\:{welcome} \\ $$
