Question and Answers Forum

All Questions      Topic List

Integration Questions

Previous in All Question      Next in All Question      

Previous in Integration      Next in Integration      

Question Number 101493 by bemath last updated on 03/Jul/20

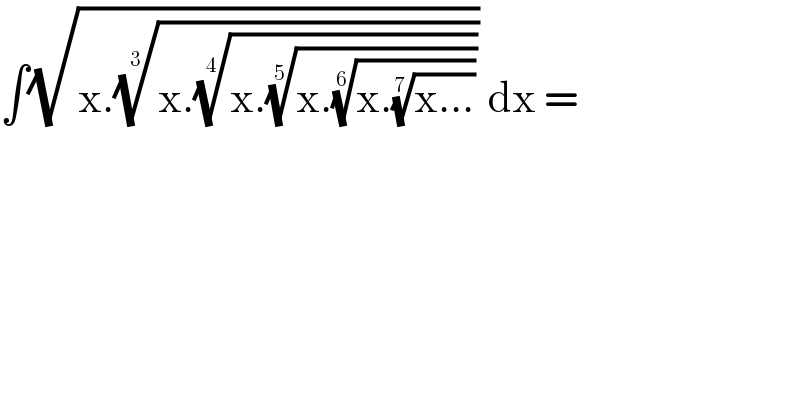
∫(√(x.((x.((x.((x.((x.((x...))^(1/7) ))^(1/6) ))^(1/5) ))^(1/4) ))^(1/3) )) dx =

$$\int\sqrt{\mathrm{x}.\sqrt[{\mathrm{3}}]{\mathrm{x}.\sqrt[{\mathrm{4}}]{\mathrm{x}.\sqrt[{\mathrm{5}}]{\mathrm{x}.\sqrt[{\mathrm{6}}]{\mathrm{x}.\sqrt[{\mathrm{7}}]{\mathrm{x}...}}}}}}\:\mathrm{dx}\:=\: \\ $$$$ \\ $$

Answered by floor(10²Eta[1]) last updated on 03/Jul/20

let′s see a small case first to understand better whats going on (√(x.((x(x)^(1/4) ))^(1/3) ))=(x(x(x)^(1/4) )^(1/3) )^(1/2) =x^(1/2) .x^((1/2)×(1/3)) .x^((1/2)×(1/3)×(1/4)) =x^((1/2)+(1/(2.3))+(1/(2.3.4))) =x^((1/(2!))+(1/(3!))+(1/(4!))) so back to the initial problem, we have: =∫x^((1/(2!))+(1/(3!))+(1/(4!))+...) dx now we want to get a close form for this expression on the exponent: (1/(2!))+(1/(3!))+(1/(4!))+...=Σ_(n=2) ^∞ (1/(n!)) from the taylor series expansion to e^x we have that e^x =Σ_(n=0) ^∞ (x^n /(n!)) when x=1: e=Σ_(n=0) ^∞ (1/(n!))=(1/(0!))+(1/(1!))+Σ_(n=2) ^∞ (1/(n!))=2+Σ_(n=2) ^∞ (1/(n!)) ⇒Σ_(n=2) ^∞ (1/(n!))=e−2 ⇒∫x^((1/(2!))+(1/(3!))+...) dx=∫x^(e−2) dx=(x^(e−1) /(e−1))+C

$${let}'{s}\:{see}\:{a}\:{small}\:{case}\:{first}\:{to}\:{understand} \\ $$$${better}\:{whats}\:{going}\:{on} \\ $$$$\sqrt{{x}.\sqrt[{\mathrm{3}}]{{x}\sqrt[{\mathrm{4}}]{{x}}}}=\left({x}\left({x}\left({x}\right)^{\mathrm{1}/\mathrm{4}} \right)^{\mathrm{1}/\mathrm{3}} \right)^{\mathrm{1}/\mathrm{2}} ={x}^{\frac{\mathrm{1}}{\mathrm{2}}} .{x}^{\frac{\mathrm{1}}{\mathrm{2}}×\frac{\mathrm{1}}{\mathrm{3}}} .{x}^{\frac{\mathrm{1}}{\mathrm{2}}×\frac{\mathrm{1}}{\mathrm{3}}×\frac{\mathrm{1}}{\mathrm{4}}} \\ $$$$={x}^{\frac{\mathrm{1}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{2}.\mathrm{3}}+\frac{\mathrm{1}}{\mathrm{2}.\mathrm{3}.\mathrm{4}}} ={x}^{\frac{\mathrm{1}}{\mathrm{2}!}+\frac{\mathrm{1}}{\mathrm{3}!}+\frac{\mathrm{1}}{\mathrm{4}!}} \\ $$$${so}\:{back}\:{to}\:{the}\:{initial}\:{problem},\:{we}\:{have}: \\ $$$$=\int{x}^{\frac{\mathrm{1}}{\mathrm{2}!}+\frac{\mathrm{1}}{\mathrm{3}!}+\frac{\mathrm{1}}{\mathrm{4}!}+...} {dx} \\ $$$${now}\:{we}\:{want}\:{to}\:{get}\:{a}\:{close}\:{form}\:{for}\:{this}\:{expression}\:{on}\:{the}\:{exponent}: \\ $$$$\frac{\mathrm{1}}{\mathrm{2}!}+\frac{\mathrm{1}}{\mathrm{3}!}+\frac{\mathrm{1}}{\mathrm{4}!}+...=\underset{{n}=\mathrm{2}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{{n}!} \\ $$$${from}\:{the}\:{taylor}\:{series}\:{expansion}\:{to}\:{e}^{{x}} \:{we}\:{have}\:{that} \\ $$$${e}^{{x}} =\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{{x}^{{n}} }{{n}!} \\ $$$${when}\:{x}=\mathrm{1}: \\ $$$${e}=\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{{n}!}=\frac{\mathrm{1}}{\mathrm{0}!}+\frac{\mathrm{1}}{\mathrm{1}!}+\underset{{n}=\mathrm{2}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{{n}!}=\mathrm{2}+\underset{{n}=\mathrm{2}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{{n}!} \\ $$$$\Rightarrow\underset{{n}=\mathrm{2}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{{n}!}={e}−\mathrm{2} \\ $$$$\Rightarrow\int{x}^{\frac{\mathrm{1}}{\mathrm{2}!}+\frac{\mathrm{1}}{\mathrm{3}!}+...} {dx}=\int{x}^{{e}−\mathrm{2}} {dx}=\frac{{x}^{{e}−\mathrm{1}} }{{e}−\mathrm{1}}+{C} \\ $$

Commented by 1549442205 last updated on 03/Jul/20

A great work !

$$\mathrm{A}\:\mathrm{great}\:\mathrm{work}\:! \\ $$

Commented by bemath last updated on 03/Jul/20

coll ������

Terms of Service

Privacy Policy

Contact: info@tinkutara.com