Question and Answers Forum

All Questions      Topic List

Integration Questions

Previous in All Question      Next in All Question      

Previous in Integration      Next in Integration      

Question Number 101531 by mhmd last updated on 03/Jul/20

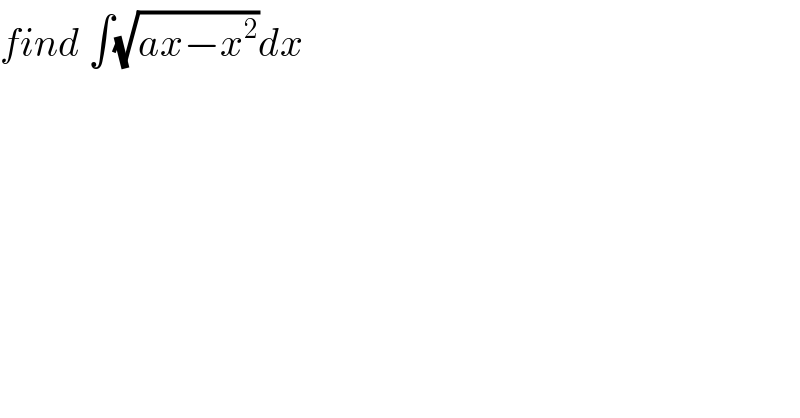
find ∫(√(ax−x^2 ))dx

$${find}\:\int\sqrt{{ax}−{x}^{\mathrm{2}} }{dx} \\ $$

Answered by Mr.D.N. last updated on 03/Jul/20

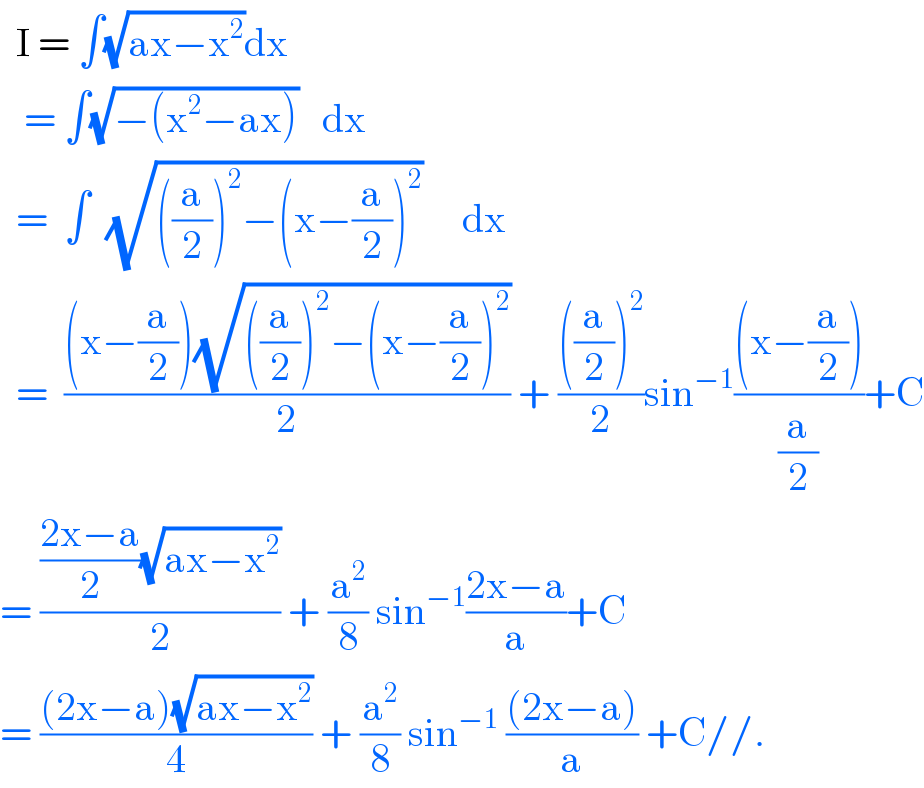
I = ∫(√(ax−x^2 ))dx = ∫(√(−(x^2 −ax))) dx = ∫ (√(((a/2))^2 −(x−(a/2))^2 )) dx = (((x−(a/2))(√(((a/2))^2 −(x−(a/2))^2 )))/2) + ((((a/2))^2 )/2)sin^(−1) (((x−(a/2)))/(a/2))+C = ((((2x−a)/2)(√(ax−x^2 )))/2) + (a^2 /8) sin^(−1) ((2x−a)/a)+C = (((2x−a)(√(ax−x^2 )))/4) + (a^2 /8) sin^(−1) (((2x−a))/a) +C//.

$$\:\:\mathrm{I}\:=\:\int\sqrt{\mathrm{ax}−\mathrm{x}^{\mathrm{2}} }\mathrm{dx} \\ $$$$\:\:\:=\:\int\sqrt{−\left(\mathrm{x}^{\mathrm{2}} −\mathrm{ax}\right)}\:\:\:\mathrm{dx} \\ $$$$\:\:=\:\:\int\:\:\sqrt{\left(\frac{\mathrm{a}}{\mathrm{2}}\right)^{\mathrm{2}} −\left(\mathrm{x}−\frac{\mathrm{a}}{\mathrm{2}}\right)^{\mathrm{2}} }\:\:\:\:\:\mathrm{dx} \\ $$$$\:\:=\:\:\frac{\left(\mathrm{x}−\frac{\mathrm{a}}{\mathrm{2}}\right)\sqrt{\left(\frac{\mathrm{a}}{\mathrm{2}}\right)^{\mathrm{2}} −\left(\mathrm{x}−\frac{\mathrm{a}}{\mathrm{2}}\right)^{\mathrm{2}} }}{\mathrm{2}}\:+\:\frac{\left(\frac{\mathrm{a}}{\mathrm{2}}\right)^{\mathrm{2}} }{\mathrm{2}}\mathrm{sin}^{−\mathrm{1}} \frac{\left(\mathrm{x}−\frac{\mathrm{a}}{\mathrm{2}}\right)}{\frac{\mathrm{a}}{\mathrm{2}}}+\mathrm{C} \\ $$$$=\:\frac{\frac{\mathrm{2x}−\mathrm{a}}{\mathrm{2}}\sqrt{\mathrm{ax}−\mathrm{x}^{\mathrm{2}} }}{\mathrm{2}}\:+\:\frac{\mathrm{a}^{\mathrm{2}} }{\mathrm{8}}\:\mathrm{sin}^{−\mathrm{1}} \frac{\mathrm{2x}−\mathrm{a}}{\mathrm{a}}+\mathrm{C} \\ $$$$=\:\frac{\left(\mathrm{2x}−\mathrm{a}\right)\sqrt{\mathrm{ax}−\mathrm{x}^{\mathrm{2}} }}{\mathrm{4}}\:+\:\frac{\mathrm{a}^{\mathrm{2}} }{\mathrm{8}}\:\mathrm{sin}^{−\mathrm{1}} \:\frac{\left(\mathrm{2x}−\mathrm{a}\right)}{\mathrm{a}}\:+\mathrm{C}//. \\ $$

Commented by mhmd last updated on 03/Jul/20

thank you sir

$${thank}\:{you}\:{sir} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com