Question Number 101551 by mhmd last updated on 03/Jul/20

Answered by bobhans last updated on 03/Jul/20

(Q2) The area = ∫_0 ^1 ∫_0 ^x dy dx = ∫_0 ^1 (y)]_0 ^x dx = ∫_0 ^1 x dx = [ (1/2)x^2 ]_0 ^1 = (1/2) ♥

Commented bymhmd last updated on 03/Jul/20

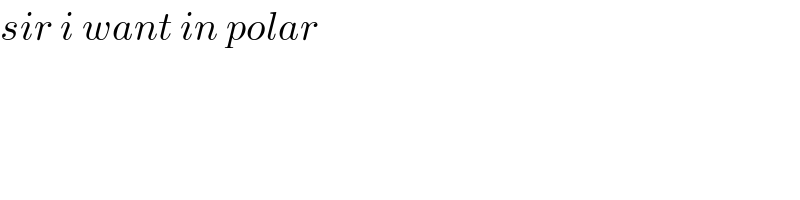
sir i want in polar

Answered by mr W last updated on 04/Jul/20

Q2(b) 1−r cos θ=r sin θ ⇒r=(1/(sin θ+cos θ)) A=∫_0 ^(π/2) ∫_0 ^(1/(sin θ+cos θ)) ρdρdθ =(1/2)∫_0 ^(π/2) (1/((sin θ+cos θ)^2 ))dθ =(1/2)∫_0 ^(π/2) (1/(1+sin 2θ))dθ =(1/4)∫_0 ^(π/2) (1/(1+sin 2θ))d(2θ) =(1/4)∫_0 ^π (1/(1+sin t))dt =(1/4)[(2/(1+tan (t/2)))]_π ^0 =(1/2)(1−0) =(1/2)