Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 101563 by harckinwunmy last updated on 03/Jul/20

Answered by bramlex last updated on 03/Jul/20

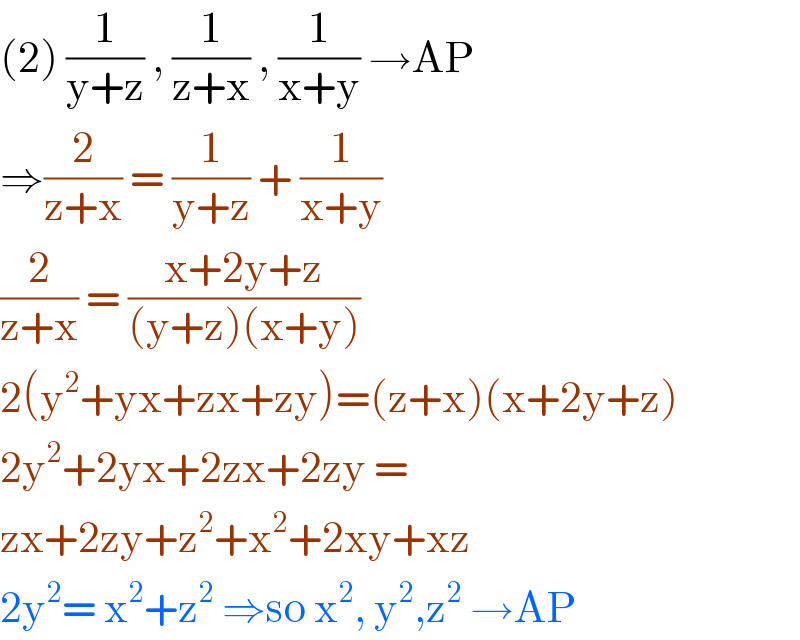
(2) (1/(y+z)) , (1/(z+x)) , (1/(x+y)) →AP ⇒(2/(z+x)) = (1/(y+z)) + (1/(x+y)) (2/(z+x)) = ((x+2y+z)/((y+z)(x+y))) 2(y^2 +yx+zx+zy)=(z+x)(x+2y+z) 2y^2 +2yx+2zx+2zy = zx+2zy+z^2 +x^2 +2xy+xz 2y^2 = x^2 +z^2 ⇒so x^2 , y^2 ,z^2 →AP

$$\left(\mathrm{2}\right)\:\frac{\mathrm{1}}{\mathrm{y}+\mathrm{z}}\:,\:\frac{\mathrm{1}}{\mathrm{z}+\mathrm{x}}\:,\:\frac{\mathrm{1}}{\mathrm{x}+\mathrm{y}}\:\rightarrow\mathrm{AP} \\ $$$$\Rightarrow\frac{\mathrm{2}}{\mathrm{z}+\mathrm{x}}\:=\:\frac{\mathrm{1}}{\mathrm{y}+\mathrm{z}}\:+\:\frac{\mathrm{1}}{\mathrm{x}+\mathrm{y}} \\ $$$$\frac{\mathrm{2}}{\mathrm{z}+\mathrm{x}}\:=\:\frac{\mathrm{x}+\mathrm{2y}+\mathrm{z}}{\left(\mathrm{y}+\mathrm{z}\right)\left(\mathrm{x}+\mathrm{y}\right)} \\ $$$$\mathrm{2}\left(\mathrm{y}^{\mathrm{2}} +\mathrm{yx}+\mathrm{zx}+\mathrm{zy}\right)=\left(\mathrm{z}+\mathrm{x}\right)\left(\mathrm{x}+\mathrm{2y}+\mathrm{z}\right) \\ $$$$\mathrm{2y}^{\mathrm{2}} +\mathrm{2yx}+\mathrm{2zx}+\mathrm{2zy}\:= \\ $$$$\mathrm{zx}+\mathrm{2zy}+\mathrm{z}^{\mathrm{2}} +\mathrm{x}^{\mathrm{2}} +\mathrm{2xy}+\mathrm{xz} \\ $$$$\mathrm{2y}^{\mathrm{2}} =\:\mathrm{x}^{\mathrm{2}} +\mathrm{z}^{\mathrm{2}} \:\Rightarrow\mathrm{so}\:\mathrm{x}^{\mathrm{2}} ,\:\mathrm{y}^{\mathrm{2}} ,\mathrm{z}^{\mathrm{2}} \:\rightarrow\mathrm{AP} \\ $$

Answered by PRITHWISH SEN 2 last updated on 03/Jul/20

∵ a,b and c are the three cosecutive terms of a linear sequence ∴ a+c=2b now a((1/b)+(1/c))+c((1/a)+(1/b)) =((b(a^2 +c^2 )+ac(a+c))/(abc)) =((b(a^2 +c^2 )+2abc)/(abc)) =(((a+c)^2 )/(ac)) = ((2b(a+c))/(ac)) =2b((1/a)+(1/c)) ∴ the terms are also the 3 consecutive terms of the same linear sequence proved

$$\because\:\mathrm{a},\mathrm{b}\:\mathrm{and}\:\mathrm{c}\:\mathrm{are}\:\mathrm{the}\:\mathrm{three}\:\mathrm{cosecutive}\:\mathrm{terms}\:\mathrm{of} \\ $$$$\mathrm{a}\:\boldsymbol{\mathrm{linear}}\:\boldsymbol{\mathrm{sequence}} \\ $$$$\therefore\:\mathrm{a}+\mathrm{c}=\mathrm{2b} \\ $$$$\mathrm{now}\:\mathrm{a}\left(\frac{\mathrm{1}}{\mathrm{b}}+\frac{\mathrm{1}}{\mathrm{c}}\right)+\mathrm{c}\left(\frac{\mathrm{1}}{\mathrm{a}}+\frac{\mathrm{1}}{\mathrm{b}}\right) \\ $$$$=\frac{\mathrm{b}\left(\mathrm{a}^{\mathrm{2}} +\mathrm{c}^{\mathrm{2}} \right)+\mathrm{ac}\left(\mathrm{a}+\mathrm{c}\right)}{\mathrm{abc}} \\ $$$$=\frac{\mathrm{b}\left(\mathrm{a}^{\mathrm{2}} +\mathrm{c}^{\mathrm{2}} \right)+\mathrm{2abc}}{\mathrm{abc}}\:=\frac{\left(\mathrm{a}+\mathrm{c}\right)^{\mathrm{2}} }{\mathrm{ac}}\:=\:\frac{\mathrm{2b}\left(\mathrm{a}+\mathrm{c}\right)}{\mathrm{ac}} \\ $$$$=\mathrm{2b}\left(\frac{\mathrm{1}}{\mathrm{a}}+\frac{\mathrm{1}}{\mathrm{c}}\right) \\ $$$$\therefore\:\mathrm{the}\:\mathrm{terms}\:\mathrm{are}\:\mathrm{also}\:\mathrm{the}\:\mathrm{3}\:\mathrm{consecutive}\:\mathrm{terms}\:\mathrm{of} \\ $$$$\mathrm{the}\:\mathrm{same}\:\mathrm{linear}\:\mathrm{sequence}\:\:\boldsymbol{\mathrm{proved}} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com