Question and Answers Forum

All Questions      Topic List

Relation and Functions Questions

Previous in All Question      Next in All Question      

Previous in Relation and Functions      Next in Relation and Functions      

Question Number 101595 by mathmax by abdo last updated on 03/Jul/20

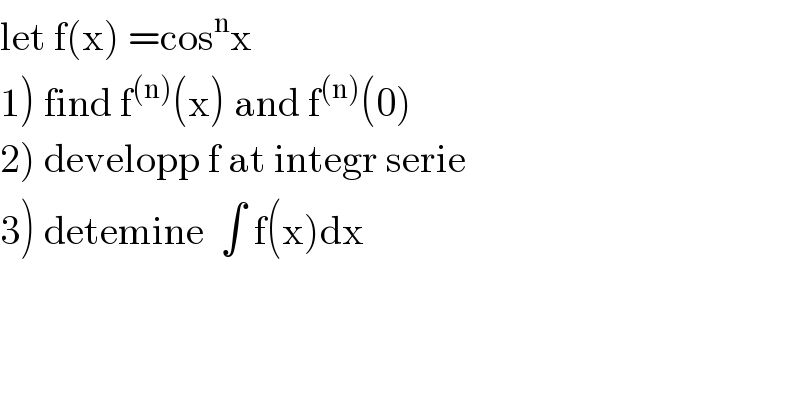
let f(x) =cos^n x 1) find f^((n)) (x) and f^((n)) (0) 2) developp f at integr serie 3) detemine ∫ f(x)dx

$$\mathrm{let}\:\mathrm{f}\left(\mathrm{x}\right)\:=\mathrm{cos}^{\mathrm{n}} \mathrm{x} \\ $$$$\left.\mathrm{1}\right)\:\mathrm{find}\:\mathrm{f}^{\left(\mathrm{n}\right)} \left(\mathrm{x}\right)\:\mathrm{and}\:\mathrm{f}^{\left(\mathrm{n}\right)} \left(\mathrm{0}\right) \\ $$$$\left.\mathrm{2}\right)\:\mathrm{developp}\:\mathrm{f}\:\mathrm{at}\:\mathrm{integr}\:\mathrm{serie} \\ $$$$\left.\mathrm{3}\right)\:\mathrm{detemine}\:\:\int\:\mathrm{f}\left(\mathrm{x}\right)\mathrm{dx} \\ $$

Answered by mathmax by abdo last updated on 05/Jul/20

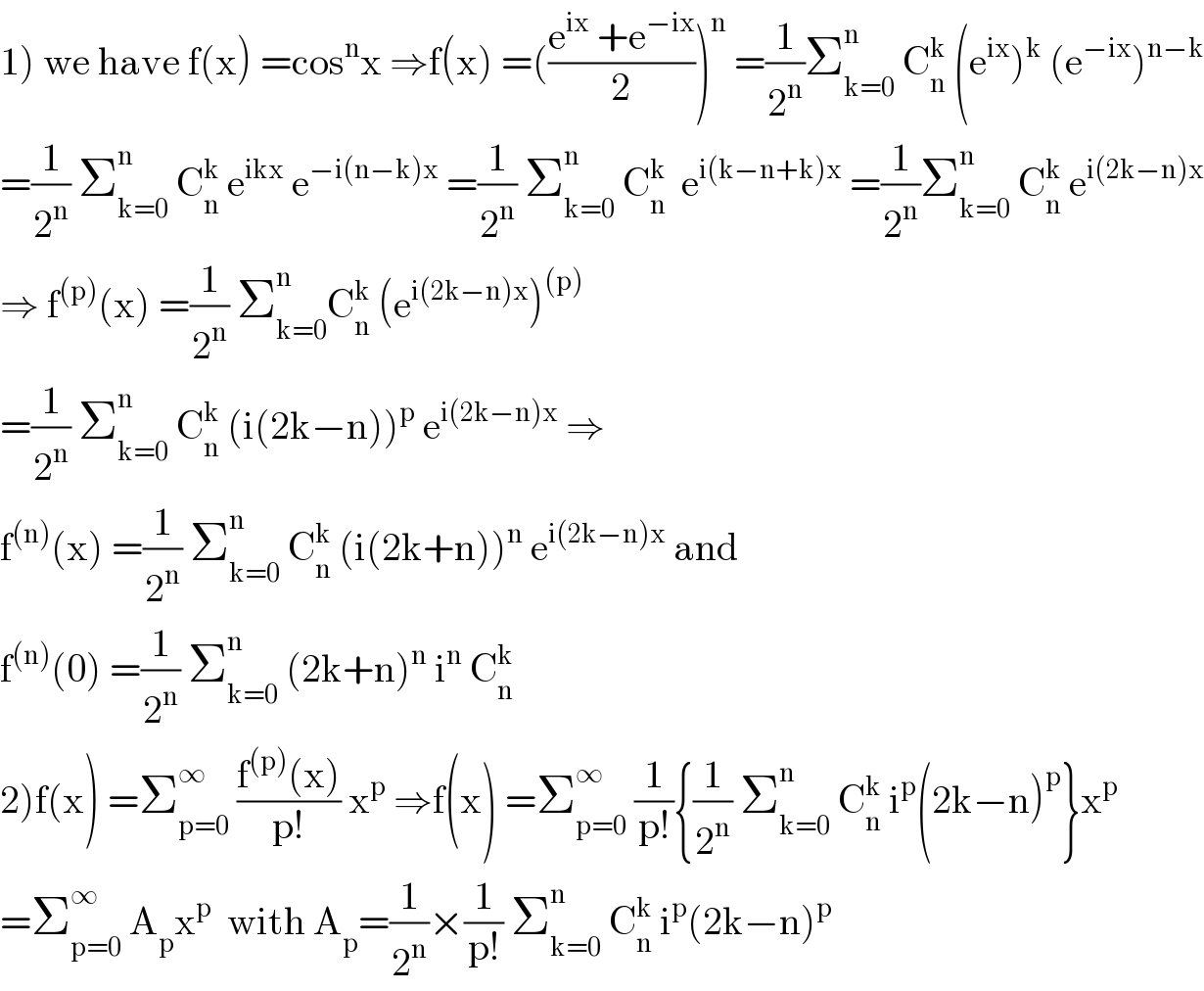
1) we have f(x) =cos^n x ⇒f(x) =(((e^(ix) +e^(−ix) )/2))^n =(1/2^n )Σ_(k=0) ^n C_n ^k (e^(ix) )^k (e^(−ix) )^(n−k) =(1/2^n ) Σ_(k=0) ^n C_n ^k e^(ikx) e^(−i(n−k)x) =(1/2^n ) Σ_(k=0) ^n C_n ^k e^(i(k−n+k)x) =(1/2^n )Σ_(k=0) ^n C_n ^k e^(i(2k−n)x) ⇒ f^((p)) (x) =(1/2^n ) Σ_(k=0) ^n C_n ^k (e^(i(2k−n)x) )^((p)) =(1/2^n ) Σ_(k=0) ^n C_n ^k (i(2k−n))^p e^(i(2k−n)x) ⇒ f^((n)) (x) =(1/2^n ) Σ_(k=0) ^n C_n ^k (i(2k+n))^n e^(i(2k−n)x) and f^((n)) (0) =(1/2^n ) Σ_(k=0) ^n (2k+n)^n i^n C_n ^k 2)f(x) =Σ_(p=0) ^∞ ((f^((p)) (x))/(p!)) x^p ⇒f(x) =Σ_(p=0) ^∞ (1/(p!)){(1/2^n ) Σ_(k=0) ^n C_n ^k i^p (2k−n)^p }x^p =Σ_(p=0) ^∞ A_p x^p with A_p =(1/2^n )×(1/(p!)) Σ_(k=0) ^n C_n ^k i^p (2k−n)^p

$$\left.\mathrm{1}\right)\:\mathrm{we}\:\mathrm{have}\:\mathrm{f}\left(\mathrm{x}\right)\:=\mathrm{cos}^{\mathrm{n}} \mathrm{x}\:\Rightarrow\mathrm{f}\left(\mathrm{x}\right)\:=\left(\frac{\mathrm{e}^{\mathrm{ix}} \:+\mathrm{e}^{−\mathrm{ix}} }{\mathrm{2}}\right)^{\mathrm{n}} \:=\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{n}} }\sum_{\mathrm{k}=\mathrm{0}} ^{\mathrm{n}} \:\mathrm{C}_{\mathrm{n}} ^{\mathrm{k}} \:\left(\mathrm{e}^{\mathrm{ix}} \right)^{\mathrm{k}} \:\left(\mathrm{e}^{−\mathrm{ix}} \right)^{\mathrm{n}−\mathrm{k}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{n}} }\:\sum_{\mathrm{k}=\mathrm{0}} ^{\mathrm{n}} \:\mathrm{C}_{\mathrm{n}} ^{\mathrm{k}} \:\mathrm{e}^{\mathrm{ikx}} \:\mathrm{e}^{−\mathrm{i}\left(\mathrm{n}−\mathrm{k}\right)\mathrm{x}} \:=\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{n}} }\:\sum_{\mathrm{k}=\mathrm{0}} ^{\mathrm{n}} \:\mathrm{C}_{\mathrm{n}} ^{\mathrm{k}} \:\:\mathrm{e}^{\mathrm{i}\left(\mathrm{k}−\mathrm{n}+\mathrm{k}\right)\mathrm{x}} \:=\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{n}} }\sum_{\mathrm{k}=\mathrm{0}} ^{\mathrm{n}} \:\mathrm{C}_{\mathrm{n}} ^{\mathrm{k}} \:\mathrm{e}^{\mathrm{i}\left(\mathrm{2k}−\mathrm{n}\right)\mathrm{x}} \\ $$$$\Rightarrow\:\mathrm{f}^{\left(\mathrm{p}\right)} \left(\mathrm{x}\right)\:=\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{n}} }\:\sum_{\mathrm{k}=\mathrm{0}} ^{\mathrm{n}} \mathrm{C}_{\mathrm{n}} ^{\mathrm{k}} \:\left(\mathrm{e}^{\mathrm{i}\left(\mathrm{2k}−\mathrm{n}\right)\mathrm{x}} \right)^{\left(\mathrm{p}\right)} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{n}} }\:\sum_{\mathrm{k}=\mathrm{0}} ^{\mathrm{n}} \:\mathrm{C}_{\mathrm{n}} ^{\mathrm{k}} \:\left(\mathrm{i}\left(\mathrm{2k}−\mathrm{n}\right)\right)^{\mathrm{p}} \:\mathrm{e}^{\mathrm{i}\left(\mathrm{2k}−\mathrm{n}\right)\mathrm{x}} \:\Rightarrow \\ $$$$\mathrm{f}^{\left(\mathrm{n}\right)} \left(\mathrm{x}\right)\:=\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{n}} }\:\sum_{\mathrm{k}=\mathrm{0}} ^{\mathrm{n}} \:\mathrm{C}_{\mathrm{n}} ^{\mathrm{k}} \:\left(\mathrm{i}\left(\mathrm{2k}+\mathrm{n}\right)\right)^{\mathrm{n}} \:\mathrm{e}^{\mathrm{i}\left(\mathrm{2k}−\mathrm{n}\right)\mathrm{x}} \:\mathrm{and}\: \\ $$$$\mathrm{f}^{\left(\mathrm{n}\right)} \left(\mathrm{0}\right)\:=\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{n}} }\:\sum_{\mathrm{k}=\mathrm{0}} ^{\mathrm{n}} \:\left(\mathrm{2k}+\mathrm{n}\right)^{\mathrm{n}} \:\mathrm{i}^{\mathrm{n}} \:\mathrm{C}_{\mathrm{n}} ^{\mathrm{k}} \\ $$$$\left.\mathrm{2}\right)\mathrm{f}\left(\mathrm{x}\right)\:=\sum_{\mathrm{p}=\mathrm{0}} ^{\infty} \:\frac{\mathrm{f}^{\left(\mathrm{p}\right)} \left(\mathrm{x}\right)}{\mathrm{p}!}\:\mathrm{x}^{\mathrm{p}} \:\Rightarrow\mathrm{f}\left(\mathrm{x}\right)\:=\sum_{\mathrm{p}=\mathrm{0}} ^{\infty} \:\frac{\mathrm{1}}{\mathrm{p}!}\left\{\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{n}} }\:\sum_{\mathrm{k}=\mathrm{0}} ^{\mathrm{n}} \:\mathrm{C}_{\mathrm{n}} ^{\mathrm{k}} \:\mathrm{i}^{\mathrm{p}} \left(\mathrm{2k}−\mathrm{n}\right)^{\mathrm{p}} \right\}\mathrm{x}^{\mathrm{p}} \\ $$$$=\sum_{\mathrm{p}=\mathrm{0}} ^{\infty} \:\mathrm{A}_{\mathrm{p}} \mathrm{x}^{\mathrm{p}} \:\:\mathrm{with}\:\mathrm{A}_{\mathrm{p}} =\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{n}} }×\frac{\mathrm{1}}{\mathrm{p}!}\:\sum_{\mathrm{k}=\mathrm{0}} ^{\mathrm{n}} \:\mathrm{C}_{\mathrm{n}} ^{\mathrm{k}} \:\mathrm{i}^{\mathrm{p}} \left(\mathrm{2k}−\mathrm{n}\right)^{\mathrm{p}} \\ $$

Answered by mathmax by abdo last updated on 05/Jul/20

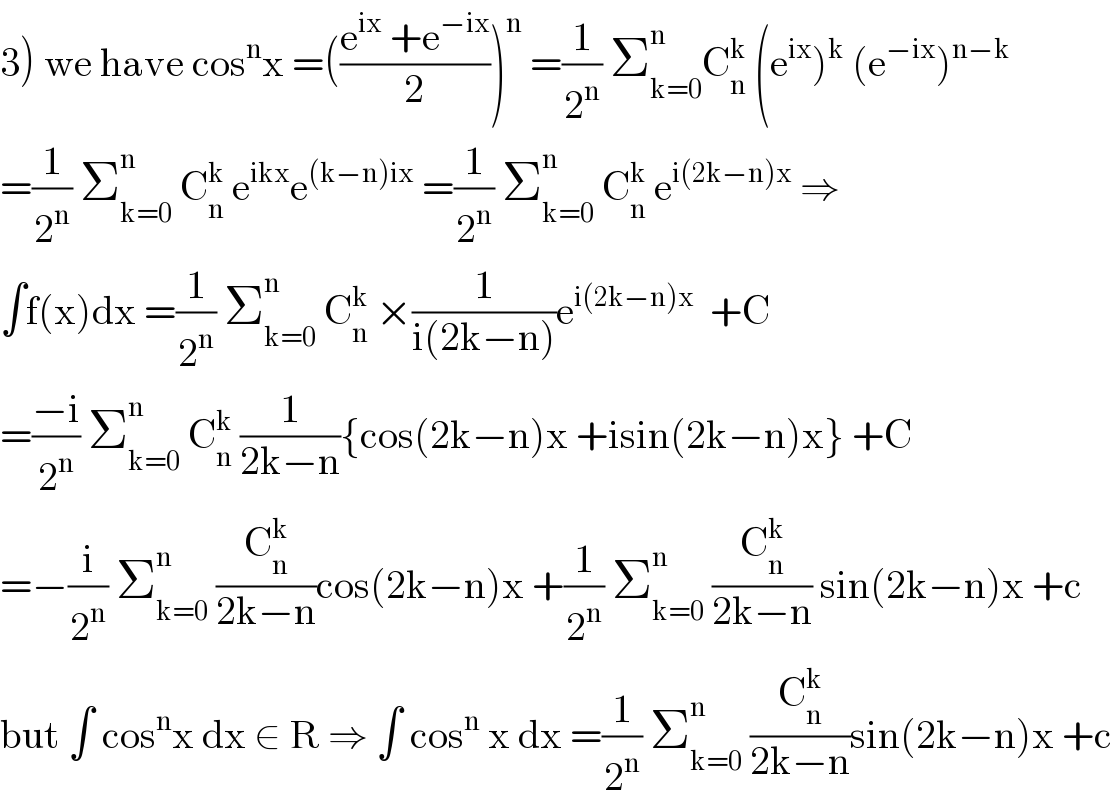
3) we have cos^n x =(((e^(ix) +e^(−ix) )/2))^n =(1/2^n ) Σ_(k=0) ^n C_n ^k (e^(ix) )^k (e^(−ix) )^(n−k) =(1/2^n ) Σ_(k=0) ^n C_n ^k e^(ikx) e^((k−n)ix) =(1/2^n ) Σ_(k=0) ^n C_n ^k e^(i(2k−n)x) ⇒ ∫f(x)dx =(1/2^n ) Σ_(k=0) ^n C_n ^k ×(1/(i(2k−n)))e^(i(2k−n)x) +C =((−i)/2^n ) Σ_(k=0) ^n C_n ^k (1/(2k−n)){cos(2k−n)x +isin(2k−n)x} +C =−(i/2^n ) Σ_(k=0) ^n (C_n ^k /(2k−n))cos(2k−n)x +(1/2^n ) Σ_(k=0) ^n (C_n ^k /(2k−n)) sin(2k−n)x +c but ∫ cos^n x dx ∈ R ⇒ ∫ cos^n x dx =(1/2^n ) Σ_(k=0) ^n (C_n ^k /(2k−n))sin(2k−n)x +c

$$\left.\mathrm{3}\right)\:\mathrm{we}\:\mathrm{have}\:\mathrm{cos}^{\mathrm{n}} \mathrm{x}\:=\left(\frac{\mathrm{e}^{\mathrm{ix}} \:+\mathrm{e}^{−\mathrm{ix}} }{\mathrm{2}}\right)^{\mathrm{n}} \:=\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{n}} }\:\sum_{\mathrm{k}=\mathrm{0}} ^{\mathrm{n}} \mathrm{C}_{\mathrm{n}} ^{\mathrm{k}} \:\left(\mathrm{e}^{\mathrm{ix}} \right)^{\mathrm{k}} \:\left(\mathrm{e}^{−\mathrm{ix}} \right)^{\mathrm{n}−\mathrm{k}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{n}} }\:\sum_{\mathrm{k}=\mathrm{0}} ^{\mathrm{n}} \:\mathrm{C}_{\mathrm{n}} ^{\mathrm{k}} \:\mathrm{e}^{\mathrm{ikx}} \mathrm{e}^{\left(\mathrm{k}−\mathrm{n}\right)\mathrm{ix}} \:=\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{n}} }\:\sum_{\mathrm{k}=\mathrm{0}} ^{\mathrm{n}} \:\mathrm{C}_{\mathrm{n}} ^{\mathrm{k}} \:\mathrm{e}^{\mathrm{i}\left(\mathrm{2k}−\mathrm{n}\right)\mathrm{x}} \:\Rightarrow \\ $$$$\int\mathrm{f}\left(\mathrm{x}\right)\mathrm{dx}\:=\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{n}} }\:\sum_{\mathrm{k}=\mathrm{0}} ^{\mathrm{n}} \:\mathrm{C}_{\mathrm{n}} ^{\mathrm{k}} \:×\frac{\mathrm{1}}{\mathrm{i}\left(\mathrm{2k}−\mathrm{n}\right)}\mathrm{e}^{\mathrm{i}\left(\mathrm{2k}−\mathrm{n}\right)\mathrm{x}} \:\:+\mathrm{C} \\ $$$$=\frac{−\mathrm{i}}{\mathrm{2}^{\mathrm{n}} }\:\sum_{\mathrm{k}=\mathrm{0}} ^{\mathrm{n}} \:\mathrm{C}_{\mathrm{n}} ^{\mathrm{k}} \:\frac{\mathrm{1}}{\mathrm{2k}−\mathrm{n}}\left\{\mathrm{cos}\left(\mathrm{2k}−\mathrm{n}\right)\mathrm{x}\:+\mathrm{isin}\left(\mathrm{2k}−\mathrm{n}\right)\mathrm{x}\right\}\:+\mathrm{C} \\ $$$$=−\frac{\mathrm{i}}{\mathrm{2}^{\mathrm{n}} }\:\sum_{\mathrm{k}=\mathrm{0}} ^{\mathrm{n}} \:\frac{\mathrm{C}_{\mathrm{n}} ^{\mathrm{k}} }{\mathrm{2k}−\mathrm{n}}\mathrm{cos}\left(\mathrm{2k}−\mathrm{n}\right)\mathrm{x}\:+\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{n}} }\:\sum_{\mathrm{k}=\mathrm{0}} ^{\mathrm{n}} \:\frac{\mathrm{C}_{\mathrm{n}} ^{\mathrm{k}} }{\mathrm{2k}−\mathrm{n}}\:\mathrm{sin}\left(\mathrm{2k}−\mathrm{n}\right)\mathrm{x}\:+\mathrm{c} \\ $$$$\mathrm{but}\:\int\:\mathrm{cos}^{\mathrm{n}} \mathrm{x}\:\mathrm{dx}\:\in\:\mathrm{R}\:\Rightarrow\:\int\:\mathrm{cos}^{\mathrm{n}} \:\mathrm{x}\:\mathrm{dx}\:=\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{n}} }\:\sum_{\mathrm{k}=\mathrm{0}} ^{\mathrm{n}} \:\frac{\mathrm{C}_{\mathrm{n}} ^{\mathrm{k}} }{\mathrm{2k}−\mathrm{n}}\mathrm{sin}\left(\mathrm{2k}−\mathrm{n}\right)\mathrm{x}\:+\mathrm{c} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com