Question and Answers Forum

All Questions      Topic List

None Questions

Previous in All Question      Next in All Question      

Previous in None      Next in None      

Question Number 101645 by mathocean1 last updated on 03/Jul/20

E is a vectorial plane in B=(i^→ ,j^→ ) base. f is an endomorphism of E. f(i^→ )=4i^→ −j^→ and f(j^→ )=2i^→ +j^→ . u^→ =xi^→ +yj^→ ∈ E and x,y ∈ R. 1) Determinate f^( −1) (u).

$${E}\:{is}\:{a}\:{vectorial}\:{plane}\:{in}\:{B}=\left(\overset{\rightarrow} {{i}},\overset{\rightarrow} {{j}}\right) \\ $$$${base}.\:{f}\:{is}\:{an}\:{endomorphism}\:{of}\:{E}. \\ $$$${f}\left(\overset{\rightarrow} {{i}}\right)=\mathrm{4}\overset{\rightarrow} {{i}}−\overset{\rightarrow} {{j}}\:{and}\:{f}\left(\overset{\rightarrow} {{j}}\right)=\mathrm{2}\overset{\rightarrow} {{i}}+\overset{\rightarrow} {{j}}. \\ $$$$\overset{\rightarrow} {{u}}={x}\overset{\rightarrow} {{i}}+{y}\overset{\rightarrow} {{j}}\:\in\:{E}\:{and}\:{x},{y}\:\in\:\mathbb{R}. \\ $$$$\left.\mathrm{1}\right)\:{Determinate}\:{f}^{\:−\mathrm{1}} \left({u}\right). \\ $$

Answered by mathmax by abdo last updated on 03/Jul/20

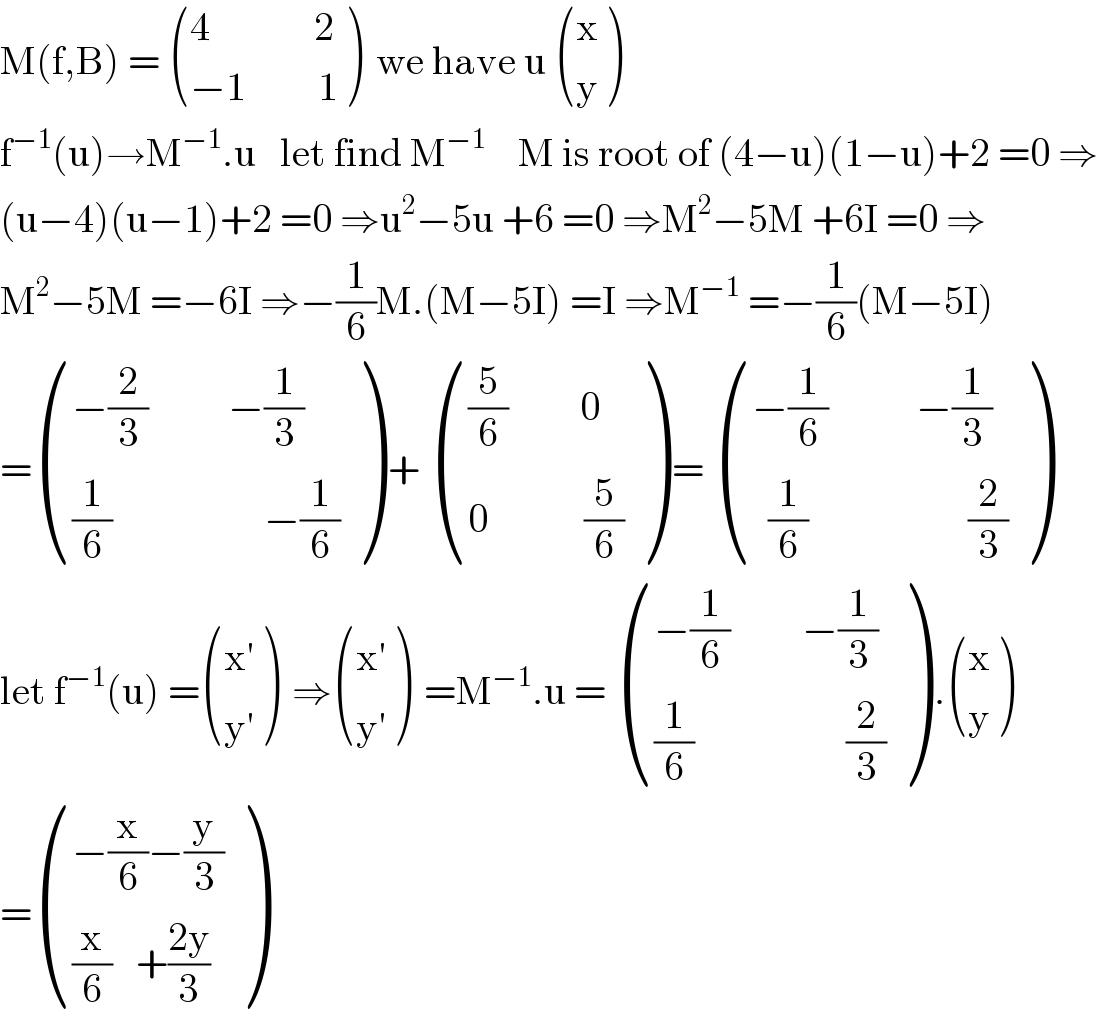
M(f,B) = (((4 2)),((−1 1)) ) we have u ((x),(y) ) f^(−1) (u)→M^(−1) .u let find M^(−1) M is root of (4−u)(1−u)+2 =0 ⇒ (u−4)(u−1)+2 =0 ⇒u^2 −5u +6 =0 ⇒M^2 −5M +6I =0 ⇒ M^2 −5M =−6I ⇒−(1/6)M.(M−5I) =I ⇒M^(−1) =−(1/6)(M−5I) = (((−(2/3) −(1/3))),(((1/6) −(1/6))) ) + ((((5/6) 0)),((0 (5/6))) ) = (((−(1/6) −(1/3))),(( (1/6) (2/3))) ) let f^(−1) (u) = ((x^′ ),(y^′ ) ) ⇒ ((x^′ ),(y^′ ) ) =M^(−1) .u = (((−(1/6) −(1/3))),(((1/6) (2/3))) ) . ((x),(y) ) = (((−(x/6)−(y/3))),(((x/6) +((2y)/3))) )

$$\mathrm{M}\left(\mathrm{f},\mathrm{B}\right)\:=\:\begin{pmatrix}{\mathrm{4}\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{2}}\\{−\mathrm{1}\:\:\:\:\:\:\:\:\:\mathrm{1}}\end{pmatrix}\:\:\mathrm{we}\:\mathrm{have}\:\mathrm{u}\:\begin{pmatrix}{\mathrm{x}}\\{\mathrm{y}}\end{pmatrix} \\ $$$$\mathrm{f}^{−\mathrm{1}} \left(\mathrm{u}\right)\rightarrow\mathrm{M}^{−\mathrm{1}} .\mathrm{u}\:\:\:\mathrm{let}\:\mathrm{find}\:\mathrm{M}^{−\mathrm{1}} \:\:\:\:\mathrm{M}\:\mathrm{is}\:\mathrm{root}\:\mathrm{of}\:\left(\mathrm{4}−\mathrm{u}\right)\left(\mathrm{1}−\mathrm{u}\right)+\mathrm{2}\:=\mathrm{0}\:\Rightarrow \\ $$$$\left(\mathrm{u}−\mathrm{4}\right)\left(\mathrm{u}−\mathrm{1}\right)+\mathrm{2}\:=\mathrm{0}\:\Rightarrow\mathrm{u}^{\mathrm{2}} −\mathrm{5u}\:+\mathrm{6}\:=\mathrm{0}\:\Rightarrow\mathrm{M}^{\mathrm{2}} −\mathrm{5M}\:+\mathrm{6I}\:=\mathrm{0}\:\Rightarrow \\ $$$$\mathrm{M}^{\mathrm{2}} −\mathrm{5M}\:=−\mathrm{6I}\:\Rightarrow−\frac{\mathrm{1}}{\mathrm{6}}\mathrm{M}.\left(\mathrm{M}−\mathrm{5I}\right)\:=\mathrm{I}\:\Rightarrow\mathrm{M}^{−\mathrm{1}} \:=−\frac{\mathrm{1}}{\mathrm{6}}\left(\mathrm{M}−\mathrm{5I}\right) \\ $$$$=\begin{pmatrix}{−\frac{\mathrm{2}}{\mathrm{3}}\:\:\:\:\:\:\:\:\:\:−\frac{\mathrm{1}}{\mathrm{3}}}\\{\frac{\mathrm{1}}{\mathrm{6}}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:−\frac{\mathrm{1}}{\mathrm{6}}}\end{pmatrix}\:+\:\begin{pmatrix}{\frac{\mathrm{5}}{\mathrm{6}}\:\:\:\:\:\:\:\:\:\mathrm{0}}\\{\mathrm{0}\:\:\:\:\:\:\:\:\:\:\:\:\frac{\mathrm{5}}{\mathrm{6}}}\end{pmatrix}\:=\:\begin{pmatrix}{−\frac{\mathrm{1}}{\mathrm{6}}\:\:\:\:\:\:\:\:\:\:\:−\frac{\mathrm{1}}{\mathrm{3}}}\\{\:\:\frac{\mathrm{1}}{\mathrm{6}}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\frac{\mathrm{2}}{\mathrm{3}}}\end{pmatrix} \\ $$$$\mathrm{let}\:\mathrm{f}^{−\mathrm{1}} \left(\mathrm{u}\right)\:=\begin{pmatrix}{\mathrm{x}^{'} }\\{\mathrm{y}^{'} }\end{pmatrix}\:\:\Rightarrow\begin{pmatrix}{\mathrm{x}^{'} }\\{\mathrm{y}^{'} }\end{pmatrix}\:\:=\mathrm{M}^{−\mathrm{1}} .\mathrm{u}\:=\:\begin{pmatrix}{−\frac{\mathrm{1}}{\mathrm{6}}\:\:\:\:\:\:\:\:\:−\frac{\mathrm{1}}{\mathrm{3}}}\\{\frac{\mathrm{1}}{\mathrm{6}}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\frac{\mathrm{2}}{\mathrm{3}}}\end{pmatrix}\:.\begin{pmatrix}{\mathrm{x}}\\{\mathrm{y}}\end{pmatrix} \\ $$$$=\begin{pmatrix}{−\frac{\mathrm{x}}{\mathrm{6}}−\frac{\mathrm{y}}{\mathrm{3}}}\\{\frac{\mathrm{x}}{\mathrm{6}}\:\:\:+\frac{\mathrm{2y}}{\mathrm{3}}}\end{pmatrix} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com