
Question Number 101650 by I want to learn more last updated on 03/Jul/20
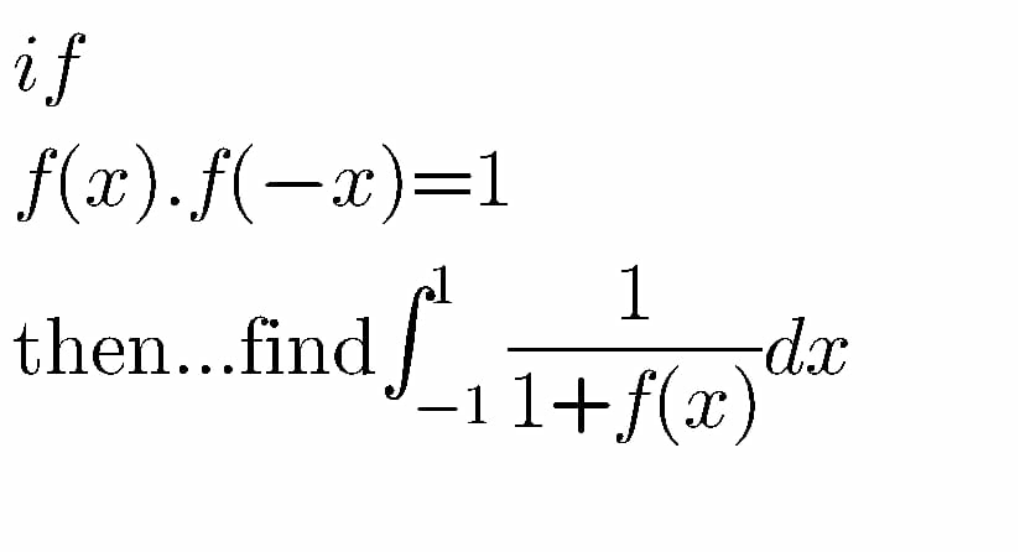
Commented by mr W last updated on 03/Jul/20
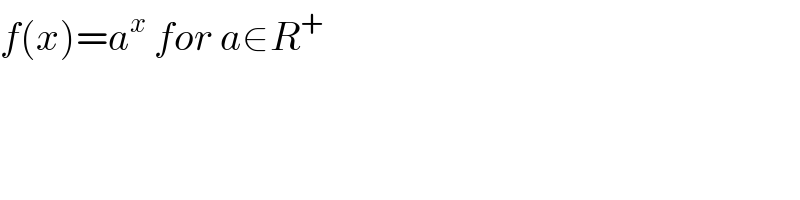
$${f}\left({x}\right)={a}^{{x}} \:{for}\:{a}\in{R}^{+} \\ $$
Answered by mathmax by abdo last updated on 03/Jul/20
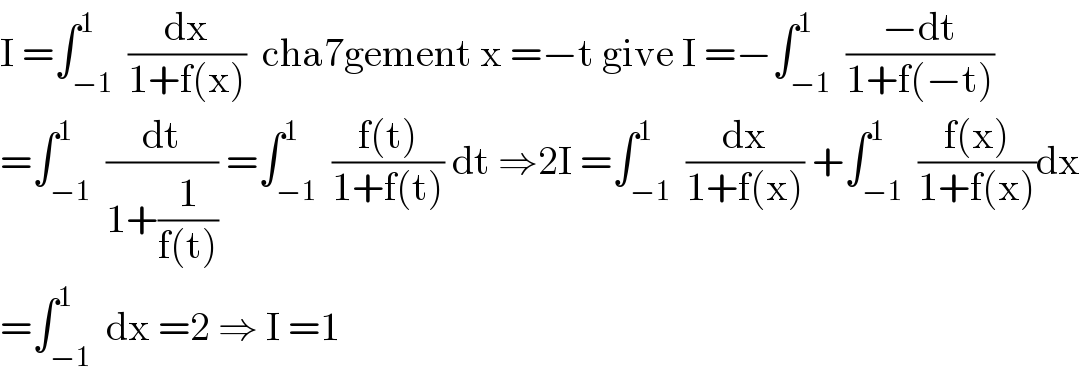
$$\mathrm{I}\:=\int_{−\mathrm{1}} ^{\mathrm{1}} \:\frac{\mathrm{dx}}{\mathrm{1}+\mathrm{f}\left(\mathrm{x}\right)}\:\:\mathrm{cha7gement}\:\mathrm{x}\:=−\mathrm{t}\:\mathrm{give}\:\mathrm{I}\:=−\int_{−\mathrm{1}} ^{\mathrm{1}} \:\frac{−\mathrm{dt}}{\mathrm{1}+\mathrm{f}\left(−\mathrm{t}\right)} \\ $$$$=\int_{−\mathrm{1}} ^{\mathrm{1}} \:\frac{\mathrm{dt}}{\mathrm{1}+\frac{\mathrm{1}}{\mathrm{f}\left(\mathrm{t}\right)}}\:=\int_{−\mathrm{1}} ^{\mathrm{1}} \:\frac{\mathrm{f}\left(\mathrm{t}\right)}{\mathrm{1}+\mathrm{f}\left(\mathrm{t}\right)}\:\mathrm{dt}\:\Rightarrow\mathrm{2I}\:=\int_{−\mathrm{1}} ^{\mathrm{1}} \:\frac{\mathrm{dx}}{\mathrm{1}+\mathrm{f}\left(\mathrm{x}\right)}\:+\int_{−\mathrm{1}} ^{\mathrm{1}} \:\frac{\mathrm{f}\left(\mathrm{x}\right)}{\mathrm{1}+\mathrm{f}\left(\mathrm{x}\right)}\mathrm{dx} \\ $$$$=\int_{−\mathrm{1}} ^{\mathrm{1}} \:\mathrm{dx}\:=\mathrm{2}\:\Rightarrow\:\mathrm{I}\:=\mathrm{1} \\ $$
Commented by I want to learn more last updated on 04/Jul/20

$$\mathrm{Thanks}\:\mathrm{sir} \\ $$
Commented by mathmax by abdo last updated on 04/Jul/20

$$\mathrm{you}\:\mathrm{are}\:\mathrm{welcome} \\ $$
Answered by MAB last updated on 03/Jul/20
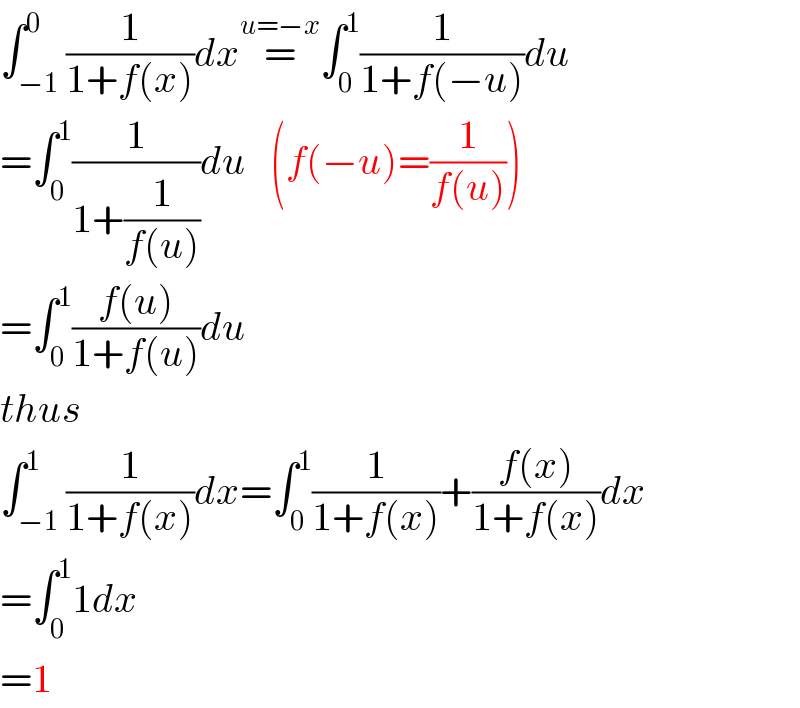
$$\int_{−\mathrm{1}} ^{\mathrm{0}} \frac{\mathrm{1}}{\mathrm{1}+{f}\left({x}\right)}{dx}\overset{{u}=−{x}} {=}\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{1}}{\mathrm{1}+{f}\left(−{u}\right)}{du} \\ $$$$=\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{1}}{\mathrm{1}+\frac{\mathrm{1}}{{f}\left({u}\right)}}{du}\:\:\:\left({f}\left(−{u}\right)=\frac{\mathrm{1}}{{f}\left({u}\right)}\right) \\ $$$$=\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{f}\left({u}\right)}{\mathrm{1}+{f}\left({u}\right)}{du} \\ $$$${thus} \\ $$$$\int_{−\mathrm{1}} ^{\mathrm{1}} \frac{\mathrm{1}}{\mathrm{1}+{f}\left({x}\right)}{dx}=\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{1}}{\mathrm{1}+{f}\left({x}\right)}+\frac{{f}\left({x}\right)}{\mathrm{1}+{f}\left({x}\right)}{dx} \\ $$$$=\int_{\mathrm{0}} ^{\mathrm{1}} \mathrm{1}{dx} \\ $$$$=\mathrm{1} \\ $$
Commented by MAB last updated on 05/Jul/20

$${you}\:{are}\:{welcome} \\ $$
Commented by mr W last updated on 03/Jul/20
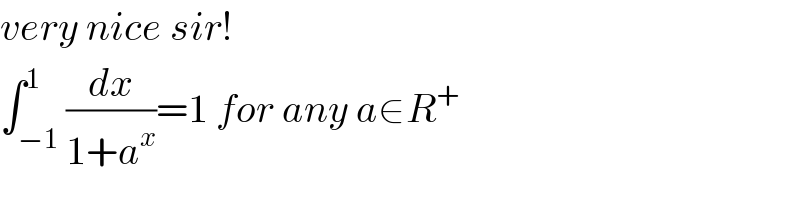
$${very}\:{nice}\:{sir}! \\ $$$$\int_{−\mathrm{1}} ^{\mathrm{1}} \frac{{dx}}{\mathrm{1}+{a}^{{x}} }=\mathrm{1}\:{for}\:{any}\:{a}\in{R}^{+} \\ $$
Commented by I want to learn more last updated on 04/Jul/20

$$\mathrm{Thanks}\:\mathrm{sir}. \\ $$
