Question Number 101658 by mathocean1 last updated on 03/Jul/20

solve in R x^3 −4x−1=0

Answered by 1549442205 last updated on 04/Jul/20

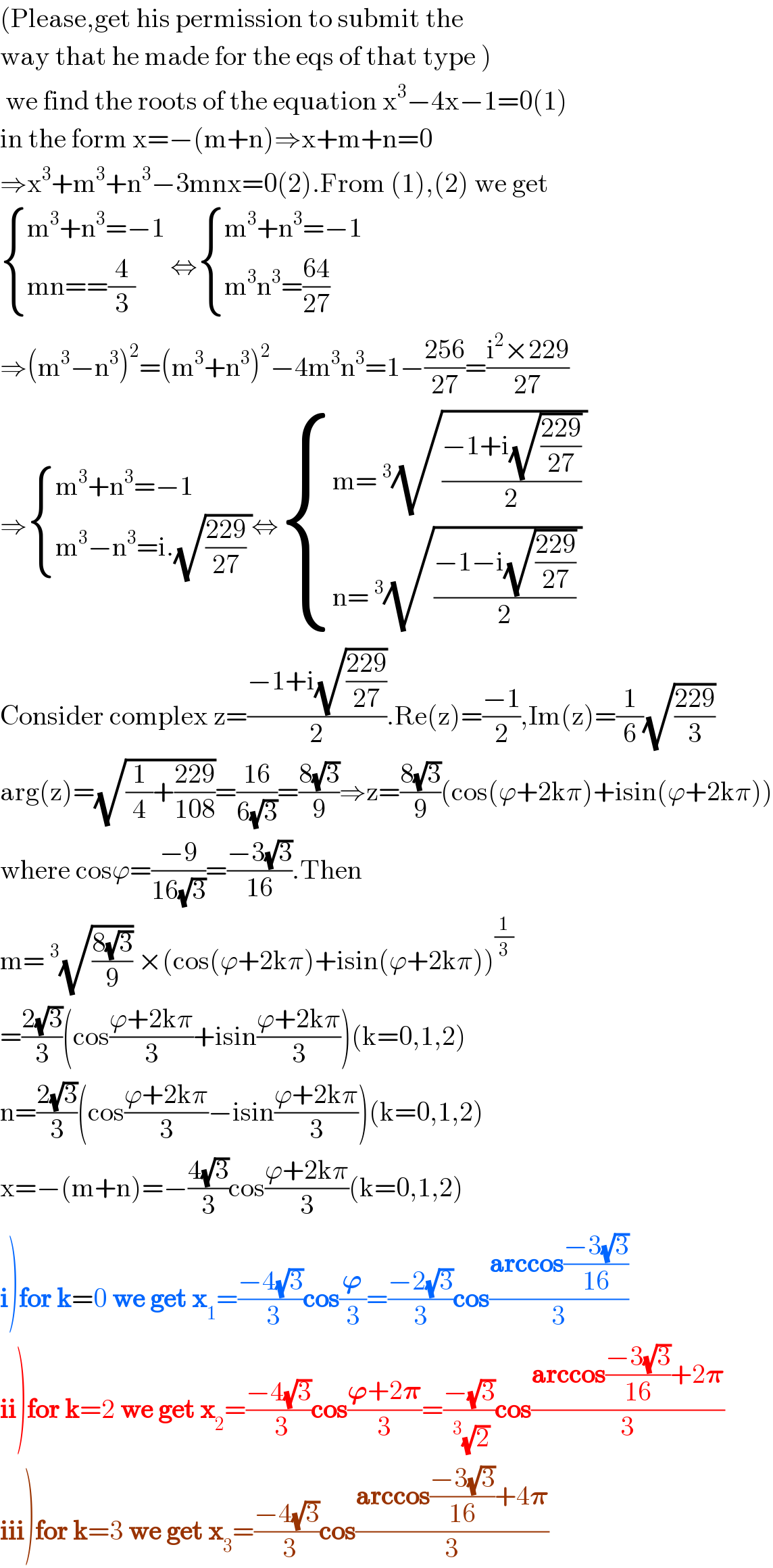
(Please,get his permission to submit the way that he made for the eqs of that type ) we find the roots of the equation x^3 −4x−1=0(1) in the form x=−(m+n)⇒x+m+n=0 ⇒x^3 +m^3 +n^3 −3mnx=0(2).From (1),(2) we get { ((m^3 +n^3 =−1)),((mn==(4/3))) :} ⇔ { ((m^3 +n^3 =−1)),((m^3 n^3 =((64)/(27)))) :} ⇒(m^3 −n^3 )^2 =(m^3 +n^3 )^2 −4m^3 n^3 =1−((256)/(27))=((i^2 ×229)/(27)) ⇒ { ((m^3 +n^3 =−1)),((m^3 −n^3 =i.(√(((229)/(27)) )))) :}⇔ { ((m= ^3 (√(((−1+i(√((229)/(27))))/2) )))),((n= ^3 (√(((−1−i(√((229)/(27))))/2) )))) :} Consider complex z=((−1+i(√((229)/(27))))/2).Re(z)=((−1)/2),Im(z)=(1/6)(√((229)/3)) arg(z)=(√((1/4)+((229)/(108))))=((16)/(6(√3)))=((8(√3))/9)⇒z=((8(√3))/9)(cos(ϕ+2kπ)+isin(ϕ+2kπ)) where cosϕ=((−9)/(16(√3)))=((−3(√3))/(16)).Then m= ^3 (√((8(√3))/9)) ×(cos(ϕ+2kπ)+isin(ϕ+2kπ))^(1/3) =((2(√3))/3)(cos((ϕ+2kπ)/3)+isin((ϕ+2kπ)/3))(k=0,1,2) n=((2(√3))/3)(cos((ϕ+2kπ)/3)−isin((ϕ+2kπ)/3))(k=0,1,2) x=−(m+n)=−((4(√3))/3)cos((ϕ+2kπ)/3)(k=0,1,2) i)for k=0 we get x_1 =((−4(√3))/( 3))cos(𝛟/3)=((−2(√3))/3)cos((arccos((−3(√3))/(16)))/3) ii)for k=2 we get x_2 =((−4(√3))/( 3))cos((𝛟+2𝛑)/3)=((−(√3))/( ^3 (√2)))cos((arccos((−3(√3))/(16))+2𝛑)/3) iii)for k=3 we get x_3 =((−4(√3))/( 3))cos((arccos((−3(√3))/(16))+4𝛑)/3)

Commented by1549442205 last updated on 07/Jul/20

Great,thank you Sir.