Question and Answers Forum

All Questions      Topic List

Differential Equation Questions

Previous in All Question      Next in All Question      

Previous in Differential Equation      Next in Differential Equation      

Question Number 101680 by john santu last updated on 04/Jul/20

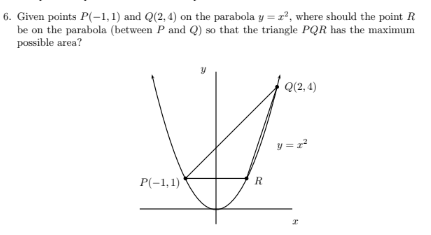
Answered by bemath last updated on 04/Jul/20

let point R(x,x^2 ) area of ΔPQR =(1/2) determinant ((( 2 4 1)),((−1 1 1)),(( x x^2 1))) A(x) =(1/2){2(1−x^2 )−4(−1−x)+1(−x^2 −x)} A(x)=(1/2){2−2x^2 +4+4x−x^2 −x} A(x)= (1/2){−3x^2 +3x+6} ⇔((dA(x))/dx) = (1/2){−6x+3} = 0 , x = (1/2) ⇔ ((d^2 A(x))/dx^2 ) = −6 < 0 ⇐ has max value area triangle PQR has maximum where the point R((1/2),(1/4)) then maximum area is (1/2){((−3)/4) +(3/2)+6} = (1/2){6+(3/4)}= ((27)/8) ★

$$\mathrm{let}\:\mathrm{point}\:\mathrm{R}\left(\mathrm{x},\mathrm{x}^{\mathrm{2}} \right) \\ $$$$\mathrm{area}\:\mathrm{of}\:\Delta\mathrm{PQR}\:=\frac{\mathrm{1}}{\mathrm{2}}\:\begin{vmatrix}{\:\:\:\mathrm{2}\:\:\:\:\mathrm{4}\:\:\:\:\mathrm{1}}\\{−\mathrm{1}\:\:\:\mathrm{1}\:\:\:\mathrm{1}}\\{\:\:\:\mathrm{x}\:\:\:\:\mathrm{x}^{\mathrm{2}} \:\:\mathrm{1}}\end{vmatrix} \\ $$$$\mathrm{A}\left(\mathrm{x}\right)\:=\frac{\mathrm{1}}{\mathrm{2}}\left\{\mathrm{2}\left(\mathrm{1}−\mathrm{x}^{\mathrm{2}} \right)−\mathrm{4}\left(−\mathrm{1}−\mathrm{x}\right)+\mathrm{1}\left(−\mathrm{x}^{\mathrm{2}} −\mathrm{x}\right)\right\} \\ $$$$\mathrm{A}\left(\mathrm{x}\right)=\frac{\mathrm{1}}{\mathrm{2}}\left\{\mathrm{2}−\mathrm{2x}^{\mathrm{2}} +\mathrm{4}+\mathrm{4x}−\mathrm{x}^{\mathrm{2}} −\mathrm{x}\right\} \\ $$$$\mathrm{A}\left(\mathrm{x}\right)=\:\frac{\mathrm{1}}{\mathrm{2}}\left\{−\mathrm{3x}^{\mathrm{2}} +\mathrm{3x}+\mathrm{6}\right\} \\ $$$$\Leftrightarrow\frac{\mathrm{dA}\left(\mathrm{x}\right)}{\mathrm{dx}}\:=\:\frac{\mathrm{1}}{\mathrm{2}}\left\{−\mathrm{6x}+\mathrm{3}\right\}\:=\:\mathrm{0}\:,\:\mathrm{x}\:=\:\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\Leftrightarrow\:\frac{\mathrm{d}^{\mathrm{2}} \mathrm{A}\left(\mathrm{x}\right)}{\mathrm{dx}^{\mathrm{2}} }\:=\:−\mathrm{6}\:<\:\mathrm{0}\:\Leftarrow\:\mathrm{has}\:\mathrm{max}\:\mathrm{value} \\ $$$$\mathrm{area}\:\mathrm{triangle}\:\mathrm{PQR}\:\mathrm{has}\:\mathrm{maximum} \\ $$$$\mathrm{where}\:\mathrm{the}\:\mathrm{point}\:\mathrm{R}\left(\frac{\mathrm{1}}{\mathrm{2}},\frac{\mathrm{1}}{\mathrm{4}}\right)\:\mathrm{then} \\ $$$$\mathrm{maximum}\:\mathrm{area}\:\mathrm{is}\:\frac{\mathrm{1}}{\mathrm{2}}\left\{\frac{−\mathrm{3}}{\mathrm{4}}\:+\frac{\mathrm{3}}{\mathrm{2}}+\mathrm{6}\right\}\:=\:\frac{\mathrm{1}}{\mathrm{2}}\left\{\mathrm{6}+\frac{\mathrm{3}}{\mathrm{4}}\right\}=\:\frac{\mathrm{27}}{\mathrm{8}}\:\bigstar \\ $$

Commented by john santu last updated on 04/Jul/20

correct .

$${correct}\:. \\ $$

Answered by mr W last updated on 04/Jul/20

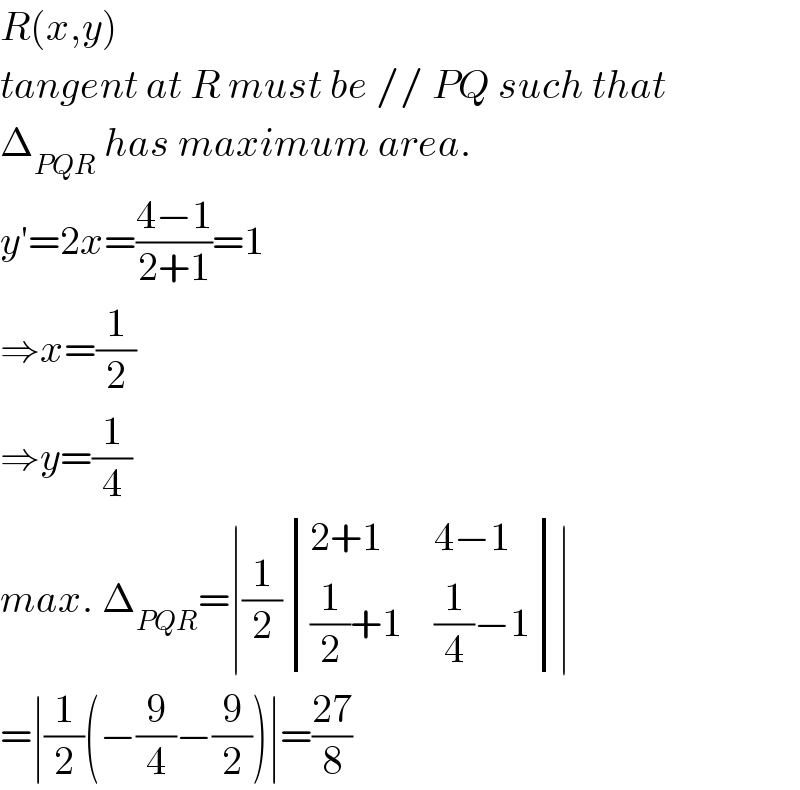
R(x,y) tangent at R must be // PQ such that Δ_(PQR) has maximum area. y′=2x=((4−1)/(2+1))=1 ⇒x=(1/2) ⇒y=(1/4) max. Δ_(PQR) =∣(1/2) determinant (((2+1),(4−1)),(((1/2)+1),((1/4)−1)))∣ =∣(1/2)(−(9/4)−(9/2))∣=((27)/8)

$${R}\left({x},{y}\right) \\ $$$${tangent}\:{at}\:{R}\:{must}\:{be}\://\:{PQ}\:{such}\:{that} \\ $$$$\Delta_{{PQR}} \:{has}\:{maximum}\:{area}. \\ $$$${y}'=\mathrm{2}{x}=\frac{\mathrm{4}−\mathrm{1}}{\mathrm{2}+\mathrm{1}}=\mathrm{1} \\ $$$$\Rightarrow{x}=\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\Rightarrow{y}=\frac{\mathrm{1}}{\mathrm{4}} \\ $$$${max}.\:\Delta_{{PQR}} =\mid\frac{\mathrm{1}}{\mathrm{2}}\begin{vmatrix}{\mathrm{2}+\mathrm{1}}&{\mathrm{4}−\mathrm{1}}\\{\frac{\mathrm{1}}{\mathrm{2}}+\mathrm{1}}&{\frac{\mathrm{1}}{\mathrm{4}}−\mathrm{1}}\end{vmatrix}\mid \\ $$$$=\mid\frac{\mathrm{1}}{\mathrm{2}}\left(−\frac{\mathrm{9}}{\mathrm{4}}−\frac{\mathrm{9}}{\mathrm{2}}\right)\mid=\frac{\mathrm{27}}{\mathrm{8}} \\ $$

Commented by bemath last updated on 04/Jul/20

sir how to proof tangent at R must be paralell to PQ?

$$\mathrm{sir}\:\mathrm{how}\:\mathrm{to}\:\mathrm{proof}\:\mathrm{tangent}\:\mathrm{at}\:\mathrm{R}\: \\ $$$$\mathrm{must}\:\mathrm{be}\:\mathrm{paralell}\:\mathrm{to}\:\mathrm{PQ}? \\ $$

Commented by mr W last updated on 04/Jul/20

base PQ is given. maximum area means then maximum altitude from R to base PQ, i.e. R must have the largest distance to PQ. this is the case when the line through R and parallel to PQ tangents the curve.

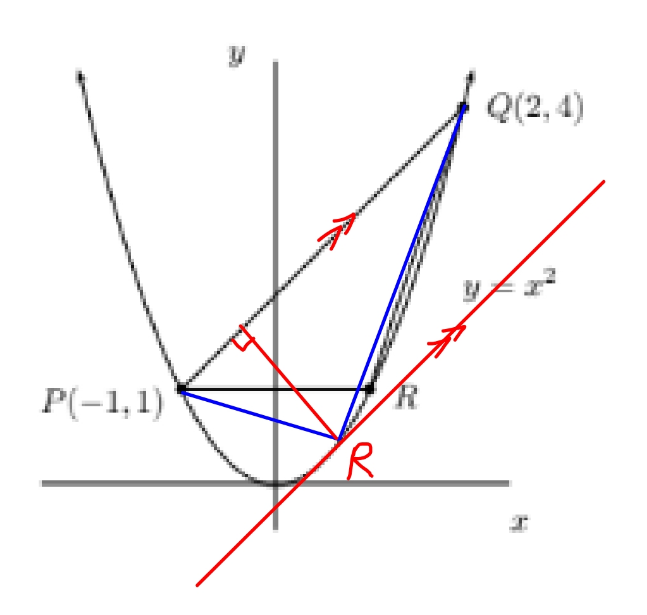
$${base}\:{PQ}\:{is}\:{given}. \\ $$$${maximum}\:{area}\:{means}\:{then}\:{maximum} \\ $$$${altitude}\:{from}\:{R}\:{to}\:{base}\:{PQ},\:{i}.{e}.\:{R} \\ $$$${must}\:{have}\:{the}\:{largest}\:{distance}\:{to}\:{PQ}. \\ $$$${this}\:{is}\:{the}\:{case}\:{when}\:{the}\:{line}\:{through} \\ $$$${R}\:{and}\:{parallel}\:{to}\:{PQ}\:{tangents}\:{the} \\ $$$${curve}. \\ $$

Commented by mr W last updated on 04/Jul/20

Commented by bemath last updated on 04/Jul/20

ok sir. i understand. thank you

$$\mathrm{ok}\:\mathrm{sir}.\:\mathrm{i}\:\mathrm{understand}.\:\mathrm{thank}\:\mathrm{you} \\ $$

Commented by john santu last updated on 04/Jul/20

great

$${great} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com