
Question Number 10169 by Joel575 last updated on 28/Jan/17

$$\frac{\mathrm{2013}}{\mathrm{1}}\:+\:\frac{\mathrm{2013}}{\mathrm{1}+\mathrm{2}}\:+\:\frac{\mathrm{2013}}{\mathrm{1}+\mathrm{2}+\mathrm{3}}\:+\:...\:+\:\frac{\mathrm{2013}}{\mathrm{1}+\mathrm{2}+\mathrm{3}+...+\mathrm{2012}}\:=\:? \\ $$
Answered by prakash jain last updated on 29/Jan/17
![Σ_(i=1) ^(2012) ((2013)/(Σ_(j=1) ^i j)) = 2013Σ_(i=1) ^(2012) (1/(i(i+1)/2)) =2013Σ_(i=1) ^(2012) (2/(i(i+1)))=2013×2Σ_(i=1) ^(2012) ((1/i)−(1/(i+1))) =4026[(1/1)−(1/2)+(1/2)−(1/3)+.....−(1/(2012))+(1/(2012))−(1/(2013))] =4026[1−(1/(2013))]=((4026×2012)/(2013))=2×2012](Q10178.png)
$$\underset{{i}=\mathrm{1}} {\overset{\mathrm{2012}} {\sum}}\:\frac{\mathrm{2013}}{\underset{{j}=\mathrm{1}} {\overset{{i}} {\sum}}{j}}\:=\:\:\mathrm{2013}\underset{{i}=\mathrm{1}} {\overset{\mathrm{2012}} {\sum}}\frac{\mathrm{1}}{{i}\left({i}+\mathrm{1}\right)/\mathrm{2}} \\ $$$$=\mathrm{2013}\underset{{i}=\mathrm{1}} {\overset{\mathrm{2012}} {\sum}}\frac{\mathrm{2}}{{i}\left({i}+\mathrm{1}\right)}=\mathrm{2013}×\mathrm{2}\underset{{i}=\mathrm{1}} {\overset{\mathrm{2012}} {\sum}}\left(\frac{\mathrm{1}}{{i}}−\frac{\mathrm{1}}{{i}+\mathrm{1}}\right) \\ $$$$=\mathrm{4026}\left[\frac{\mathrm{1}}{\mathrm{1}}−\frac{\mathrm{1}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{2}}−\frac{\mathrm{1}}{\mathrm{3}}+.....−\frac{\mathrm{1}}{\mathrm{2012}}+\frac{\mathrm{1}}{\mathrm{2012}}−\frac{\mathrm{1}}{\mathrm{2013}}\right] \\ $$$$=\mathrm{4026}\left[\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2013}}\right]=\frac{\mathrm{4026}×\mathrm{2012}}{\mathrm{2013}}=\mathrm{2}×\mathrm{2012} \\ $$
Commented by mrW1 last updated on 28/Jan/17
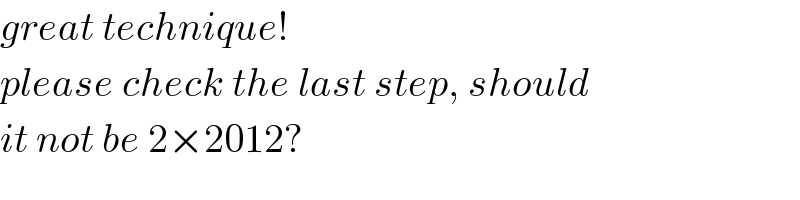
$${great}\:{technique}! \\ $$$${please}\:{check}\:{the}\:{last}\:{step},\:{should} \\ $$$${it}\:{not}\:{be}\:\mathrm{2}×\mathrm{2012}? \\ $$
Commented by prakash jain last updated on 29/Jan/17

$$\mathrm{You}\:\mathrm{are}\:\mathrm{correct}.\:\mathrm{Fixed}\:\mathrm{it}. \\ $$
