Question and Answers Forum

All Questions      Topic List

Trigonometry Questions

Previous in All Question      Next in All Question      

Previous in Trigonometry      Next in Trigonometry      

Question Number 101713 by I want to learn more last updated on 04/Jul/20

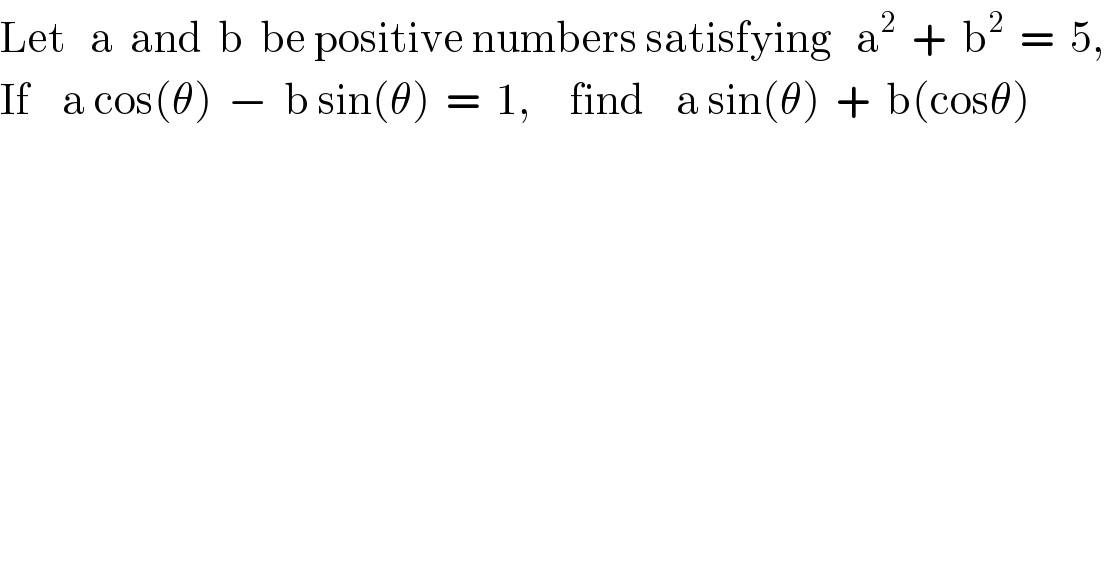
Let a and b be positive numbers satisfying a^2 + b^2 = 5, If a cos(θ) − b sin(θ) = 1, find a sin(θ) + b(cosθ)

$$\mathrm{Let}\:\:\:\mathrm{a}\:\:\mathrm{and}\:\:\mathrm{b}\:\:\mathrm{be}\:\mathrm{positive}\:\mathrm{numbers}\:\mathrm{satisfying}\:\:\:\mathrm{a}^{\mathrm{2}} \:\:+\:\:\mathrm{b}^{\mathrm{2}} \:\:=\:\:\mathrm{5}, \\ $$$$\mathrm{If}\:\:\:\:\mathrm{a}\:\mathrm{cos}\left(\theta\right)\:\:−\:\:\mathrm{b}\:\mathrm{sin}\left(\theta\right)\:\:=\:\:\mathrm{1},\:\:\:\:\:\mathrm{find}\:\:\:\:\mathrm{a}\:\mathrm{sin}\left(\theta\right)\:\:+\:\:\mathrm{b}\left(\mathrm{cos}\theta\right) \\ $$

Answered by mr W last updated on 04/Jul/20

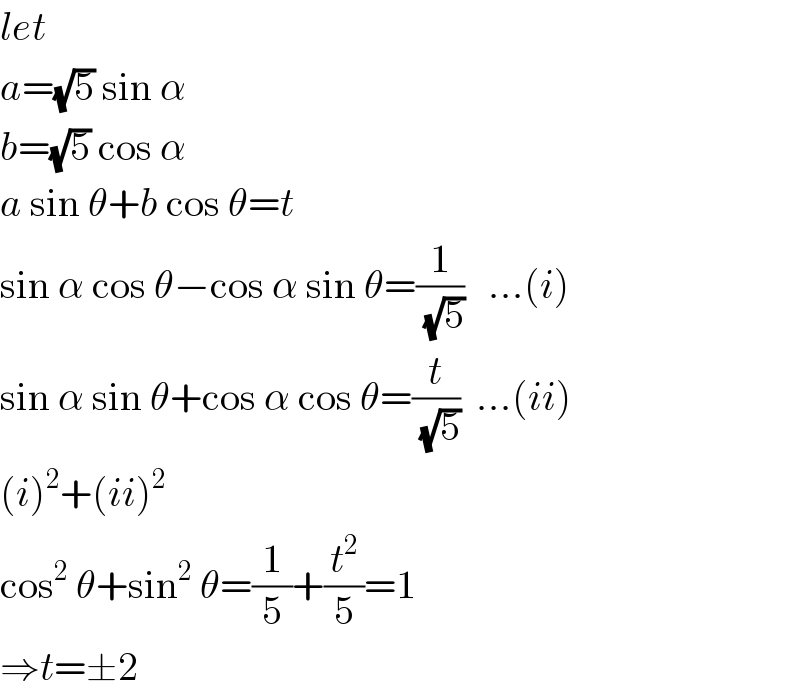
let a=(√5) sin α b=(√5) cos α a sin θ+b cos θ=t sin α cos θ−cos α sin θ=(1/(√5)) ...(i) sin α sin θ+cos α cos θ=(t/(√5)) ...(ii) (i)^2 +(ii)^2 cos^2 θ+sin^2 θ=(1/5)+(t^2 /5)=1 ⇒t=±2

$${let} \\ $$$${a}=\sqrt{\mathrm{5}}\:\mathrm{sin}\:\alpha \\ $$$${b}=\sqrt{\mathrm{5}}\:\mathrm{cos}\:\alpha \\ $$$${a}\:\mathrm{sin}\:\theta+{b}\:\mathrm{cos}\:\theta={t} \\ $$$$\mathrm{sin}\:\alpha\:\mathrm{cos}\:\theta−\mathrm{cos}\:\alpha\:\mathrm{sin}\:\theta=\frac{\mathrm{1}}{\sqrt{\mathrm{5}}}\:\:\:...\left({i}\right) \\ $$$$\mathrm{sin}\:\alpha\:\mathrm{sin}\:\theta+\mathrm{cos}\:\alpha\:\mathrm{cos}\:\theta=\frac{{t}}{\sqrt{\mathrm{5}}}\:\:...\left({ii}\right) \\ $$$$\left({i}\right)^{\mathrm{2}} +\left({ii}\right)^{\mathrm{2}} \\ $$$$\mathrm{cos}^{\mathrm{2}} \:\theta+\mathrm{sin}^{\mathrm{2}} \:\theta=\frac{\mathrm{1}}{\mathrm{5}}+\frac{{t}^{\mathrm{2}} }{\mathrm{5}}=\mathrm{1} \\ $$$$\Rightarrow{t}=\pm\mathrm{2} \\ $$

Commented by I want to learn more last updated on 04/Jul/20

Thanks sir

$$\mathrm{Thanks}\:\mathrm{sir} \\ $$

Answered by Dwaipayan Shikari last updated on 04/Jul/20

a^2 +b^2 =1+x^2 x=±2

$${a}^{\mathrm{2}} +{b}^{\mathrm{2}} =\mathrm{1}+{x}^{\mathrm{2}} \\ $$$${x}=\pm\mathrm{2} \\ $$

Commented by Dwaipayan Shikari last updated on 04/Jul/20

Thanking you

$${Thanking}\:{you} \\ $$

Commented by mr W last updated on 04/Jul/20

good sir!

$${good}\:{sir}! \\ $$

Commented by I want to learn more last updated on 04/Jul/20

Thanks sir

$$\mathrm{Thanks}\:\mathrm{sir} \\ $$

Answered by john santu last updated on 04/Jul/20

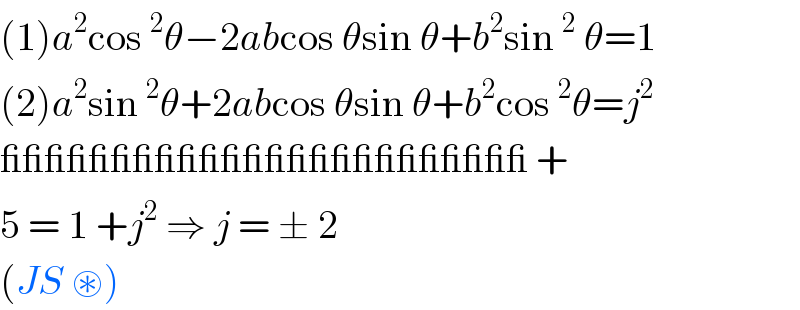
(1)a^2 cos^2 θ−2abcos θsin θ+b^2 sin^2 θ=1 (2)a^2 sin^2 θ+2abcos θsin θ+b^2 cos^2 θ=j^2 ________________________ + 5 = 1 +j^2 ⇒ j = ± 2 (JS ⊛)

$$\left(\mathrm{1}\right){a}^{\mathrm{2}} \mathrm{cos}\:^{\mathrm{2}} \theta−\mathrm{2}{ab}\mathrm{cos}\:\theta\mathrm{sin}\:\theta+{b}^{\mathrm{2}} \mathrm{sin}\:^{\mathrm{2}} \:\theta=\mathrm{1} \\ $$$$\left(\mathrm{2}\right){a}^{\mathrm{2}} \mathrm{sin}\:^{\mathrm{2}} \theta+\mathrm{2}{ab}\mathrm{cos}\:\theta\mathrm{sin}\:\theta+{b}^{\mathrm{2}} \mathrm{cos}\:^{\mathrm{2}} \theta={j}^{\mathrm{2}} \\ $$$$\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\:+ \\ $$$$\mathrm{5}\:=\:\mathrm{1}\:+{j}^{\mathrm{2}} \:\Rightarrow\:{j}\:=\:\pm\:\mathrm{2}\: \\ $$$$\left({JS}\:\circledast\right) \\ $$

Commented by I want to learn more last updated on 04/Jul/20

Thanks sir

$$\mathrm{Thanks}\:\mathrm{sir} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com