Question Number 101756 by bramlex last updated on 04/Jul/20

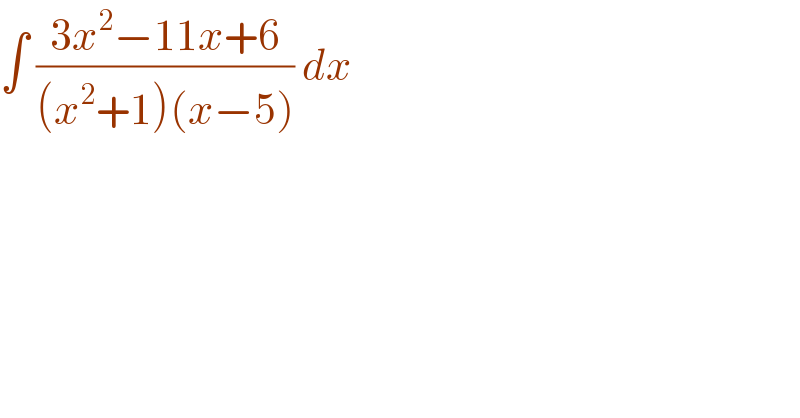
∫ ((3x^2 −11x+6)/((x^2 +1)(x−5))) dx

Answered by john santu last updated on 04/Jul/20

3x^2 −11x+6 = (x−5)(ax+b)+c(x^2 +1) x=0 ; 6 = −5b+c x=5 ; 26 = 26c ⇒c=1 ∧b = −1 x=−1; 20= (−6)(−a−1)+2 3 = a+1 ⇒a = 2 ∫ ((2x−1)/(x^2 +1)) dx + ∫ (1/(x−5)) dx = ∫ ((d(x^2 +1))/(x^2 +1)) − arctan (x) + ln∣x−5∣ + c = ln(x^2 +1)+ ln(x−5)−arctan (x) +c = ln((x^2 +1)(x−5))−arctan (x)+ c (JS ⊛ )

Answered by Dwaipayan Shikari last updated on 04/Jul/20

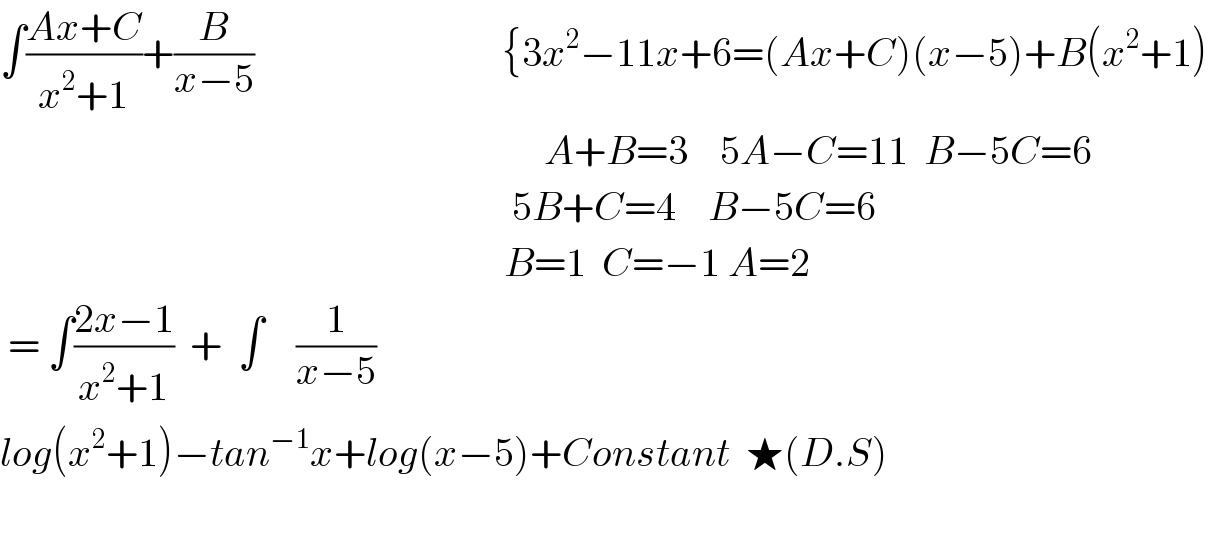
∫((Ax+C)/(x^2 +1))+(B/(x−5)) {3x^2 −11x+6=(Ax+C)(x−5)+B(x^2 +1) A+B=3 5A−C=11 B−5C=6 5B+C=4 B−5C=6 B=1 C=−1 A=2 = ∫((2x−1)/(x^2 +1)) + ∫ (1/(x−5)) log(x^2 +1)−tan^(−1) x+log(x−5)+Constant ★(D.S)