Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 101803 by dw last updated on 04/Jul/20

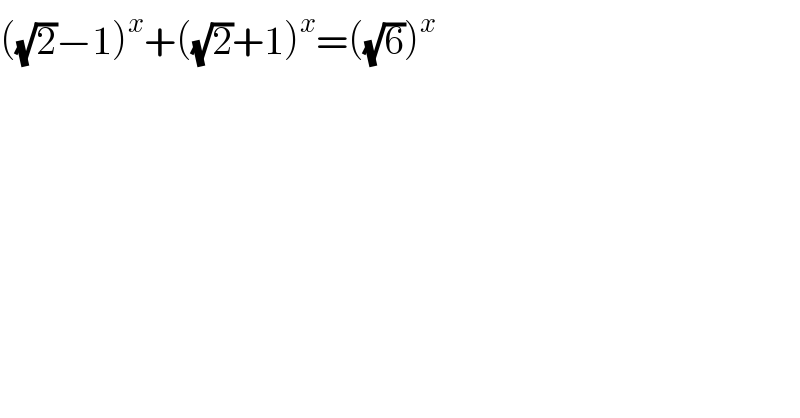
((√2)−1)^x +((√2)+1)^x =((√6))^x

$$\left(\sqrt{\mathrm{2}}−\mathrm{1}\right)^{{x}} +\left(\sqrt{\mathrm{2}}+\mathrm{1}\right)^{{x}} =\left(\sqrt{\mathrm{6}}\right)^{{x}} \\ $$

Commented by Dwaipayan Shikari last updated on 04/Jul/20

x=2

$${x}=\mathrm{2} \\ $$

Commented by dw last updated on 04/Jul/20

solution step by step please!

$${solution}\:{step}\:{by}\:{step}\:{please}! \\ $$

Answered by 1549442205 last updated on 05/Jul/20

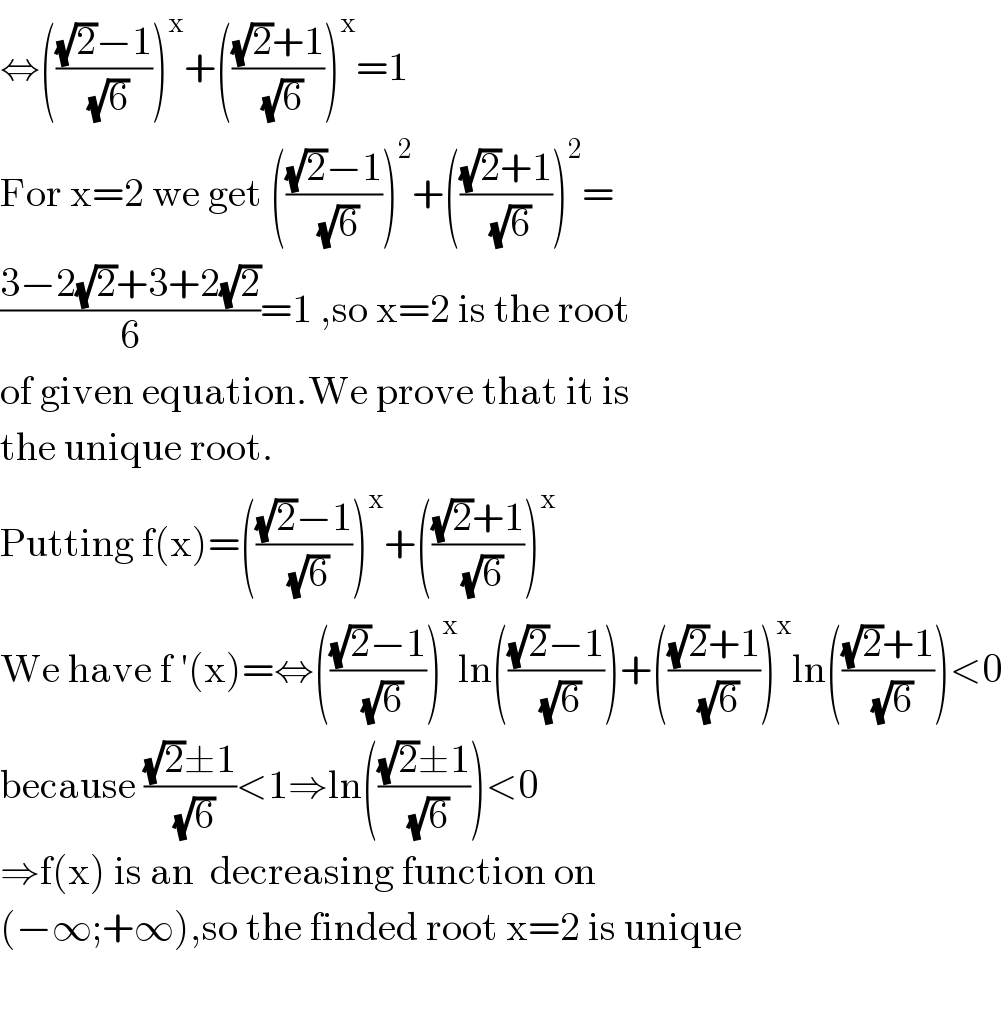
⇔((((√2)−1)/(√6)))^x +((((√2)+1)/(√6)))^x =1 For x=2 we get ((((√2)−1)/(√6)))^2 +((((√2)+1)/(√6)))^2 = ((3−2(√2)+3+2(√2))/6)=1 ,so x=2 is the root of given equation.We prove that it is the unique root. Putting f(x)=((((√2)−1)/(√6)))^x +((((√2)+1)/(√6)))^x We have f ′(x)=⇔((((√2)−1)/(√6)))^x ln((((√2)−1)/(√6)))+((((√2)+1)/(√6)))^x ln((((√2)+1)/(√6)))<0 because (((√2)±1)/(√6))<1⇒ln((((√2)±1)/(√6)))<0 ⇒f(x) is an decreasing function on (−∞;+∞),so the finded root x=2 is unique

$$\Leftrightarrow\left(\frac{\sqrt{\mathrm{2}}−\mathrm{1}}{\sqrt{\mathrm{6}}}\right)^{\mathrm{x}} +\left(\frac{\sqrt{\mathrm{2}}+\mathrm{1}}{\sqrt{\mathrm{6}}}\right)^{\mathrm{x}} =\mathrm{1} \\ $$$$\mathrm{For}\:\mathrm{x}=\mathrm{2}\:\mathrm{we}\:\mathrm{get}\:\left(\frac{\sqrt{\mathrm{2}}−\mathrm{1}}{\sqrt{\mathrm{6}}}\right)^{\mathrm{2}} +\left(\frac{\sqrt{\mathrm{2}}+\mathrm{1}}{\sqrt{\mathrm{6}}}\right)^{\mathrm{2}} = \\ $$$$\frac{\mathrm{3}−\mathrm{2}\sqrt{\mathrm{2}}+\mathrm{3}+\mathrm{2}\sqrt{\mathrm{2}}}{\mathrm{6}}=\mathrm{1}\:,\mathrm{so}\:\mathrm{x}=\mathrm{2}\:\mathrm{is}\:\mathrm{the}\:\mathrm{root}\: \\ $$$$\mathrm{of}\:\mathrm{given}\:\mathrm{equation}.\mathrm{We}\:\mathrm{prove}\:\mathrm{that}\:\mathrm{it}\:\mathrm{is}\: \\ $$$$\mathrm{the}\:\mathrm{unique}\:\mathrm{root}. \\ $$$$\mathrm{Putting}\:\mathrm{f}\left(\mathrm{x}\right)=\left(\frac{\sqrt{\mathrm{2}}−\mathrm{1}}{\sqrt{\mathrm{6}}}\right)^{\mathrm{x}} +\left(\frac{\sqrt{\mathrm{2}}+\mathrm{1}}{\sqrt{\mathrm{6}}}\right)^{\mathrm{x}} \\ $$$$\mathrm{We}\:\mathrm{have}\:\mathrm{f}\:'\left(\mathrm{x}\right)=\Leftrightarrow\left(\frac{\sqrt{\mathrm{2}}−\mathrm{1}}{\sqrt{\mathrm{6}}}\right)^{\mathrm{x}} \mathrm{ln}\left(\frac{\sqrt{\mathrm{2}}−\mathrm{1}}{\sqrt{\mathrm{6}}}\right)+\left(\frac{\sqrt{\mathrm{2}}+\mathrm{1}}{\sqrt{\mathrm{6}}}\right)^{\mathrm{x}} \mathrm{ln}\left(\frac{\sqrt{\mathrm{2}}+\mathrm{1}}{\sqrt{\mathrm{6}}}\right)<\mathrm{0} \\ $$$$\mathrm{because}\:\frac{\sqrt{\mathrm{2}}\pm\mathrm{1}}{\sqrt{\mathrm{6}}}<\mathrm{1}\Rightarrow\mathrm{ln}\left(\frac{\sqrt{\mathrm{2}}\pm\mathrm{1}}{\sqrt{\mathrm{6}}}\right)<\mathrm{0} \\ $$$$\Rightarrow\mathrm{f}\left(\mathrm{x}\right)\:\mathrm{is}\:\mathrm{an}\:\:\mathrm{decreasing}\:\mathrm{function}\:\mathrm{on} \\ $$$$\left(−\infty;+\infty\right),\mathrm{so}\:\mathrm{the}\:\mathrm{finded}\:\mathrm{root}\:\mathrm{x}=\mathrm{2}\:\mathrm{is}\:\mathrm{unique} \\ $$$$ \\ $$

Commented by dw last updated on 04/Jul/20

Thank you!

$${Thank}\:{you}! \\ $$

Commented by 1549442205 last updated on 05/Jul/20

You are welcome sir

$$\mathrm{You}\:\mathrm{are}\:\mathrm{welcome}\:\mathrm{sir} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com