
Question Number 101833 by bobhans last updated on 05/Jul/20
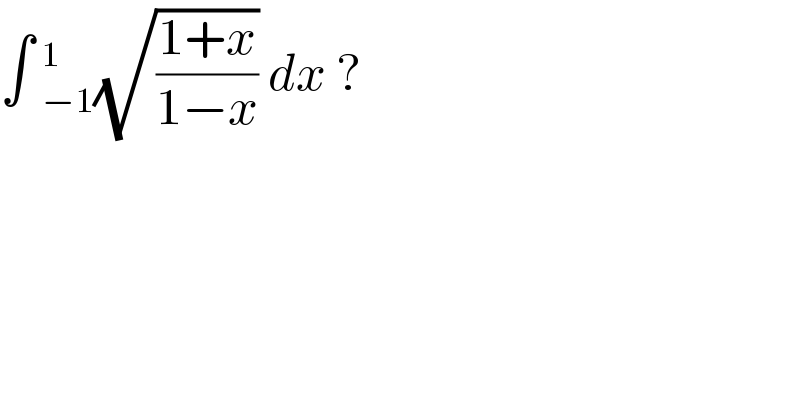
$$\int\:_{−\mathrm{1}} ^{\mathrm{1}} \sqrt{\frac{\mathrm{1}+{x}}{\mathrm{1}−{x}}}\:{dx}\:?\: \\ $$
Answered by Dwaipayan Shikari last updated on 05/Jul/20
![∫_(−1) ^1 ((1+x)/(√(1−x^2 )))dx=∫_(−1) ^1 (1/(√(1−x^2 )))+(x/(√(1−x^2 )))=[sin^(−1) x]_(−1) ^1 −(1/2)∫_(−1) ^1 ((−2x)/(√(1−x^2 )))dx =π−(1/2)[(√(1−x^2 ))]_(−1) ^1 =π+0=π](Q101862.png)
$$\int_{−\mathrm{1}} ^{\mathrm{1}} \frac{\mathrm{1}+{x}}{\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }}{dx}=\int_{−\mathrm{1}} ^{\mathrm{1}} \frac{\mathrm{1}}{\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }}+\frac{{x}}{\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }}=\left[{sin}^{−\mathrm{1}} {x}\right]_{−\mathrm{1}} ^{\mathrm{1}} −\frac{\mathrm{1}}{\mathrm{2}}\int_{−\mathrm{1}} ^{\mathrm{1}} \frac{−\mathrm{2}{x}}{\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }}{dx} \\ $$$$=\pi−\frac{\mathrm{1}}{\mathrm{2}}\left[\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }\right]_{−\mathrm{1}} ^{\mathrm{1}} =\pi+\mathrm{0}=\pi \\ $$$$ \\ $$
Answered by john santu last updated on 05/Jul/20
![set (√((1+x)/(1−x))) = s →dx = ((4s)/((s^2 +1)^2 )) ds I = ∫_0 ^∞ ((4s^2 )/((s^2 +1)^2 )) ds [ by parts ] { ((u = s)),((dv = ((4s ds)/((s^2 +1)^2 )))) :} I= −2.∣(s/(s^2 +1)) ∣_0 ^∞ −∫−((2 ds)/(s^2 +1)) I = 0+[ 2 arctan (s) ]_0 ^∞ I = 2((π/2)) = π (JS ⊛)](Q101834.png)
$${set}\:\sqrt{\frac{\mathrm{1}+{x}}{\mathrm{1}−{x}}}\:=\:{s}\:\rightarrow{dx}\:=\:\frac{\mathrm{4}{s}}{\left({s}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{2}} }\:{ds} \\ $$$${I}\:=\:\underset{\mathrm{0}} {\overset{\infty} {\int}}\:\frac{\mathrm{4}{s}^{\mathrm{2}} }{\left({s}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{2}} }\:{ds}\:\left[\:{by}\:{parts}\:\right] \\ $$$$\begin{cases}{{u}\:=\:{s}}\\{{dv}\:=\:\frac{\mathrm{4}{s}\:{ds}}{\left({s}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{2}} }}\end{cases} \\ $$$${I}=\:−\mathrm{2}.\mid\frac{{s}}{{s}^{\mathrm{2}} +\mathrm{1}}\:\mid_{\mathrm{0}} ^{\infty} −\int−\frac{\mathrm{2}\:{ds}}{{s}^{\mathrm{2}} +\mathrm{1}} \\ $$$${I}\:=\:\mathrm{0}+\left[\:\mathrm{2}\:\mathrm{arctan}\:\left({s}\right)\:\right]_{\mathrm{0}} ^{\infty} \: \\ $$$${I}\:=\:\mathrm{2}\left(\frac{\pi}{\mathrm{2}}\right)\:=\:\pi\:\:\left({JS}\:\circledast\right) \\ $$
Answered by mathmax by abdo last updated on 05/Jul/20
![A =∫_(−1) ^1 (√((1+x)/(1−x)))dx changement x =cost give A =−∫_0 ^π (√((1+cost)/(1−cost)))(−sint)dt =∫_0 ^π (√((2cos^2 ((t/2)))/(2sin^2 ((t/2)))))sint dt =∫_0 ^π ((cos((t/2)))/(sin((t/2)))) ×2sin((t/2))cos((t/2))dt =2∫_0 ^(π ) cos^2 ((t/2))dt =∫_0 ^π (1+cost)dt =π +∫_0 ^π cost dt =π +[sint]_0 ^π =π+0 ⇒A =π](Q101896.png)
$$\mathrm{A}\:=\int_{−\mathrm{1}} ^{\mathrm{1}} \sqrt{\frac{\mathrm{1}+\mathrm{x}}{\mathrm{1}−\mathrm{x}}}\mathrm{dx}\:\:\mathrm{changement}\:\mathrm{x}\:\:=\mathrm{cost}\:\mathrm{give}\: \\ $$$$\mathrm{A}\:=−\int_{\mathrm{0}} ^{\pi} \:\sqrt{\frac{\mathrm{1}+\mathrm{cost}}{\mathrm{1}−\mathrm{cost}}}\left(−\mathrm{sint}\right)\mathrm{dt}\:=\int_{\mathrm{0}} ^{\pi} \sqrt{\frac{\mathrm{2cos}^{\mathrm{2}} \left(\frac{\mathrm{t}}{\mathrm{2}}\right)}{\mathrm{2sin}^{\mathrm{2}} \left(\frac{\mathrm{t}}{\mathrm{2}}\right)}}\mathrm{sint}\:\mathrm{dt} \\ $$$$=\int_{\mathrm{0}} ^{\pi} \:\frac{\mathrm{cos}\left(\frac{\mathrm{t}}{\mathrm{2}}\right)}{\mathrm{sin}\left(\frac{\mathrm{t}}{\mathrm{2}}\right)}\:×\mathrm{2sin}\left(\frac{\mathrm{t}}{\mathrm{2}}\right)\mathrm{cos}\left(\frac{\mathrm{t}}{\mathrm{2}}\right)\mathrm{dt}\:=\mathrm{2}\int_{\mathrm{0}} ^{\pi\:} \mathrm{cos}^{\mathrm{2}} \left(\frac{\mathrm{t}}{\mathrm{2}}\right)\mathrm{dt} \\ $$$$=\int_{\mathrm{0}} ^{\pi} \left(\mathrm{1}+\mathrm{cost}\right)\mathrm{dt}\:=\pi\:+\int_{\mathrm{0}} ^{\pi} \:\mathrm{cost}\:\mathrm{dt}\:=\pi\:+\left[\mathrm{sint}\right]_{\mathrm{0}} ^{\pi} \:=\pi+\mathrm{0}\:\Rightarrow\mathrm{A}\:=\pi \\ $$
