Question Number 101835 by bobhans last updated on 05/Jul/20

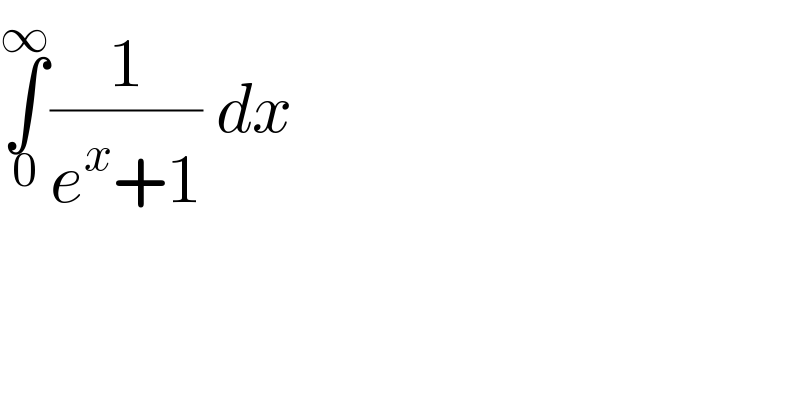
∫_0 ^∞ (1/(e^x +1)) dx

Answered by Dwaipayan Shikari last updated on 05/Jul/20

∫_0 ^∞ (e^x /(e^x (e^x +1)))dx=∫_0 ^∞ (dt/((t−1)t))=∫_2 ^∞ ((1/(t−1))−(1/t))dt=[log(((t−1)/t))]_2 ^∞ =log2 {suppose e^x +1=t

Answered by john santu last updated on 05/Jul/20

set e^x = tan ^2 p →dx = ((2sec ^2 p dp)/(tan p)) I= 2∫_(π/4) ^(π/2) ((sec ^2 p dp)/(tan p(tan ^2 p+1))) I = 2∫_(π/4) ^(π/2) cot p dp = 2[ ln ∣sin p∣]_(π/4) ^(π/2) = 2ln(1)−2ln(((√2)/2)) = ln(2) (JS ⊛)

Answered by mathmax by abdo last updated on 05/Jul/20

I =∫_0 ^∞ (dx/(e^x +1)) we do the changement e^x =t ⇒I =∫_1 ^(+∞) (dt/(t(t+1))) =∫_1 ^∞ ((1/t)−(1/(t+1)))dt =[ln∣(t/(t+1))∣]_1 ^∞ =−ln((1/2)) =ln(2)