Question and Answers Forum

All Questions      Topic List

Differential Equation Questions

Previous in All Question      Next in All Question      

Previous in Differential Equation      Next in Differential Equation      

Question Number 101846 by bemath last updated on 05/Jul/20

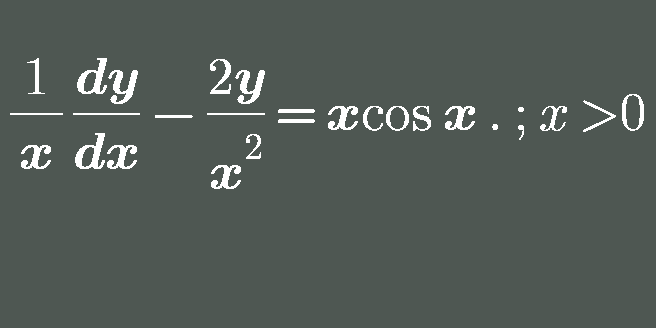
Answered by bramlex last updated on 05/Jul/20

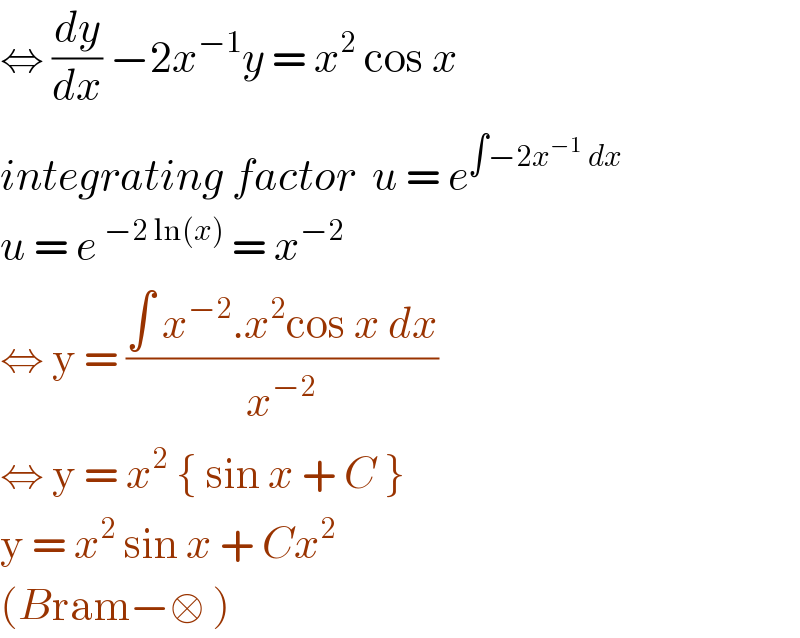
⇔ (dy/dx) −2x^(−1) y = x^2 cos x integrating factor u = e^(∫−2x^(−1) dx) u = e^(−2 ln(x)) = x^(−2) ⇔ y = ((∫ x^(−2) .x^2 cos x dx)/x^(−2) ) ⇔ y = x^2 { sin x + C } y = x^2 sin x + Cx^2 (Bram−□ )

$$\Leftrightarrow\:\frac{{dy}}{{dx}}\:−\mathrm{2}{x}^{−\mathrm{1}} {y}\:=\:{x}^{\mathrm{2}} \:\mathrm{cos}\:{x} \\ $$$${integrating}\:{factor}\:\:{u}\:=\:{e}^{\int−\mathrm{2}{x}^{−\mathrm{1}} \:{dx}} \\ $$$${u}\:=\:{e}\:^{−\mathrm{2}\:\mathrm{ln}\left({x}\right)} \:=\:{x}^{−\mathrm{2}} \\ $$$$\Leftrightarrow\:\mathrm{y}\:=\:\frac{\int\:{x}^{−\mathrm{2}} .{x}^{\mathrm{2}} \mathrm{cos}\:{x}\:{dx}}{{x}^{−\mathrm{2}} } \\ $$$$\Leftrightarrow\:\mathrm{y}\:=\:{x}^{\mathrm{2}} \:\left\{\:\mathrm{sin}\:{x}\:+\:{C}\:\right\}\: \\ $$$$\mathrm{y}\:=\:{x}^{\mathrm{2}} \:\mathrm{sin}\:{x}\:+\:{Cx}^{\mathrm{2}} \: \\ $$$$\left({B}\mathrm{ram}−\square\:\right)\: \\ $$

Answered by mathmax by abdo last updated on 05/Jul/20

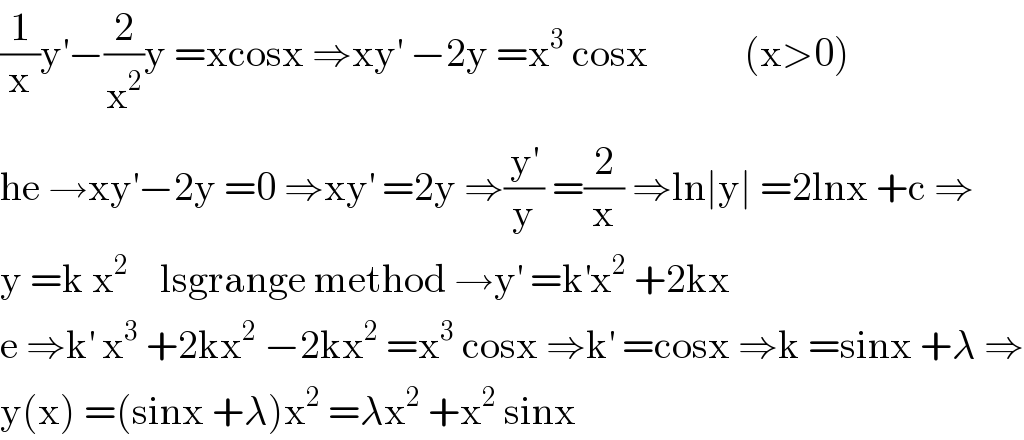
(1/x)y^′ −(2/x^2 )y =xcosx ⇒xy^′ −2y =x^3 cosx (x>0) he →xy^′ −2y =0 ⇒xy^′ =2y ⇒(y^′ /y) =(2/x) ⇒ln∣y∣ =2lnx +c ⇒ y =k x^2 lsgrange method →y^′ =k^′ x^2 +2kx e ⇒k^′ x^3 +2kx^2 −2kx^2 =x^3 cosx ⇒k^′ =cosx ⇒k =sinx +λ ⇒ y(x) =(sinx +λ)x^2 =λx^2 +x^2 sinx

$$\frac{\mathrm{1}}{\mathrm{x}}\mathrm{y}^{'} −\frac{\mathrm{2}}{\mathrm{x}^{\mathrm{2}} }\mathrm{y}\:=\mathrm{xcosx}\:\Rightarrow\mathrm{xy}^{'} \:−\mathrm{2y}\:=\mathrm{x}^{\mathrm{3}} \:\mathrm{cosx}\:\:\:\:\:\:\:\:\:\:\:\:\left(\mathrm{x}>\mathrm{0}\right) \\ $$$$\mathrm{he}\:\rightarrow\mathrm{xy}^{'} −\mathrm{2y}\:=\mathrm{0}\:\Rightarrow\mathrm{xy}^{'} \:=\mathrm{2y}\:\Rightarrow\frac{\mathrm{y}^{'} }{\mathrm{y}}\:=\frac{\mathrm{2}}{\mathrm{x}}\:\Rightarrow\mathrm{ln}\mid\mathrm{y}\mid\:=\mathrm{2lnx}\:+\mathrm{c}\:\Rightarrow \\ $$$$\mathrm{y}\:=\mathrm{k}\:\mathrm{x}^{\mathrm{2}} \:\:\:\:\mathrm{lsgrange}\:\mathrm{method}\:\rightarrow\mathrm{y}^{'} \:=\mathrm{k}^{'} \mathrm{x}^{\mathrm{2}} \:+\mathrm{2kx} \\ $$$$\mathrm{e}\:\Rightarrow\mathrm{k}^{'} \:\mathrm{x}^{\mathrm{3}} \:+\mathrm{2kx}^{\mathrm{2}} \:−\mathrm{2kx}^{\mathrm{2}} \:=\mathrm{x}^{\mathrm{3}} \:\mathrm{cosx}\:\Rightarrow\mathrm{k}^{'} \:=\mathrm{cosx}\:\Rightarrow\mathrm{k}\:=\mathrm{sinx}\:+\lambda\:\Rightarrow \\ $$$$\mathrm{y}\left(\mathrm{x}\right)\:=\left(\mathrm{sinx}\:+\lambda\right)\mathrm{x}^{\mathrm{2}} \:=\lambda\mathrm{x}^{\mathrm{2}} \:+\mathrm{x}^{\mathrm{2}} \:\mathrm{sinx} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com