Question and Answers Forum

All Questions      Topic List

Differential Equation Questions

Previous in All Question      Next in All Question      

Previous in Differential Equation      Next in Differential Equation      

Question Number 101848 by bramlex last updated on 05/Jul/20

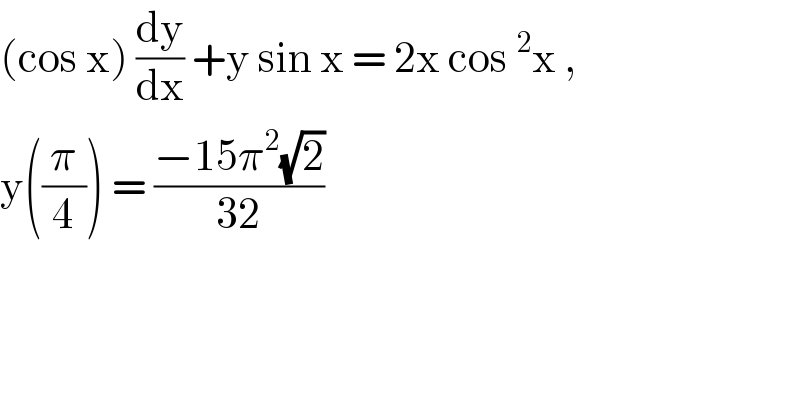
(cos x) (dy/dx) +y sin x = 2x cos^2 x , y((π/4)) = ((−15π^2 (√2))/(32))

$$\left(\mathrm{cos}\:\mathrm{x}\right)\:\frac{\mathrm{dy}}{\mathrm{dx}}\:+\mathrm{y}\:\mathrm{sin}\:\mathrm{x}\:=\:\mathrm{2x}\:\mathrm{cos}\:^{\mathrm{2}} \mathrm{x}\:, \\ $$$$\mathrm{y}\left(\frac{\pi}{\mathrm{4}}\right)\:=\:\frac{−\mathrm{15}\pi^{\mathrm{2}} \sqrt{\mathrm{2}}}{\mathrm{32}} \\ $$

Answered by john santu last updated on 05/Jul/20

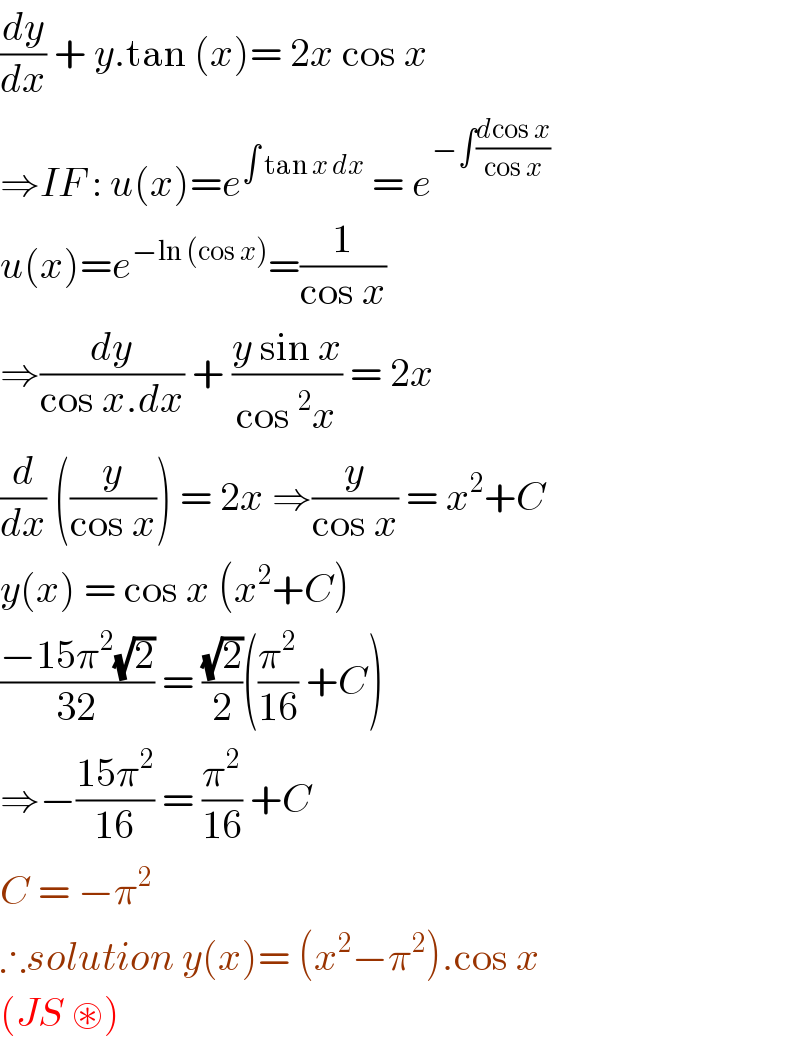
(dy/dx) + y.tan (x)= 2x cos x ⇒IF : u(x)=e^(∫ tan x dx) = e^(−∫((dcos x)/(cos x))) u(x)=e^(−ln (cos x)) =(1/(cos x)) ⇒(dy/(cos x.dx)) + ((y sin x)/(cos^2 x)) = 2x (d/dx) ((y/(cos x))) = 2x ⇒(y/(cos x)) = x^2 +C y(x) = cos x (x^2 +C) ((−15π^2 (√2))/(32)) = ((√2)/2)((π^2 /(16)) +C) ⇒−((15π^2 )/(16)) = (π^2 /(16)) +C C = −π^2 ∴solution y(x)= (x^2 −π^2 ).cos x (JS ⊛)

$$\frac{{dy}}{{dx}}\:+\:{y}.\mathrm{tan}\:\left({x}\right)=\:\mathrm{2}{x}\:\mathrm{cos}\:{x} \\ $$$$\Rightarrow{IF}\::\:{u}\left({x}\right)={e}^{\int\:\mathrm{tan}\:{x}\:{dx}} \:=\:{e}^{−\int\frac{{d}\mathrm{cos}\:{x}}{\mathrm{cos}\:{x}}} \\ $$$${u}\left({x}\right)={e}^{−\mathrm{ln}\:\left(\mathrm{cos}\:{x}\right)} =\frac{\mathrm{1}}{\mathrm{cos}\:{x}} \\ $$$$\Rightarrow\frac{{dy}}{\mathrm{cos}\:{x}.{dx}}\:+\:\frac{{y}\:\mathrm{sin}\:{x}}{\mathrm{cos}\:^{\mathrm{2}} {x}}\:=\:\mathrm{2}{x} \\ $$$$\frac{{d}}{{dx}}\:\left(\frac{{y}}{\mathrm{cos}\:{x}}\right)\:=\:\mathrm{2}{x}\:\Rightarrow\frac{{y}}{\mathrm{cos}\:{x}}\:=\:{x}^{\mathrm{2}} +{C} \\ $$$${y}\left({x}\right)\:=\:\mathrm{cos}\:{x}\:\left({x}^{\mathrm{2}} +{C}\right) \\ $$$$\frac{−\mathrm{15}\pi^{\mathrm{2}} \sqrt{\mathrm{2}}}{\mathrm{32}}\:=\:\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}\left(\frac{\pi^{\mathrm{2}} }{\mathrm{16}}\:+{C}\right) \\ $$$$\Rightarrow−\frac{\mathrm{15}\pi^{\mathrm{2}} }{\mathrm{16}}\:=\:\frac{\pi^{\mathrm{2}} }{\mathrm{16}}\:+{C} \\ $$$${C}\:=\:−\pi^{\mathrm{2}} \\ $$$$\therefore{solution}\:{y}\left({x}\right)=\:\left({x}^{\mathrm{2}} −\pi^{\mathrm{2}} \right).\mathrm{cos}\:{x}\: \\ $$$$\left({JS}\:\circledast\right) \\ $$

Commented by bramlex last updated on 05/Jul/20

macho...������

Answered by mathmax by abdo last updated on 05/Jul/20

cosx y^′ +sinx y =2xcos^2 x with y((π/4)) =−((15π(√2))/(32)) he→cosx y^′ +sinx y =0 ⇒cosx y^′ =−sinx y ⇒(y^′ /y) =−((sinx)/(cosx)) ⇒ ln∣y∣ =ln(cosx)+c ⇒y =k cosx lagrange method →y^′ =k^′ cosx −ksinx e⇒k^′ cos^2 x−kcosx sinx +ksinx cosx =2xcos^2 x ⇒k^′ =2x ⇒k(x) =x^2 +λ ⇒ y(x) =(x^2 +λ)cosx y((π/4)) =−((15π(√2))/(32)) ⇒((π^2 /8) +λ)×((√2)/2) =−((15π(√2))/(32)) ⇒λ +(π^2 /8) =−((15π)/(16)) ⇒ λ =−(π^2 /8)−((15π)/(16)) =−((17π)/(16)) ⇒y(x) =(x^2 −((17π)/(16)))cosx

$$\mathrm{cosx}\:\mathrm{y}^{'} \:+\mathrm{sinx}\:\mathrm{y}\:=\mathrm{2xcos}^{\mathrm{2}} \mathrm{x}\:\:\mathrm{with}\:\mathrm{y}\left(\frac{\pi}{\mathrm{4}}\right)\:=−\frac{\mathrm{15}\pi\sqrt{\mathrm{2}}}{\mathrm{32}} \\ $$$$\mathrm{he}\rightarrow\mathrm{cosx}\:\mathrm{y}^{'} \:+\mathrm{sinx}\:\mathrm{y}\:=\mathrm{0}\:\Rightarrow\mathrm{cosx}\:\mathrm{y}^{'} \:=−\mathrm{sinx}\:\mathrm{y}\:\Rightarrow\frac{\mathrm{y}^{'} }{\mathrm{y}}\:=−\frac{\mathrm{sinx}}{\mathrm{cosx}}\:\Rightarrow \\ $$$$\mathrm{ln}\mid\mathrm{y}\mid\:=\mathrm{ln}\left(\mathrm{cosx}\right)+\mathrm{c}\:\Rightarrow\mathrm{y}\:=\mathrm{k}\:\mathrm{cosx} \\ $$$$\mathrm{lagrange}\:\mathrm{method}\:\rightarrow\mathrm{y}^{'} \:=\mathrm{k}^{'} \:\mathrm{cosx}\:−\mathrm{ksinx} \\ $$$$\mathrm{e}\Rightarrow\mathrm{k}^{'} \:\mathrm{cos}^{\mathrm{2}} \mathrm{x}−\mathrm{kcosx}\:\mathrm{sinx}\:+\mathrm{ksinx}\:\mathrm{cosx}\:=\mathrm{2xcos}^{\mathrm{2}} \mathrm{x}\:\Rightarrow\mathrm{k}^{'} \:=\mathrm{2x}\:\Rightarrow\mathrm{k}\left(\mathrm{x}\right)\:=\mathrm{x}^{\mathrm{2}} \:+\lambda\:\Rightarrow \\ $$$$\mathrm{y}\left(\mathrm{x}\right)\:=\left(\mathrm{x}^{\mathrm{2}} \:+\lambda\right)\mathrm{cosx}\: \\ $$$$\mathrm{y}\left(\frac{\pi}{\mathrm{4}}\right)\:=−\frac{\mathrm{15}\pi\sqrt{\mathrm{2}}}{\mathrm{32}}\:\Rightarrow\left(\frac{\pi^{\mathrm{2}} }{\mathrm{8}}\:+\lambda\right)×\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}\:=−\frac{\mathrm{15}\pi\sqrt{\mathrm{2}}}{\mathrm{32}}\:\Rightarrow\lambda\:+\frac{\pi^{\mathrm{2}} }{\mathrm{8}}\:=−\frac{\mathrm{15}\pi}{\mathrm{16}}\:\Rightarrow \\ $$$$\lambda\:=−\frac{\pi^{\mathrm{2}} }{\mathrm{8}}−\frac{\mathrm{15}\pi}{\mathrm{16}}\:=−\frac{\mathrm{17}\pi}{\mathrm{16}}\:\Rightarrow\mathrm{y}\left(\mathrm{x}\right)\:=\left(\mathrm{x}^{\mathrm{2}} −\frac{\mathrm{17}\pi}{\mathrm{16}}\right)\mathrm{cosx} \\ $$

Commented by john santu last updated on 05/Jul/20

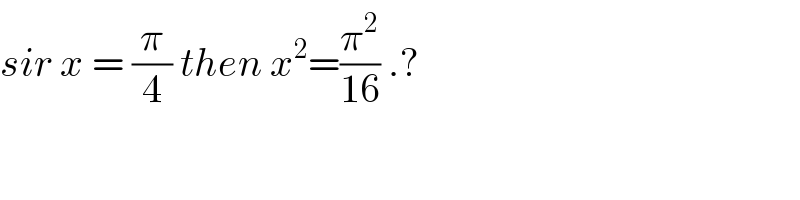
sir x = (π/4) then x^2 =(π^2 /(16)) .?

$${sir}\:{x}\:=\:\frac{\pi}{\mathrm{4}}\:{then}\:{x}^{\mathrm{2}} =\frac{\pi^{\mathrm{2}} }{\mathrm{16}}\:.? \\ $$$$ \\ $$

Commented by mathmax by abdo last updated on 05/Jul/20

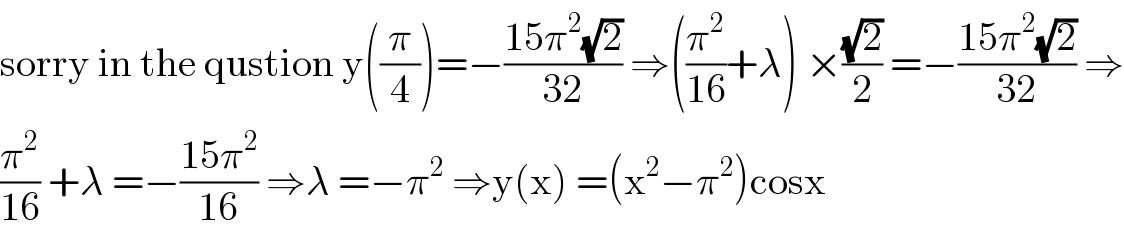
sorry in the qustion y((π/4))=−((15π^2 (√2))/(32)) ⇒((π^2 /(16))+λ) ×((√2)/2) =−((15π^2 (√2))/(32)) ⇒ (π^2 /(16)) +λ =−((15π^2 )/(16)) ⇒λ =−π^2 ⇒y(x) =(x^2 −π^2 )cosx

$$\mathrm{sorry}\:\mathrm{in}\:\mathrm{the}\:\mathrm{qustion}\:\mathrm{y}\left(\frac{\pi}{\mathrm{4}}\right)=−\frac{\mathrm{15}\pi^{\mathrm{2}} \sqrt{\mathrm{2}}}{\mathrm{32}}\:\Rightarrow\left(\frac{\pi^{\mathrm{2}} }{\mathrm{16}}+\lambda\right)\:×\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}\:=−\frac{\mathrm{15}\pi^{\mathrm{2}} \sqrt{\mathrm{2}}}{\mathrm{32}}\:\Rightarrow \\ $$$$\frac{\pi^{\mathrm{2}} }{\mathrm{16}}\:+\lambda\:=−\frac{\mathrm{15}\pi^{\mathrm{2}} }{\mathrm{16}}\:\Rightarrow\lambda\:=−\pi^{\mathrm{2}} \:\Rightarrow\mathrm{y}\left(\mathrm{x}\right)\:=\left(\mathrm{x}^{\mathrm{2}} −\pi^{\mathrm{2}} \right)\mathrm{cosx} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com