
Question Number 101882 by bachamohamed last updated on 05/Jul/20

$$\:\:\:\int\frac{\mathrm{1}}{\sqrt{\boldsymbol{{x}}}+\sqrt{\boldsymbol{{x}}+\mathrm{1}}+\sqrt{\boldsymbol{{x}}+\mathrm{2}}}\boldsymbol{{dx}} \\ $$
Commented by M±th+et+s last updated on 05/Jul/20

$${and}\:{till}\:{now}\:{i}\:{am}\:{trying}\:{with}\:{this} \\ $$$$ \\ $$$$\frac{\mathrm{1}}{\sqrt{{x}}+\sqrt{{x}+\mathrm{1}}+\sqrt{{x}+\mathrm{2}}}=\frac{\mathrm{1}}{\mathrm{4}{x}^{\mathrm{3}} −{x}^{\mathrm{2}} +\mathrm{6}{x}−\mathrm{4}}\left(\left({x}+\mathrm{1}\right)\sqrt{{x}+\mathrm{1}}+\left({x}−\mathrm{1}\right)\sqrt{{x}+\mathrm{2}}−\mathrm{2}\sqrt{{x}}\sqrt{{x}+\mathrm{1}}\sqrt{{x}+\mathrm{2}}+\frac{\mathrm{1}−{x}^{\mathrm{2}} }{\mathrm{2}\sqrt{{x}}}\right)+\frac{\mathrm{1}}{\mathrm{2}\sqrt{{x}}} \\ $$$${mybe}\:{i}\:{will}\:{find}\:{an}\:{elementary}\:{solution} \\ $$$$ \\ $$
Answered by Dwaipayan Shikari last updated on 05/Jul/20
![∫(1/((√(4x+2))+(√(x+2))))dx {(√(x+1))+(√x)=(√(4x+2 )) x≠0 and x∈N ∫(((√(4x+2))−(√(x+2)))/(3x))dx ∫((√(4x+2))/(3x))−∫((√(x+2))/(3x)) (1/6)∫((t^2 dt)/((t^2 −2)/4))dt−(2/3)∫(p^2 /(p^2 −2))dp {suppose (√(4x+2))=t and (√(x+2))=p (2/3)[∫(t^2 /(t^2 −2)) dt −∫(p^2 /(p^2 −2))dp]=(2/3)((t−(1/(2(√2)))log(((t−(√2))/(t+(√2)))))−(2/3)((p−(1/(2(√2)))log(((p−(√2))/(p+(√2)))))+C =(2/3)((√(4x+2))−(1/(2(√2)))log((((√(4x+2))−(√2))/((√(4x+2))+(√2))))−(√(x+2))+(1/(2(√2)))log((((√(x+2))−(√2))/((√(x+2))+(√2)))))+Constant But this is not a rigorous solution. This only happens in this condition . This is proved by Ramanujan ((√x)+(√(x+1))=(√(4x+2)) x≠0 x∈N)](Q101898.png)
$$\int\frac{\mathrm{1}}{\sqrt{\mathrm{4}{x}+\mathrm{2}}+\sqrt{{x}+\mathrm{2}}}{dx}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\left\{\sqrt{{x}+\mathrm{1}}+\sqrt{{x}}=\sqrt{\mathrm{4}{x}+\mathrm{2}\:\:}\:{x}\neq\mathrm{0}\:\:\:{and}\:{x}\in\mathbb{N}\right. \\ $$$$\int\frac{\sqrt{\mathrm{4}{x}+\mathrm{2}}−\sqrt{{x}+\mathrm{2}}}{\mathrm{3}{x}}{dx} \\ $$$$\int\frac{\sqrt{\mathrm{4}{x}+\mathrm{2}}}{\mathrm{3}{x}}−\int\frac{\sqrt{{x}+\mathrm{2}}}{\mathrm{3}{x}} \\ $$$$\frac{\mathrm{1}}{\mathrm{6}}\int\frac{{t}^{\mathrm{2}} {dt}}{\frac{{t}^{\mathrm{2}} −\mathrm{2}}{\mathrm{4}}}{dt}−\frac{\mathrm{2}}{\mathrm{3}}\int\frac{{p}^{\mathrm{2}} }{{p}^{\mathrm{2}} −\mathrm{2}}{dp}\:\:\:\:\left\{{suppose}\:\sqrt{\mathrm{4}{x}+\mathrm{2}}={t}\:\:{and}\:\sqrt{{x}+\mathrm{2}}={p}\right. \\ $$$$\frac{\mathrm{2}}{\mathrm{3}}\left[\int\frac{{t}^{\mathrm{2}} }{{t}^{\mathrm{2}} −\mathrm{2}}\:{dt}\:−\int\frac{{p}^{\mathrm{2}} }{{p}^{\mathrm{2}} −\mathrm{2}}{dp}\right]=\frac{\mathrm{2}}{\mathrm{3}}\left(\left({t}−\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{2}}}{log}\left(\frac{{t}−\sqrt{\mathrm{2}}}{{t}+\sqrt{\mathrm{2}}}\right)\right)−\frac{\mathrm{2}}{\mathrm{3}}\left(\left({p}−\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{2}}}{log}\left(\frac{{p}−\sqrt{\mathrm{2}}}{{p}+\sqrt{\mathrm{2}}}\right)\right)+{C}\right.\right. \\ $$$$ \\ $$$$=\frac{\mathrm{2}}{\mathrm{3}}\left(\sqrt{\mathrm{4}{x}+\mathrm{2}}−\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{2}}}{log}\left(\frac{\sqrt{\mathrm{4}{x}+\mathrm{2}}−\sqrt{\mathrm{2}}}{\sqrt{\mathrm{4}{x}+\mathrm{2}}+\sqrt{\mathrm{2}}}\right)−\sqrt{{x}+\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{2}}}{log}\left(\frac{\sqrt{{x}+\mathrm{2}}−\sqrt{\mathrm{2}}}{\sqrt{{x}+\mathrm{2}}+\sqrt{\mathrm{2}}}\right)\right)+{Constant} \\ $$$$ \\ $$$${But}\:{this}\:{is}\:{not}\:{a}\:{rigorous}\:{solution}. \\ $$$${This}\:{only}\:{happens}\:{in}\:{this}\:{condition}\:. \\ $$$$ \\ $$$${This}\:{is}\:{proved}\:{by}\:{Ramanujan}\:\:\left(\sqrt{{x}}+\sqrt{{x}+\mathrm{1}}=\sqrt{\mathrm{4}{x}+\mathrm{2}}\:\:\:{x}\neq\mathrm{0}\:\:{x}\in\mathbb{N}\right) \\ $$
Commented by prakash jain last updated on 05/Jul/20
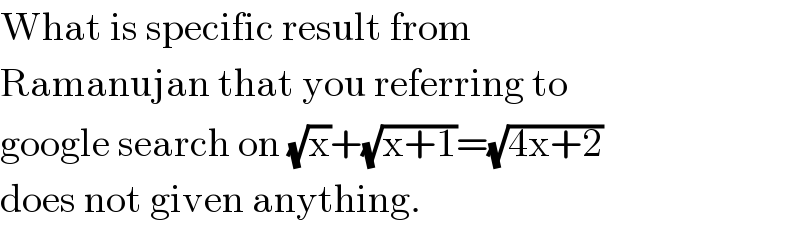
$$\mathrm{What}\:\mathrm{is}\:\mathrm{specific}\:\mathrm{result}\:\mathrm{from} \\ $$$$\mathrm{Ramanujan}\:\mathrm{that}\:\mathrm{you}\:\mathrm{referring}\:\mathrm{to} \\ $$$$\mathrm{google}\:\mathrm{search}\:\mathrm{on}\:\sqrt{\mathrm{x}}+\sqrt{\mathrm{x}+\mathrm{1}}=\sqrt{\mathrm{4x}+\mathrm{2}} \\ $$$$\mathrm{does}\:\mathrm{not}\:\mathrm{given}\:\mathrm{anything}. \\ $$
Commented by Dwaipayan Shikari last updated on 05/Jul/20
https://youtu.be/jGiK3NSsHro (watch this video of Michael Penn)
Commented by Dwaipayan Shikari last updated on 05/Jul/20

$${sorry}\:{it}\:{will}\:{be}\:{x}\in\mathbb{N} \\ $$
Commented by prakash jain last updated on 05/Jul/20
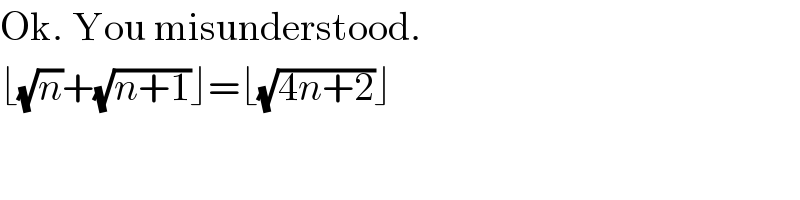
$$\mathrm{Ok}.\:\mathrm{You}\:\mathrm{misunderstood}. \\ $$$$\lfloor\sqrt{{n}}+\sqrt{{n}+\mathrm{1}}\rfloor=\lfloor\sqrt{\mathrm{4}{n}+\mathrm{2}}\rfloor \\ $$
Commented by Dwaipayan Shikari last updated on 05/Jul/20
$${Yes}\:{sir}.\:{I}\:{am}\:{a}\:{high}\:{school}\:{student}.\:{Kindly}\:{forgive}\:{my}\:{misunderstanding} \\ $$
