Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 101921 by Farruxjano last updated on 05/Jul/20

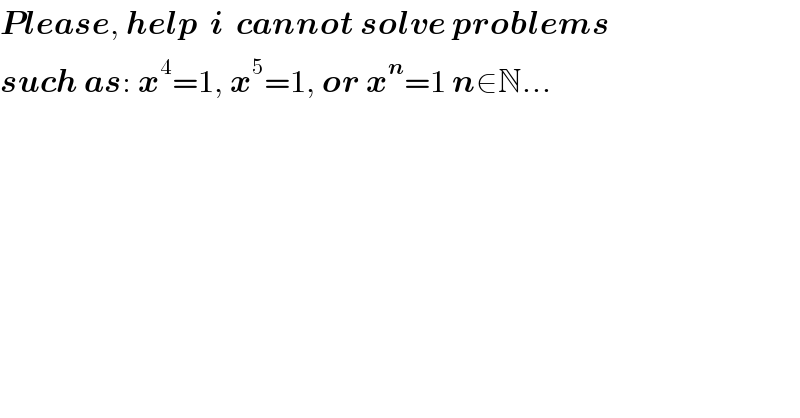
Please, help i cannot solve problems such as: x^4 =1, x^5 =1, or x^n =1 n∈N...

$$\boldsymbol{{Please}},\:\boldsymbol{{help}}\:\:\boldsymbol{{i}}\:\:\boldsymbol{{cannot}}\:\boldsymbol{{solve}}\:\boldsymbol{{problems}} \\ $$$$\boldsymbol{{such}}\:\boldsymbol{{as}}:\:\boldsymbol{{x}}^{\mathrm{4}} =\mathrm{1},\:\boldsymbol{{x}}^{\mathrm{5}} =\mathrm{1},\:\boldsymbol{{or}}\:\boldsymbol{{x}}^{\boldsymbol{{n}}} =\mathrm{1}\:\boldsymbol{{n}}\in\mathbb{N}... \\ $$

Commented by prakash jain last updated on 05/Jul/20

Search internet for roots of unity. You will find lot of information. to start with i=(√(−1)) e^(iθ) =cos θ+isin θ 1=cos 2πk+isin 2πk 1^(1/n) =e^((2πj)/n) (j=0,....n−1) as you can see (e^((2πj)/n) )^n =e^(2jπ) =1

$$\mathrm{Search}\:\mathrm{internet}\:\mathrm{for}\:\mathrm{roots}\:\mathrm{of}\:\mathrm{unity}. \\ $$$$\mathrm{You}\:\mathrm{will}\:\mathrm{find}\:\mathrm{lot}\:\mathrm{of}\:\mathrm{information}. \\ $$$$\mathrm{to}\:\mathrm{start}\:\mathrm{with}\:{i}=\sqrt{−\mathrm{1}} \\ $$$${e}^{{i}\theta} =\mathrm{cos}\:\theta+{i}\mathrm{sin}\:\theta \\ $$$$\mathrm{1}=\mathrm{cos}\:\mathrm{2}\pi{k}+{i}\mathrm{sin}\:\mathrm{2}\pi{k} \\ $$$$\mathrm{1}^{\mathrm{1}/{n}} ={e}^{\frac{\mathrm{2}\pi{j}}{{n}}} \:\:\left({j}=\mathrm{0},....{n}−\mathrm{1}\right) \\ $$$$\mathrm{as}\:\mathrm{you}\:\mathrm{can}\:\mathrm{see}\:\left({e}^{\frac{\mathrm{2}\pi{j}}{{n}}} \right)^{{n}} ={e}^{\mathrm{2}{j}\pi} =\mathrm{1} \\ $$

Answered by 1549442205 last updated on 06/Jul/20

Applying the Mauvra′s formular (cosϕ+isinϕ)^n =cosnϕ+isinnϕ Since 1=cos2kπ+isin2kπ ,so i)For the eqs.x^4 =1 we get x=1^(1/4) ⇔x=(cos2kπ+isin2kπ)^(1/4) =cos((2kπ)/4)+isin((2kπ)/4)(k=0,1,2,3) we get four different roots ii)For the eqs.x^5 =1⇔x=1^(1/5) .We get x=(cos2kπ+isin2kπ)^(1/5) ⇔x=cos((2kπ)/5)+isin((2kπ)/5)(k∈{0,1,2,3,4}) weget five different roots iii)For eqs.x^n =1⇔x=1^(1/n) .We get x=(cos2kπ+isin2kπ)^(1/n) =cos((2kπ)/n)+isin((2kπ)/n)(n∈{0,1,2,...n−1}) weget n different roots for k=n,n+1,n+2,... we get the repeated roots

$$\mathrm{Applying}\:\mathrm{the}\:\mathrm{Mauvra}'\mathrm{s}\:\mathrm{formular}\: \\ $$$$\left(\mathrm{cos}\varphi+\mathrm{isin}\varphi\right)^{\mathrm{n}} =\mathrm{cosn}\varphi+\mathrm{isinn}\varphi\: \\ $$$$\mathrm{Since}\:\mathrm{1}=\mathrm{cos2k}\pi+\mathrm{isin2k}\pi\:,\mathrm{so} \\ $$$$\left.\mathrm{i}\right)\mathrm{For}\:\mathrm{the}\:\mathrm{eqs}.\mathrm{x}^{\mathrm{4}} =\mathrm{1}\:\mathrm{we}\:\mathrm{get}\:\mathrm{x}=\mathrm{1}^{\frac{\mathrm{1}}{\mathrm{4}}} \\ $$$$\Leftrightarrow\mathrm{x}=\left(\mathrm{cos2k}\pi+\mathrm{isin2k}\pi\right)^{\frac{\mathrm{1}}{\mathrm{4}}} =\mathrm{cos}\frac{\mathrm{2k}\pi}{\mathrm{4}}+\mathrm{isin}\frac{\mathrm{2k}\pi}{\mathrm{4}}\left(\mathrm{k}=\mathrm{0},\mathrm{1},\mathrm{2},\mathrm{3}\right) \\ $$$$\mathrm{we}\:\mathrm{get}\:\mathrm{four}\:\mathrm{different}\:\mathrm{roots}\: \\ $$$$\left.\mathrm{ii}\right)\mathrm{For}\:\mathrm{the}\:\mathrm{eqs}.\mathrm{x}^{\mathrm{5}} =\mathrm{1}\Leftrightarrow\mathrm{x}=\mathrm{1}^{\frac{\mathrm{1}}{\mathrm{5}}} .\mathrm{We}\:\mathrm{get} \\ $$$$\mathrm{x}=\left(\mathrm{cos2k}\pi+\mathrm{isin2k}\pi\right)^{\frac{\mathrm{1}}{\mathrm{5}}} \Leftrightarrow\mathrm{x}=\mathrm{cos}\frac{\mathrm{2k}\pi}{\mathrm{5}}+\mathrm{isin}\frac{\mathrm{2k}\pi}{\mathrm{5}}\left(\mathrm{k}\in\left\{\mathrm{0},\mathrm{1},\mathrm{2},\mathrm{3},\mathrm{4}\right\}\right) \\ $$$$\mathrm{weget}\:\mathrm{five}\:\mathrm{different}\:\:\mathrm{roots} \\ $$$$\left.\mathrm{iii}\right)\mathrm{For}\:\mathrm{eqs}.\mathrm{x}^{\mathrm{n}} =\mathrm{1}\Leftrightarrow\mathrm{x}=\mathrm{1}^{\frac{\mathrm{1}}{\mathrm{n}}} .\mathrm{We}\:\mathrm{get} \\ $$$$\mathrm{x}=\left(\mathrm{cos2k}\pi+\mathrm{isin2k}\pi\right)^{\frac{\mathrm{1}}{\mathrm{n}}} =\mathrm{cos}\frac{\mathrm{2k}\pi}{\mathrm{n}}+\mathrm{isin}\frac{\mathrm{2k}\pi}{\mathrm{n}}\left(\mathrm{n}\in\left\{\mathrm{0},\mathrm{1},\mathrm{2},...\mathrm{n}−\mathrm{1}\right\}\right) \\ $$$$\mathrm{weget}\:\mathrm{n}\:\mathrm{different}\:\mathrm{roots} \\ $$$$\mathrm{for}\:\mathrm{k}=\mathrm{n},\mathrm{n}+\mathrm{1},\mathrm{n}+\mathrm{2},...\:\mathrm{we}\:\mathrm{get}\:\mathrm{the}\:\mathrm{repeated}\:\mathrm{roots} \\ $$$$ \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com