
Question Number 10195 by priyank last updated on 30/Jan/17
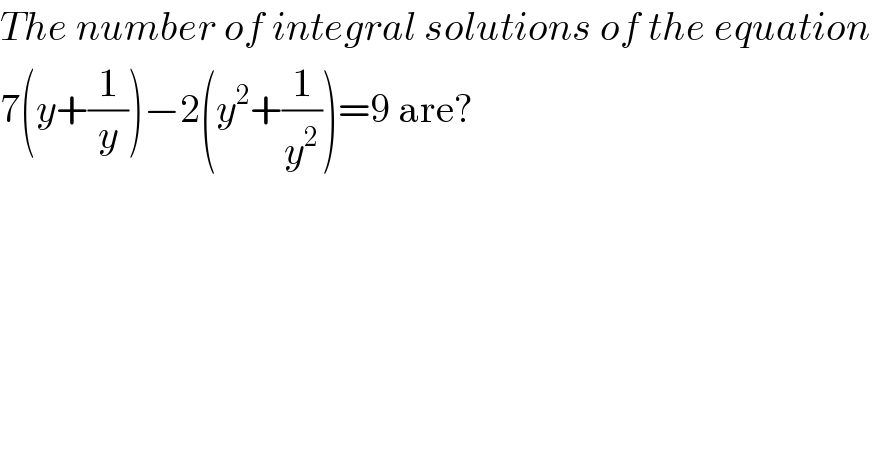
$${The}\:{number}\:{of}\:{integral}\:{solutions}\:{of}\:{the}\:{equation}\: \\ $$$$\mathrm{7}\left({y}+\frac{\mathrm{1}}{{y}}\right)−\mathrm{2}\left({y}^{\mathrm{2}} +\frac{\mathrm{1}}{{y}^{\mathrm{2}} }\right)=\mathrm{9}\:\mathrm{are}? \\ $$
Commented by prakash jain last updated on 30/Jan/17
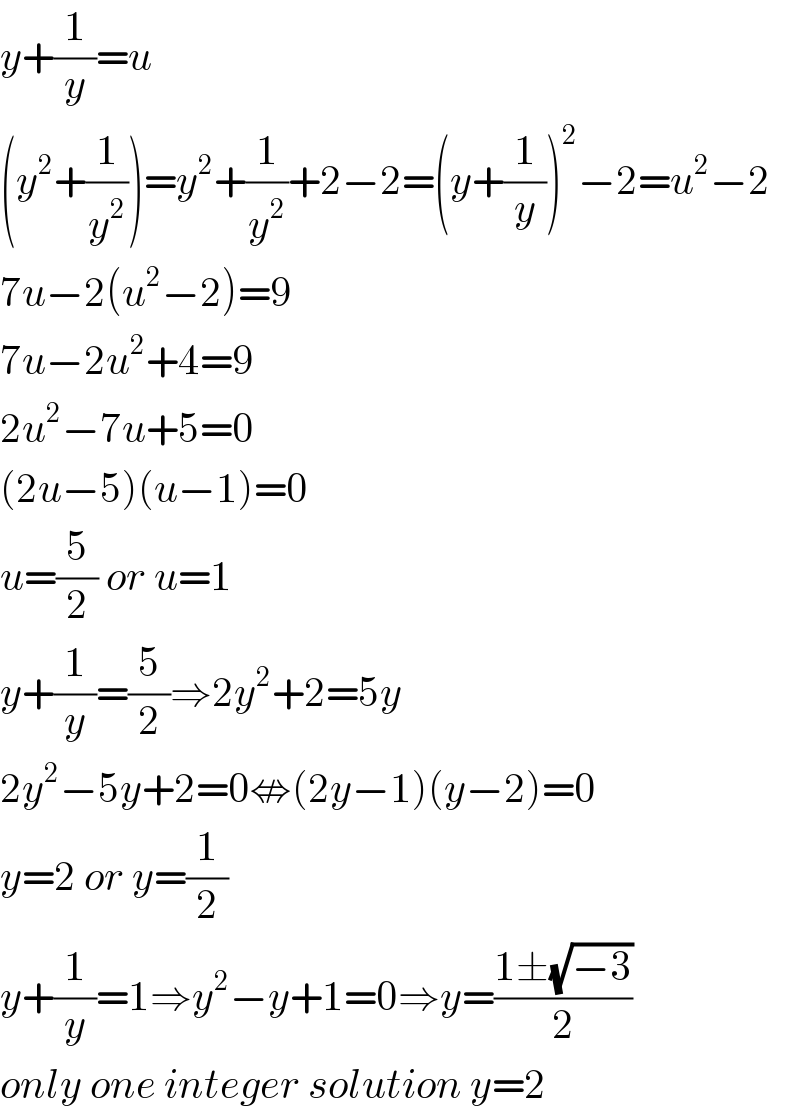
$${y}+\frac{\mathrm{1}}{{y}}={u} \\ $$$$\left({y}^{\mathrm{2}} +\frac{\mathrm{1}}{{y}^{\mathrm{2}} }\right)={y}^{\mathrm{2}} +\frac{\mathrm{1}}{{y}^{\mathrm{2}} }+\mathrm{2}−\mathrm{2}=\left({y}+\frac{\mathrm{1}}{{y}}\right)^{\mathrm{2}} −\mathrm{2}={u}^{\mathrm{2}} −\mathrm{2} \\ $$$$\mathrm{7}{u}−\mathrm{2}\left({u}^{\mathrm{2}} −\mathrm{2}\right)=\mathrm{9} \\ $$$$\mathrm{7}{u}−\mathrm{2}{u}^{\mathrm{2}} +\mathrm{4}=\mathrm{9} \\ $$$$\mathrm{2}{u}^{\mathrm{2}} −\mathrm{7}{u}+\mathrm{5}=\mathrm{0} \\ $$$$\left(\mathrm{2}{u}−\mathrm{5}\right)\left({u}−\mathrm{1}\right)=\mathrm{0} \\ $$$${u}=\frac{\mathrm{5}}{\mathrm{2}}\:{or}\:{u}=\mathrm{1} \\ $$$${y}+\frac{\mathrm{1}}{{y}}=\frac{\mathrm{5}}{\mathrm{2}}\Rightarrow\mathrm{2}{y}^{\mathrm{2}} +\mathrm{2}=\mathrm{5}{y} \\ $$$$\mathrm{2}{y}^{\mathrm{2}} −\mathrm{5}{y}+\mathrm{2}=\mathrm{0}\nLeftrightarrow\left(\mathrm{2}{y}−\mathrm{1}\right)\left({y}−\mathrm{2}\right)=\mathrm{0} \\ $$$${y}=\mathrm{2}\:{or}\:{y}=\frac{\mathrm{1}}{\mathrm{2}} \\ $$$${y}+\frac{\mathrm{1}}{{y}}=\mathrm{1}\Rightarrow{y}^{\mathrm{2}} −{y}+\mathrm{1}=\mathrm{0}\Rightarrow{y}=\frac{\mathrm{1}\pm\sqrt{−\mathrm{3}}}{\mathrm{2}} \\ $$$${only}\:{one}\:{integer}\:{solution}\:{y}=\mathrm{2} \\ $$
Answered by FilupSmith last updated on 30/Jan/17

$$\mathrm{Do}\:\mathrm{you}\:\mathrm{mean}\:\mathrm{integer}\:\mathrm{solution}? \\ $$$$\: \\ $$$$\mathrm{7}{y}+\frac{\mathrm{7}}{{y}}−\mathrm{2}{y}^{\mathrm{2}} −\frac{\mathrm{2}}{{y}^{\mathrm{2}} }=\mathrm{9} \\ $$$$\mathrm{7}{y}^{\mathrm{3}} +\mathrm{7}{y}−\mathrm{2}{y}^{\mathrm{4}} −\mathrm{2}=\mathrm{9}{y}^{\mathrm{2}} \\ $$$$−\mathrm{2}{y}^{\mathrm{4}} +\mathrm{7}{y}^{\mathrm{3}} −\mathrm{9}{y}^{\mathrm{2}} +\mathrm{7}{y}−\mathrm{2}=\mathrm{0} \\ $$$$\mathrm{2}{y}^{\mathrm{4}} −\mathrm{7}{y}^{\mathrm{3}} +\mathrm{9}{y}^{\mathrm{2}} −\mathrm{7}{y}+\mathrm{2}=\mathrm{0} \\ $$$$\left(\mathrm{2}{y}−\mathrm{1}\right)\left({y}−\mathrm{2}\right)\left({y}^{\mathrm{2}} −{y}+\mathrm{1}\right)=\mathrm{0}\:\:\:\:\:\:\left(\mathrm{from}\:\mathrm{wolfram}\:\mathrm{alpha}\right) \\ $$$$\left(\mathrm{1}\right)\:\:\:\mathrm{2}{y}=\mathrm{1}\:\Rightarrow\:{y}=\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\left(\mathrm{2}\right)\:\:\:{y}=\mathrm{2} \\ $$$$\left(\mathrm{3}\right)\:\:\:{y}=\frac{\mathrm{1}\pm{i}\sqrt{\mathrm{3}}}{\mathrm{2}} \\ $$$$\: \\ $$$$\therefore\:{y}\:\mathrm{has}\:\mathrm{1}\:\mathrm{integer}\:\mathrm{root} \\ $$
