Question Number 101959 by MathQoutes last updated on 05/Jul/20

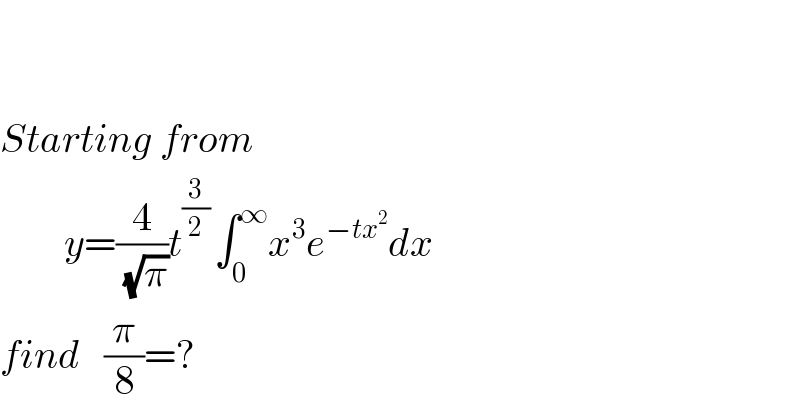
Starting from y=(4/(√π))t^((3/2) ) ∫_0 ^∞ x^3 e^(−tx^2 ) dx find (π/8)=?

Answered by mathmax by abdo last updated on 06/Jul/20

the question is not clear let find y(t) =(4/(√π))t^(3/2) ∫_0 ^∞ x^3 e^(−tx^2 ) dx for t>0 we do the changement x(√t)=u ⇒ y(t) =(4/(√π))t^(3/2) ∫_0 ^∞ ((u/(√t)))^(3 ) e^(−u^2 ) (du/(√t)) =(4/(√(πt))) ∫_0 ^∞ u^3 e^(−u^2 ) du =_(u = (√z)) (4/(√(πt))) ∫_0 ^∞ z^(3/2) e^(−z) (dz/(2(√z))) =(2/(√(πt)))∫_0 ^∞ z e^(−z) dz we know Γ(z) =∫_0 ^∞ z^(x−1) e^(−z) dt ⇒∫_0 ^∞ z e^(−z ) dz =Γ(2) =1!=1 ⇒y(t) =(2/(√(πt)))