Question and Answers Forum

All Questions      Topic List

Limits Questions

Previous in All Question      Next in All Question      

Previous in Limits      Next in Limits      

Question Number 101981 by Rohit@Thakur last updated on 05/Jul/20

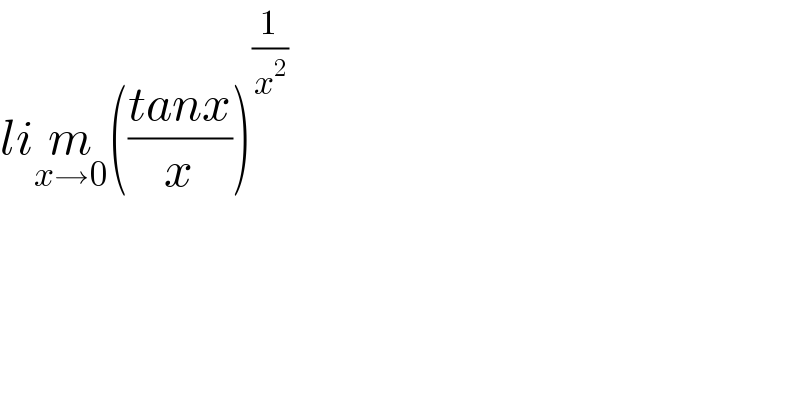
lim_(x→0) (((tanx)/x))^(1/x^2 )

$${li}\underset{{x}\rightarrow\mathrm{0}} {{m}}\left(\frac{{tanx}}{{x}}\right)^{\frac{\mathrm{1}}{{x}^{\mathrm{2}} }} \\ $$

Answered by Dwaipayan Shikari last updated on 06/Jul/20

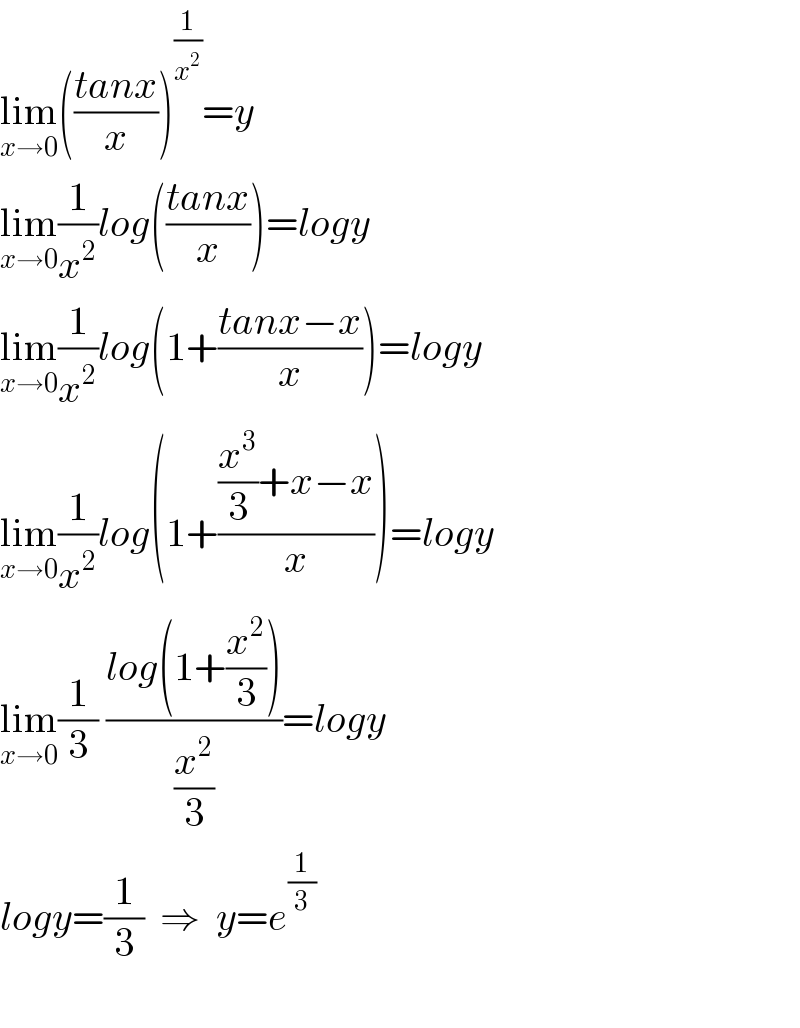
lim_(x→0) (((tanx)/x))^(1/x^2 ) =y lim_(x→0) (1/x^2 )log(((tanx)/x))=logy lim_(x→0) (1/x^2 )log(1+((tanx−x)/x))=logy lim_(x→0) (1/x^2 )log(1+(((x^3 /3)+x−x)/x))=logy lim_(x→0) (1/3) ((log(1+(x^2 /3)))/(x^2 /3))=logy logy=(1/3) ⇒ y=e^(1/3)

$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\left(\frac{{tanx}}{{x}}\right)^{\frac{\mathrm{1}}{{x}^{\mathrm{2}} }} ={y} \\ $$$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{1}}{{x}^{\mathrm{2}} }{log}\left(\frac{{tanx}}{{x}}\right)={logy} \\ $$$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{1}}{{x}^{\mathrm{2}} }{log}\left(\mathrm{1}+\frac{{tanx}−{x}}{{x}}\right)={logy} \\ $$$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{1}}{{x}^{\mathrm{2}} }{log}\left(\mathrm{1}+\frac{\frac{{x}^{\mathrm{3}} }{\mathrm{3}}+{x}−{x}}{{x}}\right)={logy} \\ $$$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{1}}{\mathrm{3}}\:\frac{{log}\left(\mathrm{1}+\frac{{x}^{\mathrm{2}} }{\mathrm{3}}\right)}{\frac{{x}^{\mathrm{2}} }{\mathrm{3}}}={logy} \\ $$$${logy}=\frac{\mathrm{1}}{\mathrm{3}}\:\:\Rightarrow\:\:{y}={e}^{\frac{\mathrm{1}}{\mathrm{3}}} \\ $$$$ \\ $$

Answered by john santu last updated on 06/Jul/20

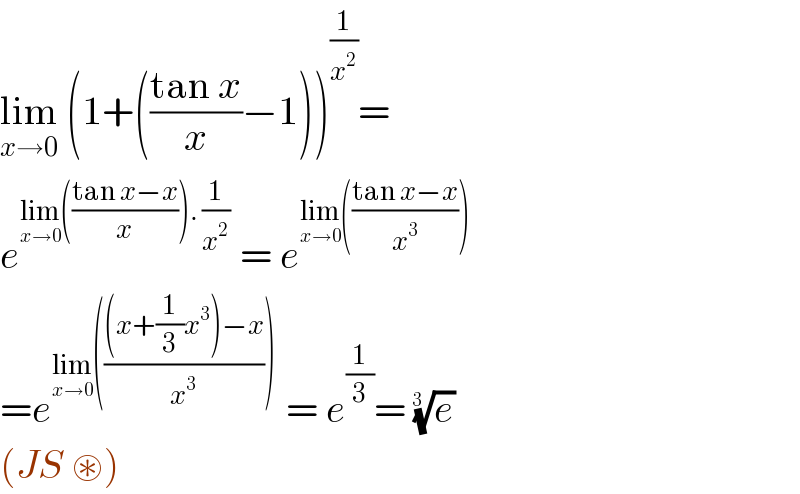
lim_(x→0) (1+(((tan x)/x)−1))^(1/x^2 ) = e^(lim_(x→0) (((tan x−x)/x)). (1/x^2 )) = e^(lim_(x→0) (((tan x−x)/x^3 ))) =e^(lim_(x→0) ((((x+(1/3)x^3 )−x)/x^3 ))) = e^(1/3) = (e)^(1/(3 )) (JS ⊛)

$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\left(\mathrm{1}+\left(\frac{\mathrm{tan}\:{x}}{{x}}−\mathrm{1}\right)\right)^{\frac{\mathrm{1}}{{x}^{\mathrm{2}} }} = \\ $$$${e}^{\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\left(\frac{\mathrm{tan}\:{x}−{x}}{{x}}\right).\:\frac{\mathrm{1}}{{x}^{\mathrm{2}} }} \:=\:{e}^{\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\left(\frac{\mathrm{tan}\:{x}−{x}}{{x}^{\mathrm{3}} }\right)} \\ $$$$={e}^{\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\left(\frac{\left({x}+\frac{\mathrm{1}}{\mathrm{3}}{x}^{\mathrm{3}} \right)−{x}}{{x}^{\mathrm{3}} }\right)} \:=\:{e}^{\frac{\mathrm{1}}{\mathrm{3}}} =\:\sqrt[{\mathrm{3}\:\:}]{{e}} \\ $$$$\left({JS}\:\circledast\right)\: \\ $$

Answered by mathmax by abdo last updated on 06/Jul/20

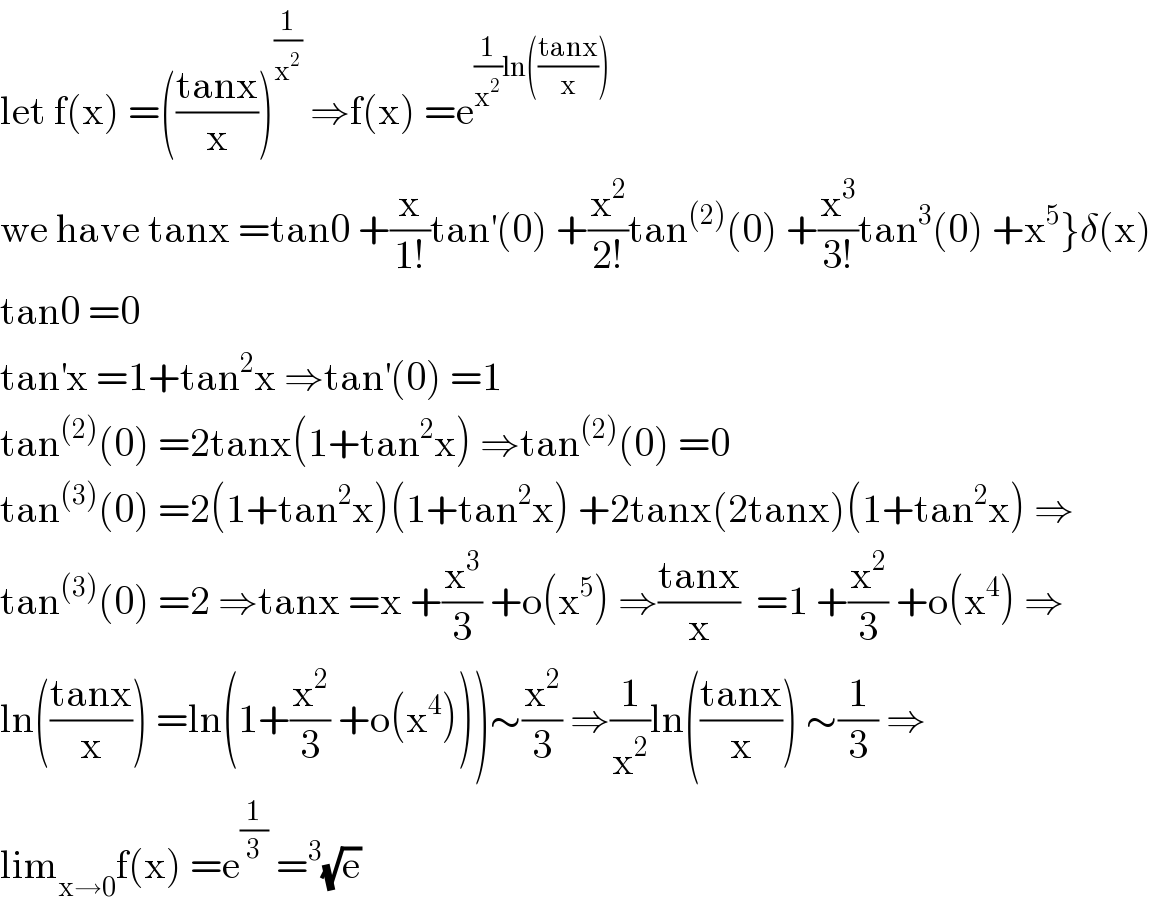
let f(x) =(((tanx)/x))^(1/x^2 ) ⇒f(x) =e^((1/x^2 )ln(((tanx)/x))) we have tanx =tan0 +(x/(1!))tan^′ (0) +(x^2 /(2!))tan^((2)) (0) +(x^3 /(3!))tan^3 (0) +x^5 }δ(x) tan0 =0 tan^′ x =1+tan^2 x ⇒tan^′ (0) =1 tan^((2)) (0) =2tanx(1+tan^2 x) ⇒tan^((2)) (0) =0 tan^((3)) (0) =2(1+tan^2 x)(1+tan^2 x) +2tanx(2tanx)(1+tan^2 x) ⇒ tan^((3)) (0) =2 ⇒tanx =x +(x^3 /3) +o(x^5 ) ⇒((tanx)/x) =1 +(x^2 /3) +o(x^4 ) ⇒ ln(((tanx)/x)) =ln(1+(x^2 /3) +o(x^4 )))∼(x^2 /3) ⇒(1/x^2 )ln(((tanx)/x)) ∼(1/3) ⇒ lim_(x→0) f(x) =e^(1/3) =^3 (√e)

$$\mathrm{let}\:\mathrm{f}\left(\mathrm{x}\right)\:=\left(\frac{\mathrm{tanx}}{\mathrm{x}}\right)^{\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{2}} }} \:\Rightarrow\mathrm{f}\left(\mathrm{x}\right)\:=\mathrm{e}^{\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{2}} }\mathrm{ln}\left(\frac{\mathrm{tanx}}{\mathrm{x}}\right)} \\ $$$$\left.\mathrm{we}\:\mathrm{have}\:\mathrm{tanx}\:=\mathrm{tan0}\:+\frac{\mathrm{x}}{\mathrm{1}!}\mathrm{tan}^{'} \left(\mathrm{0}\right)\:+\frac{\mathrm{x}^{\mathrm{2}} }{\mathrm{2}!}\mathrm{tan}^{\left(\mathrm{2}\right)} \left(\mathrm{0}\right)\:+\frac{\mathrm{x}^{\mathrm{3}} }{\mathrm{3}!}\mathrm{tan}^{\mathrm{3}} \left(\mathrm{0}\right)\:+\mathrm{x}^{\mathrm{5}} \right\}\delta\left(\mathrm{x}\right) \\ $$$$\mathrm{tan0}\:=\mathrm{0} \\ $$$$\mathrm{tan}^{'} \mathrm{x}\:=\mathrm{1}+\mathrm{tan}^{\mathrm{2}} \mathrm{x}\:\Rightarrow\mathrm{tan}^{'} \left(\mathrm{0}\right)\:=\mathrm{1} \\ $$$$\mathrm{tan}^{\left(\mathrm{2}\right)} \left(\mathrm{0}\right)\:=\mathrm{2tanx}\left(\mathrm{1}+\mathrm{tan}^{\mathrm{2}} \mathrm{x}\right)\:\Rightarrow\mathrm{tan}^{\left(\mathrm{2}\right)} \left(\mathrm{0}\right)\:=\mathrm{0} \\ $$$$\mathrm{tan}^{\left(\mathrm{3}\right)} \left(\mathrm{0}\right)\:=\mathrm{2}\left(\mathrm{1}+\mathrm{tan}^{\mathrm{2}} \mathrm{x}\right)\left(\mathrm{1}+\mathrm{tan}^{\mathrm{2}} \mathrm{x}\right)\:+\mathrm{2tanx}\left(\mathrm{2tanx}\right)\left(\mathrm{1}+\mathrm{tan}^{\mathrm{2}} \mathrm{x}\right)\:\Rightarrow \\ $$$$\mathrm{tan}^{\left(\mathrm{3}\right)} \left(\mathrm{0}\right)\:=\mathrm{2}\:\Rightarrow\mathrm{tanx}\:=\mathrm{x}\:+\frac{\mathrm{x}^{\mathrm{3}} }{\mathrm{3}}\:+\mathrm{o}\left(\mathrm{x}^{\mathrm{5}} \right)\:\Rightarrow\frac{\mathrm{tanx}}{\mathrm{x}}\:\:=\mathrm{1}\:+\frac{\mathrm{x}^{\mathrm{2}} }{\mathrm{3}}\:+\mathrm{o}\left(\mathrm{x}^{\mathrm{4}} \right)\:\Rightarrow \\ $$$$\left.\mathrm{ln}\left(\frac{\mathrm{tanx}}{\mathrm{x}}\right)\:=\mathrm{ln}\left(\mathrm{1}+\frac{\mathrm{x}^{\mathrm{2}} }{\mathrm{3}}\:+\mathrm{o}\left(\mathrm{x}^{\mathrm{4}} \right)\right)\right)\sim\frac{\mathrm{x}^{\mathrm{2}} }{\mathrm{3}}\:\Rightarrow\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{2}} }\mathrm{ln}\left(\frac{\mathrm{tanx}}{\mathrm{x}}\right)\:\sim\frac{\mathrm{1}}{\mathrm{3}}\:\Rightarrow \\ $$$$\mathrm{lim}_{\mathrm{x}\rightarrow\mathrm{0}} \mathrm{f}\left(\mathrm{x}\right)\:=\mathrm{e}^{\frac{\mathrm{1}}{\mathrm{3}}} \:=^{\mathrm{3}} \sqrt{\mathrm{e}} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com