Question Number 102001 by hardylanes last updated on 06/Jul/20

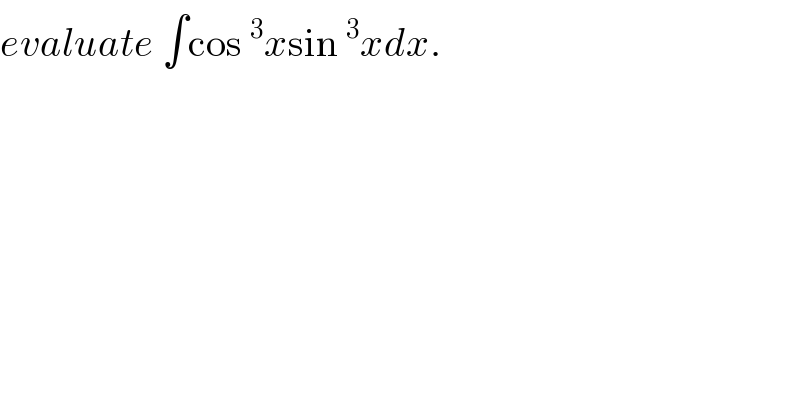
evaluate ∫cos ^3 xsin ^3 xdx.

Answered by bobhans last updated on 06/Jul/20

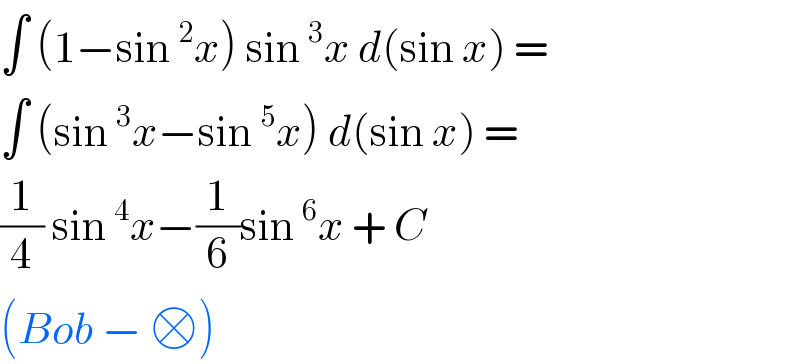
∫ (1−sin ^2 x) sin ^3 x d(sin x) = ∫ (sin ^3 x−sin ^5 x) d(sin x) = (1/4) sin ^4 x−(1/6)sin ^6 x + C (Bob − □)

Commented byhardylanes last updated on 06/Jul/20

that's it??

Commented bybobhans last updated on 06/Jul/20

what?

Answered by bobhans last updated on 06/Jul/20

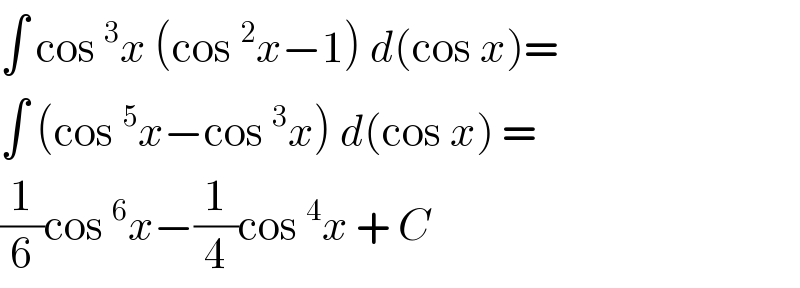
∫ cos ^3 x (cos ^2 x−1) d(cos x)= ∫ (cos ^5 x−cos ^3 x) d(cos x) = (1/6)cos ^6 x−(1/4)cos ^4 x + C