
Question Number 102020 by Dwaipayan Shikari last updated on 06/Jul/20
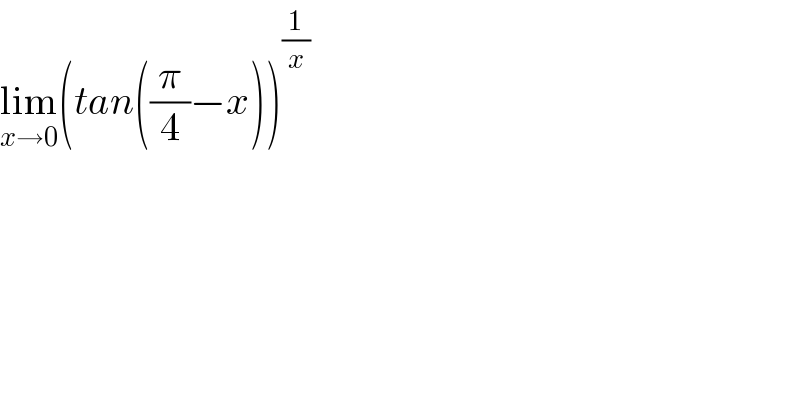
$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\left({tan}\left(\frac{\pi}{\mathrm{4}}−{x}\right)\right)^{\frac{\mathrm{1}}{{x}}} \\ $$
Answered by john santu last updated on 06/Jul/20
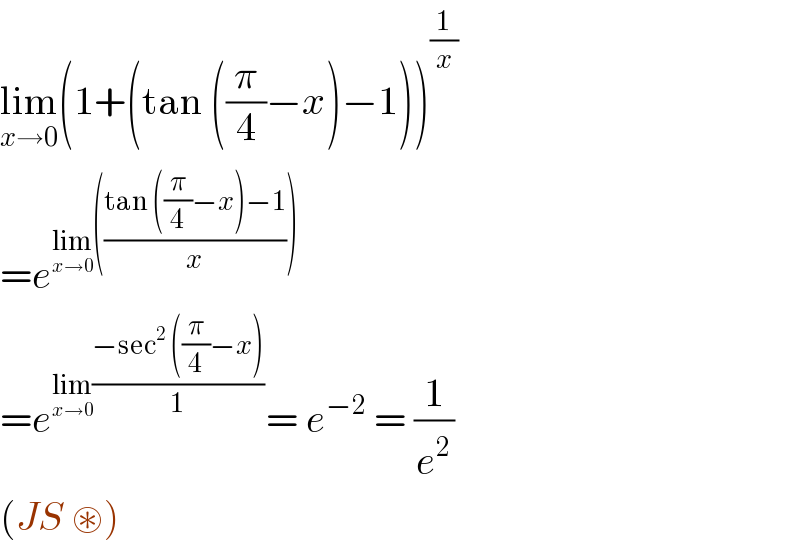
$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\left(\mathrm{1}+\left(\mathrm{tan}\:\left(\frac{\pi}{\mathrm{4}}−{x}\right)−\mathrm{1}\right)\right)^{\frac{\mathrm{1}}{{x}}} \\ $$$$={e}^{\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\left(\frac{\mathrm{tan}\:\left(\frac{\pi}{\mathrm{4}}−{x}\right)−\mathrm{1}}{{x}}\right)} \\ $$$$={e}^{\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{−\mathrm{sec}^{\mathrm{2}} \:\left(\frac{\pi}{\mathrm{4}}−{x}\right)}{\mathrm{1}}} =\:{e}^{−\mathrm{2}} \:=\:\frac{\mathrm{1}}{{e}^{\mathrm{2}} } \\ $$$$\left({JS}\:\circledast\right) \\ $$
Answered by Ar Brandon last updated on 06/Jul/20
![Let y=lim_(x→0) [tan((π/4)−x)]^(1/x) ⇒lny=lim_(x→0) {((ln[tan((π/4)−x)])/x)} ⇒lny=lim_(x→0) {−sec((π/4)−x)cosec((π/4)−x)} =−sec((π/4))cosec((π/4))=−2 ⇒lim_(x→0) [tan((π/4)−x)]^(1/x) =(1/e^2 )](Q102024.png)
$$\mathrm{Let}\:\mathrm{y}=\underset{\mathrm{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\left[\mathrm{tan}\left(\frac{\pi}{\mathrm{4}}−\mathrm{x}\right)\right]^{\frac{\mathrm{1}}{\mathrm{x}}} \Rightarrow\mathrm{lny}=\underset{\mathrm{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\left\{\frac{\mathrm{ln}\left[\mathrm{tan}\left(\frac{\pi}{\mathrm{4}}−\mathrm{x}\right)\right]}{\mathrm{x}}\right\} \\ $$$$\Rightarrow\mathrm{lny}=\underset{\mathrm{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\left\{−\mathrm{sec}\left(\frac{\pi}{\mathrm{4}}−\mathrm{x}\right)\mathrm{cosec}\left(\frac{\pi}{\mathrm{4}}−\mathrm{x}\right)\right\} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:=−\mathrm{sec}\left(\frac{\pi}{\mathrm{4}}\right)\mathrm{cosec}\left(\frac{\pi}{\mathrm{4}}\right)=−\mathrm{2} \\ $$$$\Rightarrow\underset{\mathrm{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\left[\mathrm{tan}\left(\frac{\pi}{\mathrm{4}}−\mathrm{x}\right)\right]^{\frac{\mathrm{1}}{\mathrm{x}}} =\frac{\mathrm{1}}{\mathrm{e}^{\mathrm{2}} } \\ $$
Commented by Dwaipayan Shikari last updated on 06/Jul/20

$${Great} \\ $$
