Question Number 102115 by Dwaipayan Shikari last updated on 06/Jul/20

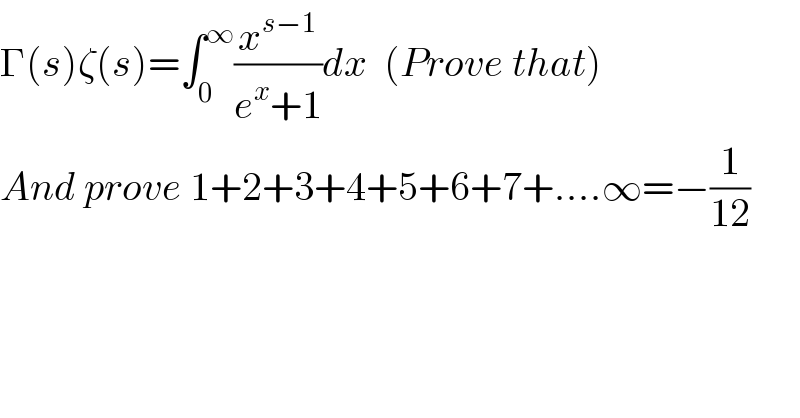
Γ(s)ζ(s)=∫_0 ^∞ (x^(s−1) /(e^x +1))dx (Prove that) And prove 1+2+3+4+5+6+7+....∞=−(1/(12))

Commented bymr W last updated on 06/Jul/20

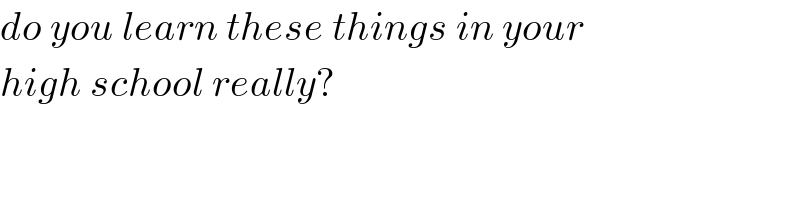
do you learn these things in your high school really?

Commented byprakash jain last updated on 07/Jul/20

The second question 1+2+3+4+...=−(1/(12)) is proved using analytical comtinuity. Search forum for analytical continuity to get same question answered earlier.

Commented byDwaipayan Shikari last updated on 07/Jul/20

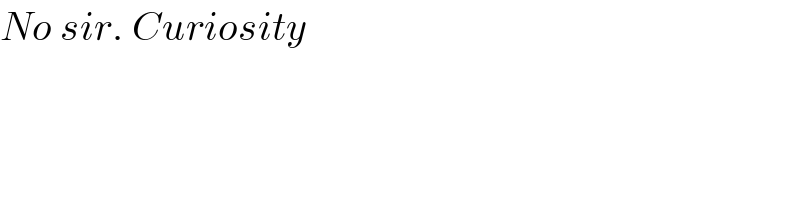
No sir. Curiosity

Answered by mathmax by abdo last updated on 06/Jul/20

the question (1)is done see the platform

Answered by mathmax by abdo last updated on 08/Jul/20

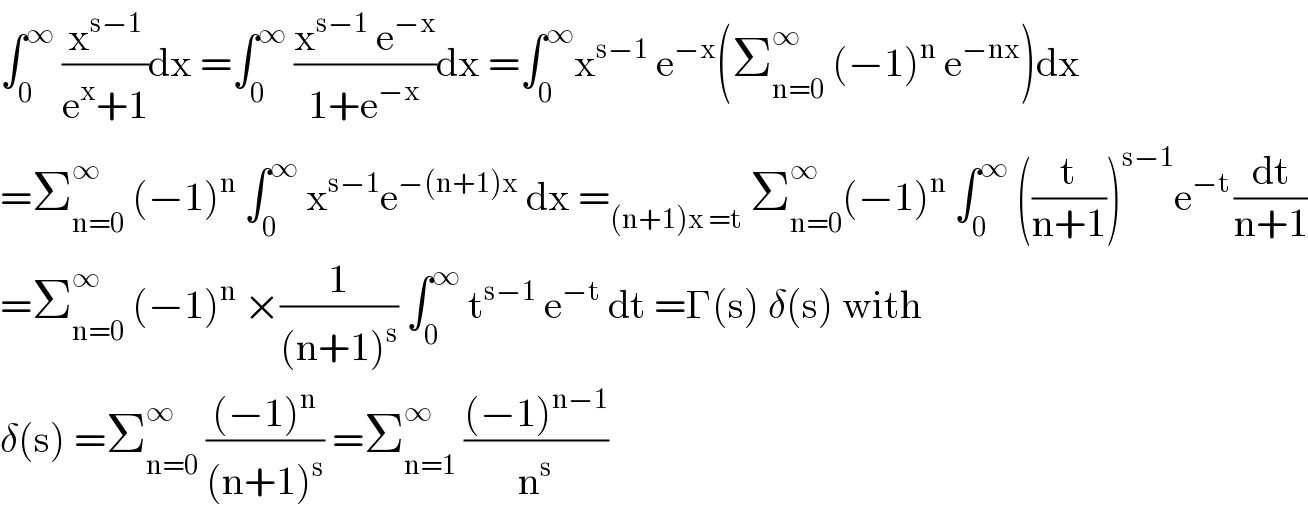
∫_0 ^∞ (x^(s−1) /(e^x +1))dx =∫_0 ^∞ ((x^(s−1) e^(−x) )/(1+e^(−x) ))dx =∫_0 ^∞ x^(s−1) e^(−x) (Σ_(n=0) ^∞ (−1)^n e^(−nx) )dx =Σ_(n=0) ^∞ (−1)^n ∫_0 ^∞ x^(s−1) e^(−(n+1)x) dx =_((n+1)x =t) Σ_(n=0) ^(∞ ) (−1)^n ∫_0 ^∞ ((t/(n+1)))^(s−1) e^(−t ) (dt/(n+1)) =Σ_(n=0) ^∞ (−1)^n ×(1/((n+1)^s )) ∫_0 ^∞ t^(s−1) e^(−t) dt =Γ(s) δ(s) with δ(s) =Σ_(n=0) ^∞ (((−1)^n )/((n+1)^s )) =Σ_(n=1) ^∞ (((−1)^(n−1) )/n^s )

Answered by mathmax by abdo last updated on 08/Jul/20

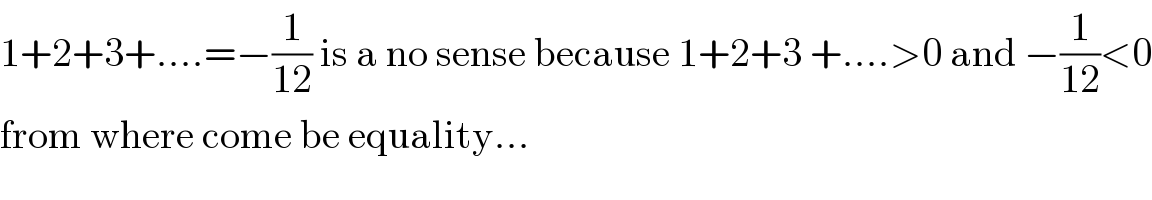
1+2+3+....=−(1/(12)) is a no sense because 1+2+3 +....>0 and −(1/(12))<0 from where come be equality...