
Question Number 102128 by Study last updated on 06/Jul/20

$$\:\int\frac{{x}+\mathrm{1}}{\sqrt{{x}}\:+\mathrm{1}}{dx}=? \\ $$
Answered by Dwaipayan Shikari last updated on 06/Jul/20
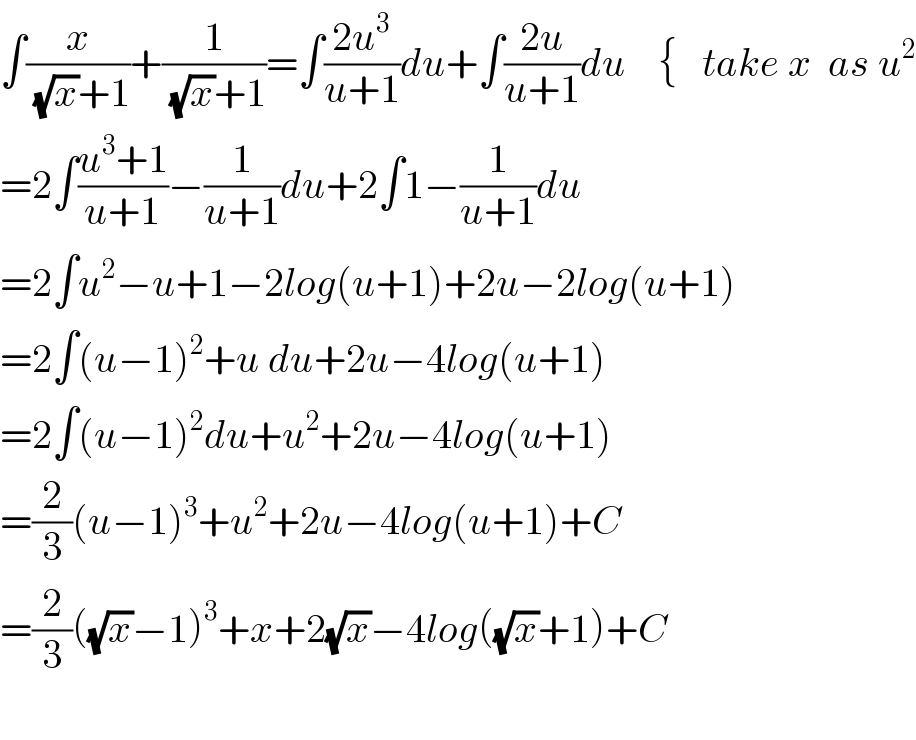
$$\int\frac{{x}}{\sqrt{{x}}+\mathrm{1}}+\frac{\mathrm{1}}{\sqrt{{x}}+\mathrm{1}}=\int\frac{\mathrm{2}{u}^{\mathrm{3}} }{{u}+\mathrm{1}}{du}+\int\frac{\mathrm{2}{u}}{{u}+\mathrm{1}}{du}\:\:\:\:\left\{\:\:\:{take}\:{x}\:\:{as}\:{u}^{\mathrm{2}} \right. \\ $$$$=\mathrm{2}\int\frac{{u}^{\mathrm{3}} +\mathrm{1}}{{u}+\mathrm{1}}−\frac{\mathrm{1}}{{u}+\mathrm{1}}{du}+\mathrm{2}\int\mathrm{1}−\frac{\mathrm{1}}{{u}+\mathrm{1}}{du} \\ $$$$=\mathrm{2}\int{u}^{\mathrm{2}} −{u}+\mathrm{1}−\mathrm{2}{log}\left({u}+\mathrm{1}\right)+\mathrm{2}{u}−\mathrm{2}{log}\left({u}+\mathrm{1}\right) \\ $$$$=\mathrm{2}\int\left({u}−\mathrm{1}\right)^{\mathrm{2}} +{u}\:{du}+\mathrm{2}{u}−\mathrm{4}{log}\left({u}+\mathrm{1}\right) \\ $$$$=\mathrm{2}\int\left({u}−\mathrm{1}\right)^{\mathrm{2}} {du}+{u}^{\mathrm{2}} +\mathrm{2}{u}−\mathrm{4}{log}\left({u}+\mathrm{1}\right) \\ $$$$=\frac{\mathrm{2}}{\mathrm{3}}\left({u}−\mathrm{1}\right)^{\mathrm{3}} +{u}^{\mathrm{2}} +\mathrm{2}{u}−\mathrm{4}{log}\left({u}+\mathrm{1}\right)+{C} \\ $$$$=\frac{\mathrm{2}}{\mathrm{3}}\left(\sqrt{{x}}−\mathrm{1}\right)^{\mathrm{3}} +{x}+\mathrm{2}\sqrt{{x}}−\mathrm{4}{log}\left(\sqrt{{x}}+\mathrm{1}\right)+{C} \\ $$$$ \\ $$
Answered by abdomathmax last updated on 06/Jul/20
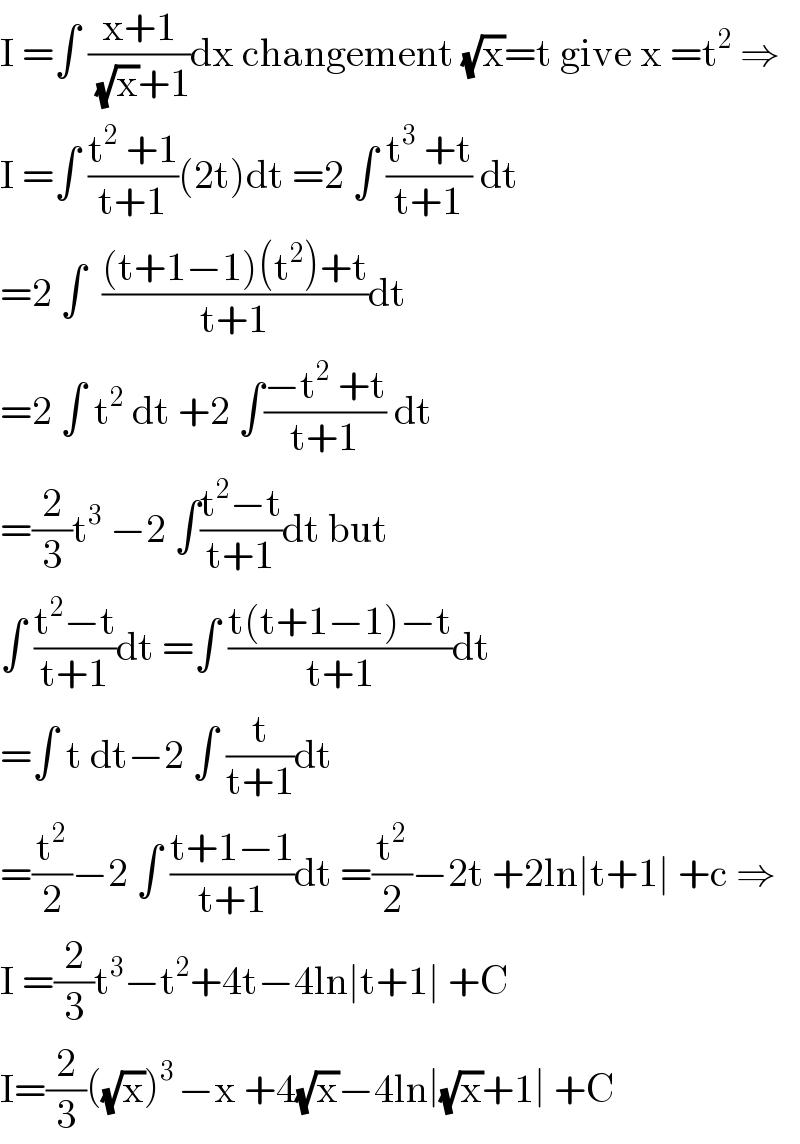
$$\mathrm{I}\:=\int\:\frac{\mathrm{x}+\mathrm{1}}{\sqrt{\mathrm{x}}+\mathrm{1}}\mathrm{dx}\:\mathrm{changement}\:\sqrt{\mathrm{x}}=\mathrm{t}\:\mathrm{give}\:\mathrm{x}\:=\mathrm{t}^{\mathrm{2}} \:\Rightarrow \\ $$$$\mathrm{I}\:=\int\:\frac{\mathrm{t}^{\mathrm{2}} \:+\mathrm{1}}{\mathrm{t}+\mathrm{1}}\left(\mathrm{2t}\right)\mathrm{dt}\:=\mathrm{2}\:\int\:\frac{\mathrm{t}^{\mathrm{3}} \:+\mathrm{t}}{\mathrm{t}+\mathrm{1}}\:\mathrm{dt} \\ $$$$=\mathrm{2}\:\int\:\:\frac{\left(\mathrm{t}+\mathrm{1}−\mathrm{1}\right)\left(\mathrm{t}^{\mathrm{2}} \right)+\mathrm{t}}{\mathrm{t}+\mathrm{1}}\mathrm{dt} \\ $$$$=\mathrm{2}\:\int\:\mathrm{t}^{\mathrm{2}} \:\mathrm{dt}\:+\mathrm{2}\:\int\frac{−\mathrm{t}^{\mathrm{2}} \:+\mathrm{t}}{\mathrm{t}+\mathrm{1}}\:\mathrm{dt} \\ $$$$=\frac{\mathrm{2}}{\mathrm{3}}\mathrm{t}^{\mathrm{3}} \:−\mathrm{2}\:\int\frac{\mathrm{t}^{\mathrm{2}} −\mathrm{t}}{\mathrm{t}+\mathrm{1}}\mathrm{dt}\:\mathrm{but} \\ $$$$\int\:\frac{\mathrm{t}^{\mathrm{2}} −\mathrm{t}}{\mathrm{t}+\mathrm{1}}\mathrm{dt}\:=\int\:\frac{\mathrm{t}\left(\mathrm{t}+\mathrm{1}−\mathrm{1}\right)−\mathrm{t}}{\mathrm{t}+\mathrm{1}}\mathrm{dt} \\ $$$$=\int\:\mathrm{t}\:\mathrm{dt}−\mathrm{2}\:\int\:\frac{\mathrm{t}}{\mathrm{t}+\mathrm{1}}\mathrm{dt} \\ $$$$=\frac{\mathrm{t}^{\mathrm{2}} }{\mathrm{2}}−\mathrm{2}\:\int\:\frac{\mathrm{t}+\mathrm{1}−\mathrm{1}}{\mathrm{t}+\mathrm{1}}\mathrm{dt}\:=\frac{\mathrm{t}^{\mathrm{2}} }{\mathrm{2}}−\mathrm{2t}\:+\mathrm{2ln}\mid\mathrm{t}+\mathrm{1}\mid\:+\mathrm{c}\:\Rightarrow \\ $$$$\mathrm{I}\:=\frac{\mathrm{2}}{\mathrm{3}}\mathrm{t}^{\mathrm{3}} −\mathrm{t}^{\mathrm{2}} +\mathrm{4t}−\mathrm{4ln}\mid\mathrm{t}+\mathrm{1}\mid\:+\mathrm{C} \\ $$$$\mathrm{I}=\frac{\mathrm{2}}{\mathrm{3}}\left(\sqrt{\mathrm{x}}\right)^{\mathrm{3}\:} −\mathrm{x}\:+\mathrm{4}\sqrt{\mathrm{x}}−\mathrm{4ln}\mid\sqrt{\mathrm{x}}+\mathrm{1}\mid\:+\mathrm{C} \\ $$
Commented by mathmax by abdo last updated on 06/Jul/20
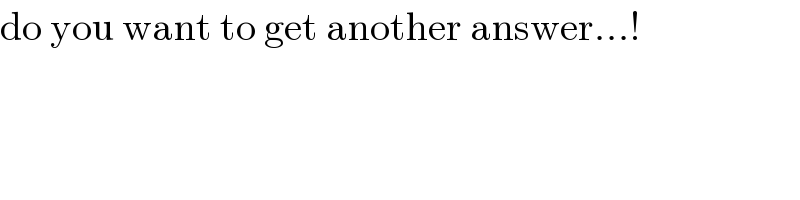
$$\mathrm{do}\:\mathrm{you}\:\mathrm{want}\:\mathrm{to}\:\mathrm{get}\:\mathrm{another}\:\mathrm{answer}...! \\ $$
Commented by Dwaipayan Shikari last updated on 07/Jul/20

$${Sorry}\:{sir}!\: \\ $$
Answered by Ar Brandon last updated on 06/Jul/20
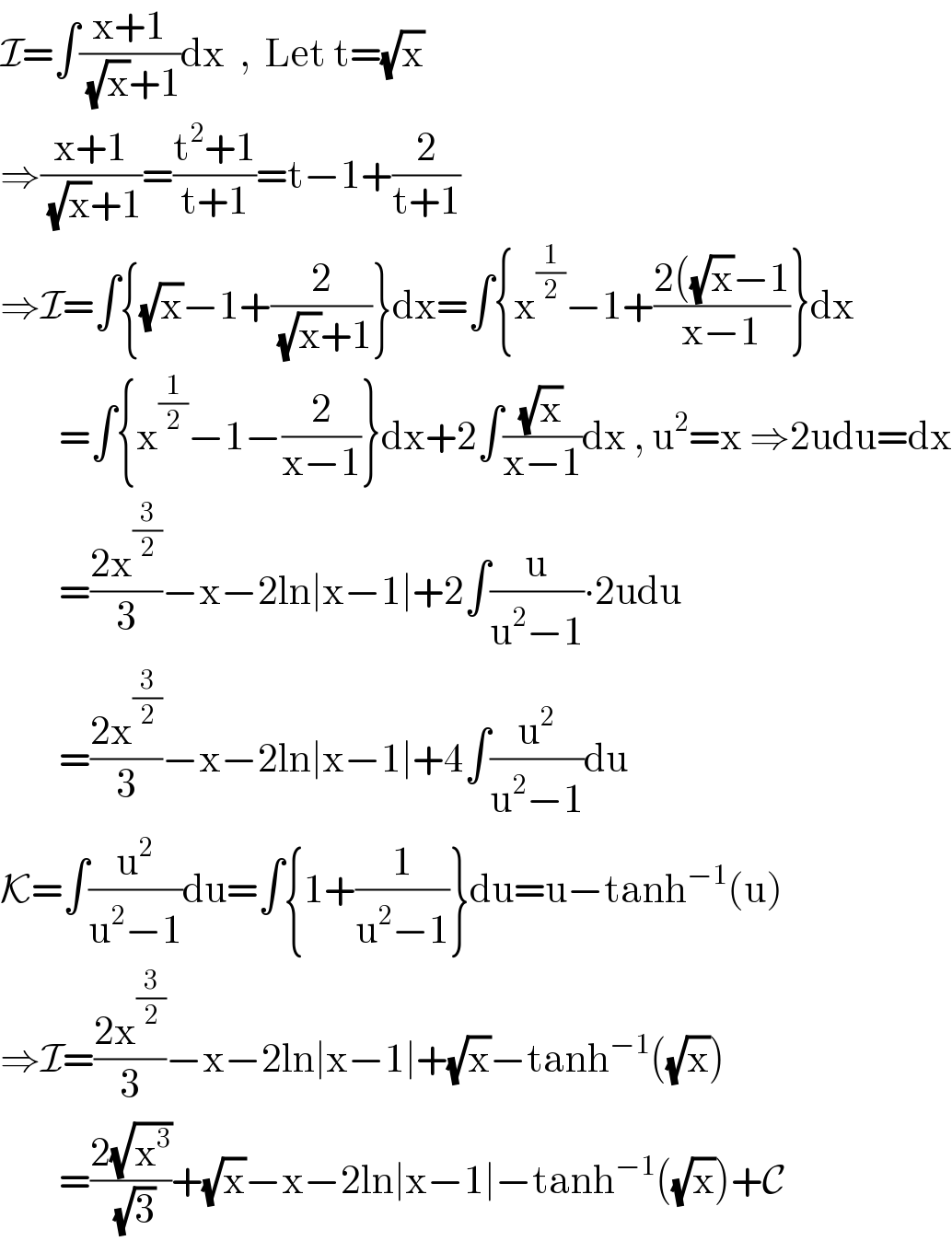
$$\mathcal{I}=\int\frac{\mathrm{x}+\mathrm{1}}{\sqrt{\mathrm{x}}+\mathrm{1}}\mathrm{dx}\:\:,\:\:\mathrm{Let}\:\mathrm{t}=\sqrt{\mathrm{x}} \\ $$$$\Rightarrow\frac{\mathrm{x}+\mathrm{1}}{\sqrt{\mathrm{x}}+\mathrm{1}}=\frac{\mathrm{t}^{\mathrm{2}} +\mathrm{1}}{\mathrm{t}+\mathrm{1}}=\mathrm{t}−\mathrm{1}+\frac{\mathrm{2}}{\mathrm{t}+\mathrm{1}} \\ $$$$\Rightarrow\mathcal{I}=\int\left\{\sqrt{\mathrm{x}}−\mathrm{1}+\frac{\mathrm{2}}{\sqrt{\mathrm{x}}+\mathrm{1}}\right\}\mathrm{dx}=\int\left\{\mathrm{x}^{\frac{\mathrm{1}}{\mathrm{2}}} −\mathrm{1}+\frac{\mathrm{2}\left(\sqrt{\mathrm{x}}−\mathrm{1}\right.}{\mathrm{x}−\mathrm{1}}\right\}\mathrm{dx} \\ $$$$\:\:\:\:\:\:\:\:=\int\left\{\mathrm{x}^{\frac{\mathrm{1}}{\mathrm{2}}} −\mathrm{1}−\frac{\mathrm{2}}{\mathrm{x}−\mathrm{1}}\right\}\mathrm{dx}+\mathrm{2}\int\frac{\sqrt{\mathrm{x}}}{\mathrm{x}−\mathrm{1}}\mathrm{dx}\:,\:\mathrm{u}^{\mathrm{2}} =\mathrm{x}\:\Rightarrow\mathrm{2udu}=\mathrm{dx} \\ $$$$\:\:\:\:\:\:\:\:=\frac{\mathrm{2x}^{\frac{\mathrm{3}}{\mathrm{2}}} }{\mathrm{3}}−\mathrm{x}−\mathrm{2ln}\mid\mathrm{x}−\mathrm{1}\mid+\mathrm{2}\int\frac{\mathrm{u}}{\mathrm{u}^{\mathrm{2}} −\mathrm{1}}\centerdot\mathrm{2udu} \\ $$$$\:\:\:\:\:\:\:\:=\frac{\mathrm{2x}^{\frac{\mathrm{3}}{\mathrm{2}}} }{\mathrm{3}}−\mathrm{x}−\mathrm{2ln}\mid\mathrm{x}−\mathrm{1}\mid+\mathrm{4}\int\frac{\mathrm{u}^{\mathrm{2}} }{\mathrm{u}^{\mathrm{2}} −\mathrm{1}}\mathrm{du} \\ $$$$\mathcal{K}=\int\frac{\mathrm{u}^{\mathrm{2}} }{\mathrm{u}^{\mathrm{2}} −\mathrm{1}}\mathrm{du}=\int\left\{\mathrm{1}+\frac{\mathrm{1}}{\mathrm{u}^{\mathrm{2}} −\mathrm{1}}\right\}\mathrm{du}=\mathrm{u}−\mathrm{tanh}^{−\mathrm{1}} \left(\mathrm{u}\right) \\ $$$$\Rightarrow\mathcal{I}=\frac{\mathrm{2x}^{\frac{\mathrm{3}}{\mathrm{2}}} }{\mathrm{3}}−\mathrm{x}−\mathrm{2ln}\mid\mathrm{x}−\mathrm{1}\mid+\sqrt{\mathrm{x}}−\mathrm{tanh}^{−\mathrm{1}} \left(\sqrt{\mathrm{x}}\right) \\ $$$$\:\:\:\:\:\:\:\:=\frac{\mathrm{2}\sqrt{\mathrm{x}^{\mathrm{3}} }}{\sqrt{\mathrm{3}}}+\sqrt{\mathrm{x}}−\mathrm{x}−\mathrm{2ln}\mid\mathrm{x}−\mathrm{1}\mid−\mathrm{tanh}^{−\mathrm{1}} \left(\sqrt{\mathrm{x}}\right)+\mathcal{C} \\ $$
Answered by OlafThorendsen last updated on 07/Jul/20
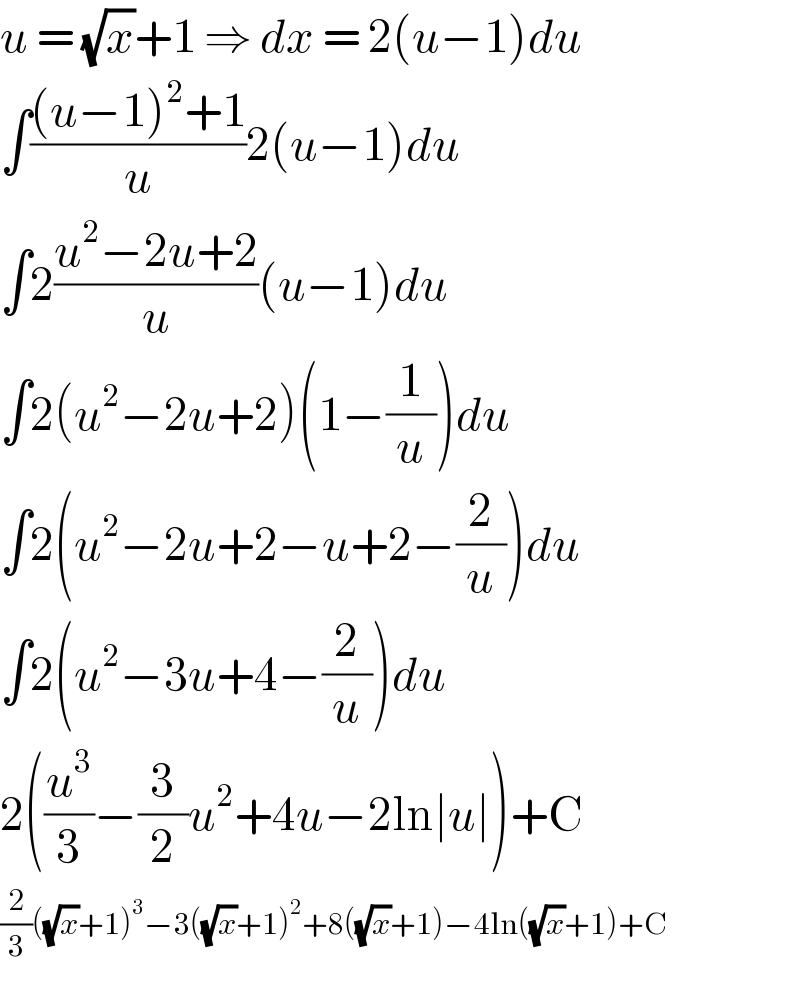
$${u}\:=\:\sqrt{{x}}+\mathrm{1}\:\Rightarrow\:{dx}\:=\:\mathrm{2}\left({u}−\mathrm{1}\right){du} \\ $$$$\int\frac{\left({u}−\mathrm{1}\right)^{\mathrm{2}} +\mathrm{1}}{{u}}\mathrm{2}\left({u}−\mathrm{1}\right){du} \\ $$$$\int\mathrm{2}\frac{{u}^{\mathrm{2}} −\mathrm{2}{u}+\mathrm{2}}{{u}}\left({u}−\mathrm{1}\right){du} \\ $$$$\int\mathrm{2}\left({u}^{\mathrm{2}} −\mathrm{2}{u}+\mathrm{2}\right)\left(\mathrm{1}−\frac{\mathrm{1}}{{u}}\right){du} \\ $$$$\int\mathrm{2}\left({u}^{\mathrm{2}} −\mathrm{2}{u}+\mathrm{2}−{u}+\mathrm{2}−\frac{\mathrm{2}}{{u}}\right){du} \\ $$$$\int\mathrm{2}\left({u}^{\mathrm{2}} −\mathrm{3}{u}+\mathrm{4}−\frac{\mathrm{2}}{{u}}\right){du} \\ $$$$\mathrm{2}\left(\frac{{u}^{\mathrm{3}} }{\mathrm{3}}−\frac{\mathrm{3}}{\mathrm{2}}{u}^{\mathrm{2}} +\mathrm{4}{u}−\mathrm{2ln}\mid{u}\mid\right)+\mathrm{C} \\ $$$$\frac{\mathrm{2}}{\mathrm{3}}\left(\sqrt{{x}}+\mathrm{1}\right)^{\mathrm{3}} −\mathrm{3}\left(\sqrt{{x}}+\mathrm{1}\right)^{\mathrm{2}} +\mathrm{8}\left(\sqrt{{x}}+\mathrm{1}\right)−\mathrm{4ln}\left(\sqrt{{x}}+\mathrm{1}\right)+\mathrm{C} \\ $$
