Question and Answers Forum

All Questions      Topic List

Integration Questions

Previous in All Question      Next in All Question      

Previous in Integration      Next in Integration      

Question Number 102163 by mathmax by abdo last updated on 07/Jul/20

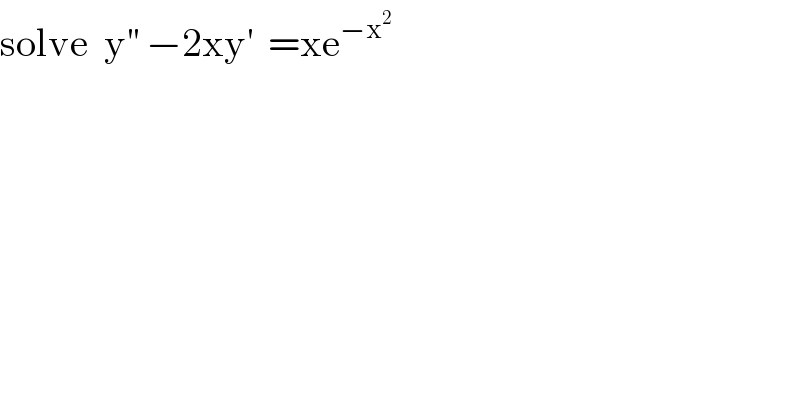
solve y^(′′) −2xy^′ =xe^(−x^2 )

$$\mathrm{solve}\:\:\mathrm{y}^{''} \:−\mathrm{2xy}^{'} \:\:=\mathrm{xe}^{−\mathrm{x}^{\mathrm{2}} } \\ $$

Answered by mathmax by abdo last updated on 08/Jul/20

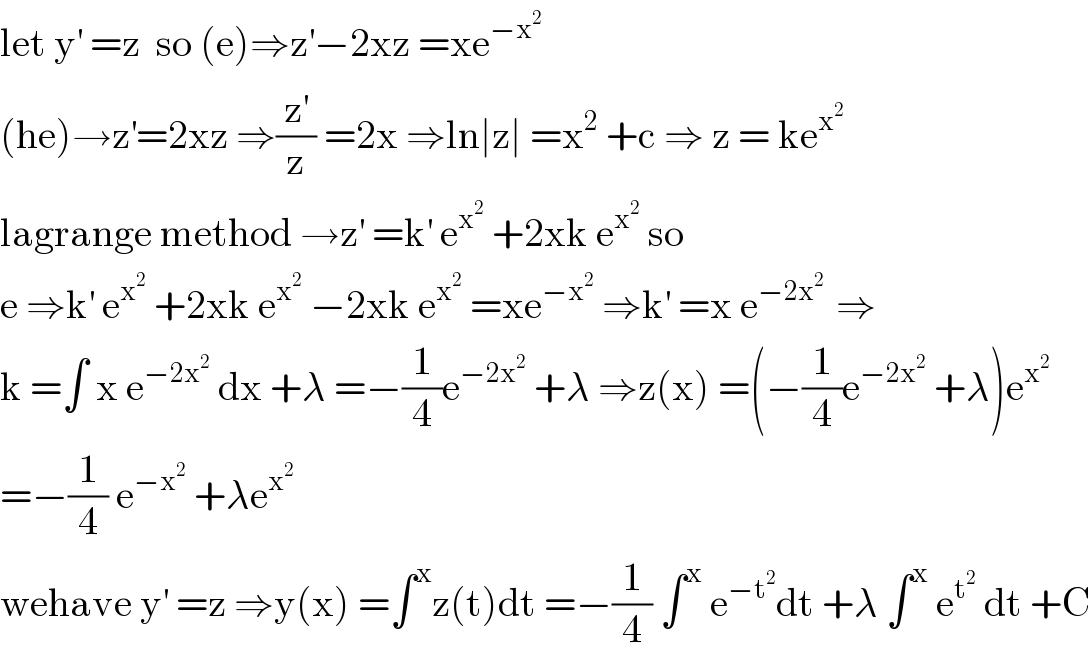
let y^′ =z so (e)⇒z^′ −2xz =xe^(−x^2 ) (he)→z^′ =2xz ⇒(z^′ /z) =2x ⇒ln∣z∣ =x^2 +c ⇒ z = ke^x^2 lagrange method →z^′ =k^′ e^x^2 +2xk e^x^2 so e ⇒k^′ e^x^2 +2xk e^x^2 −2xk e^x^2 =xe^(−x^2 ) ⇒k^′ =x e^(−2x^2 ) ⇒ k =∫ x e^(−2x^2 ) dx +λ =−(1/4)e^(−2x^2 ) +λ ⇒z(x) =(−(1/4)e^(−2x^2 ) +λ)e^x^2 =−(1/4) e^(−x^2 ) +λe^x^2 wehave y^′ =z ⇒y(x) =∫^x z(t)dt =−(1/4) ∫^x e^(−t^2 ) dt +λ ∫^x e^t^2 dt +C

$$\mathrm{let}\:\mathrm{y}^{'} \:=\mathrm{z}\:\:\mathrm{so}\:\left(\mathrm{e}\right)\Rightarrow\mathrm{z}^{'} −\mathrm{2xz}\:=\mathrm{xe}^{−\mathrm{x}^{\mathrm{2}} } \\ $$$$\left(\mathrm{he}\right)\rightarrow\mathrm{z}^{'} =\mathrm{2xz}\:\Rightarrow\frac{\mathrm{z}^{'} }{\mathrm{z}}\:=\mathrm{2x}\:\Rightarrow\mathrm{ln}\mid\mathrm{z}\mid\:=\mathrm{x}^{\mathrm{2}} \:+\mathrm{c}\:\Rightarrow\:\mathrm{z}\:=\:\mathrm{ke}^{\mathrm{x}^{\mathrm{2}} } \\ $$$$\mathrm{lagrange}\:\mathrm{method}\:\rightarrow\mathrm{z}^{'} \:=\mathrm{k}^{'} \:\mathrm{e}^{\mathrm{x}^{\mathrm{2}} } \:+\mathrm{2xk}\:\mathrm{e}^{\mathrm{x}^{\mathrm{2}} } \:\mathrm{so} \\ $$$$\mathrm{e}\:\Rightarrow\mathrm{k}^{'} \:\mathrm{e}^{\mathrm{x}^{\mathrm{2}} } \:+\mathrm{2xk}\:\mathrm{e}^{\mathrm{x}^{\mathrm{2}} } \:−\mathrm{2xk}\:\mathrm{e}^{\mathrm{x}^{\mathrm{2}} } \:=\mathrm{xe}^{−\mathrm{x}^{\mathrm{2}} } \:\Rightarrow\mathrm{k}^{'} \:=\mathrm{x}\:\mathrm{e}^{−\mathrm{2x}^{\mathrm{2}} \:} \:\Rightarrow \\ $$$$\mathrm{k}\:=\int\:\mathrm{x}\:\mathrm{e}^{−\mathrm{2x}^{\mathrm{2}} } \:\mathrm{dx}\:+\lambda\:=−\frac{\mathrm{1}}{\mathrm{4}}\mathrm{e}^{−\mathrm{2x}^{\mathrm{2}} } \:+\lambda\:\Rightarrow\mathrm{z}\left(\mathrm{x}\right)\:=\left(−\frac{\mathrm{1}}{\mathrm{4}}\mathrm{e}^{−\mathrm{2x}^{\mathrm{2}} } \:+\lambda\right)\mathrm{e}^{\mathrm{x}^{\mathrm{2}} } \\ $$$$=−\frac{\mathrm{1}}{\mathrm{4}}\:\mathrm{e}^{−\mathrm{x}^{\mathrm{2}} } \:+\lambda\mathrm{e}^{\mathrm{x}^{\mathrm{2}} } \\ $$$$\mathrm{wehave}\:\mathrm{y}^{'} \:=\mathrm{z}\:\Rightarrow\mathrm{y}\left(\mathrm{x}\right)\:=\int^{\mathrm{x}} \mathrm{z}\left(\mathrm{t}\right)\mathrm{dt}\:=−\frac{\mathrm{1}}{\mathrm{4}}\:\int^{\mathrm{x}} \:\mathrm{e}^{−\mathrm{t}^{\mathrm{2}} } \mathrm{dt}\:+\lambda\:\int^{\mathrm{x}} \:\mathrm{e}^{\mathrm{t}^{\mathrm{2}} } \:\mathrm{dt}\:+\mathrm{C} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com