Question and Answers Forum

All Questions      Topic List

Relation and Functions Questions

Previous in All Question      Next in All Question      

Previous in Relation and Functions      Next in Relation and Functions      

Question Number 102164 by mathmax by abdo last updated on 07/Jul/20

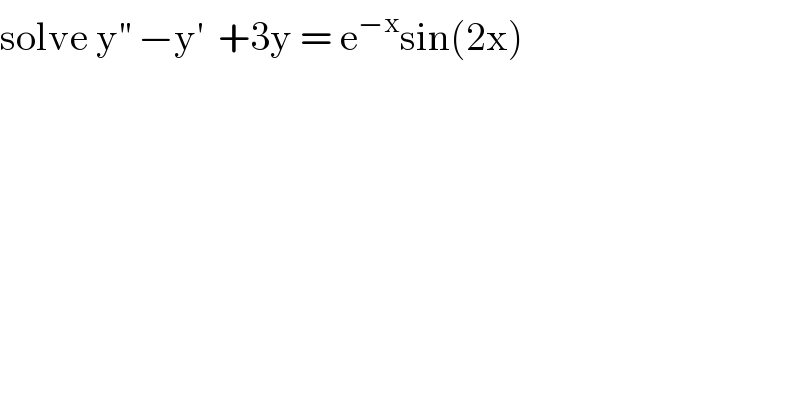
solve y^(′′) −y^′ +3y = e^(−x) sin(2x)

$$\mathrm{solve}\:\mathrm{y}^{''} \:−\mathrm{y}^{'} \:\:+\mathrm{3y}\:=\:\mathrm{e}^{−\mathrm{x}} \mathrm{sin}\left(\mathrm{2x}\right) \\ $$

Answered by mathmax by abdo last updated on 08/Jul/20

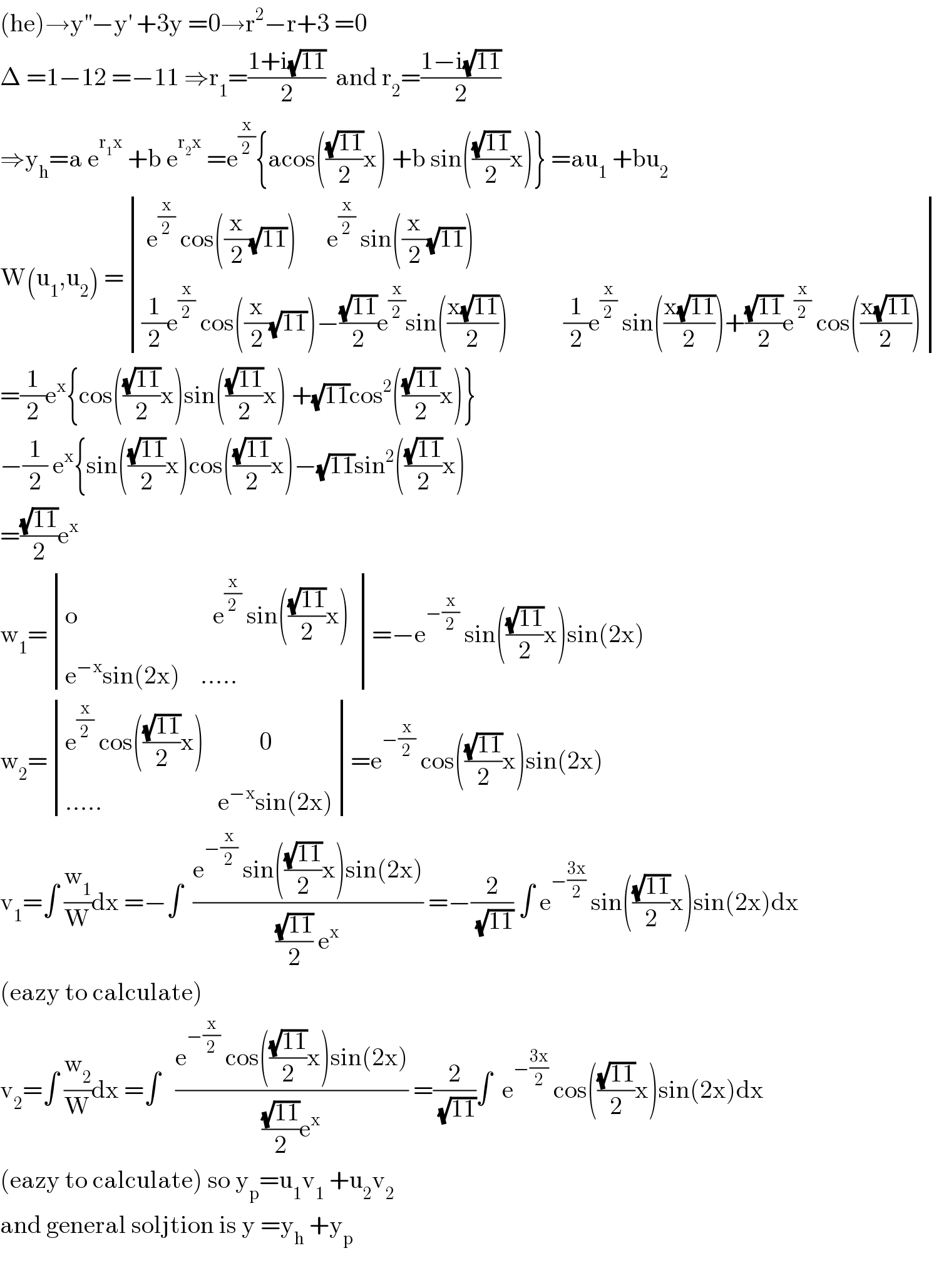
(he)→y^(′′) −y^′ +3y =0→r^2 −r+3 =0 Δ =1−12 =−11 ⇒r_1 =((1+i(√(11)))/2) and r_2 =((1−i(√(11)))/2) ⇒y_h =a e^(r_1 x) +b e^(r_2 x) =e^(x/2) {acos(((√(11))/2)x) +b sin(((√(11))/2)x)} =au_1 +bu_2 W(u_1 ,u_2 ) = determinant ((( e^(x/2) cos((x/2)(√(11))) e^(x/2) sin((x/2)(√(11))))),(((1/2)e^(x/2) cos((x/2)(√(11)))−((√(11))/2)e^(x/2) sin(((x(√(11)))/2)) (1/2)e^(x/2) sin(((x(√(11)))/2))+((√(11))/2)e^(x/2) cos(((x(√(11)))/2))))) =(1/2)e^x {cos(((√(11))/2)x)sin(((√(11))/2)x) +(√(11))cos^2 (((√(11))/2)x)} −(1/2) e^x {sin(((√(11))/2)x)cos(((√(11))/2)x)−(√(11))sin^2 (((√(11))/2)x) =((√(11))/2)e^x w_1 = determinant (((o e^(x/2) sin(((√(11))/2)x) )),((e^(−x) sin(2x) .....)))=−e^(−(x/2)) sin(((√(11))/2)x)sin(2x) w_2 = determinant (((e^(x/2) cos(((√(11))/2)x) 0)),((..... e^(−x) sin(2x))))=e^(−(x/2)) cos(((√(11))/2)x)sin(2x) v_1 =∫ (w_1 /W)dx =−∫ ((e^(−(x/2)) sin(((√(11))/2)x)sin(2x))/(((√(11))/2) e^x )) =−(2/(√(11))) ∫ e^(−((3x)/2)) sin(((√(11))/2)x)sin(2x)dx (eazy to calculate) v_2 =∫ (w_2 /W)dx =∫ ((e^(−(x/2)) cos(((√(11))/2)x)sin(2x))/(((√(11))/2)e^x )) =(2/(√(11)))∫ e^(−((3x)/2)) cos(((√(11))/2)x)sin(2x)dx (eazy to calculate) so y_p =u_1 v_1 +u_2 v_2 and general soljtion is y =y_h +y_p

$$\left(\mathrm{he}\right)\rightarrow\mathrm{y}^{''} −\mathrm{y}^{'} \:+\mathrm{3y}\:=\mathrm{0}\rightarrow\mathrm{r}^{\mathrm{2}} −\mathrm{r}+\mathrm{3}\:=\mathrm{0} \\ $$$$\Delta\:=\mathrm{1}−\mathrm{12}\:=−\mathrm{11}\:\Rightarrow\mathrm{r}_{\mathrm{1}} =\frac{\mathrm{1}+\mathrm{i}\sqrt{\mathrm{11}}}{\mathrm{2}}\:\:\mathrm{and}\:\mathrm{r}_{\mathrm{2}} =\frac{\mathrm{1}−\mathrm{i}\sqrt{\mathrm{11}}}{\mathrm{2}} \\ $$$$\Rightarrow\mathrm{y}_{\mathrm{h}} =\mathrm{a}\:\mathrm{e}^{\mathrm{r}_{\mathrm{1}} \mathrm{x}} \:+\mathrm{b}\:\mathrm{e}^{\mathrm{r}_{\mathrm{2}} \mathrm{x}} \:=\mathrm{e}^{\frac{\mathrm{x}}{\mathrm{2}}} \left\{\mathrm{acos}\left(\frac{\sqrt{\mathrm{11}}}{\mathrm{2}}\mathrm{x}\right)\:+\mathrm{b}\:\mathrm{sin}\left(\frac{\sqrt{\mathrm{11}}}{\mathrm{2}}\mathrm{x}\right)\right\}\:=\mathrm{au}_{\mathrm{1}} \:+\mathrm{bu}_{\mathrm{2}} \\ $$$$\mathrm{W}\left(\mathrm{u}_{\mathrm{1}} ,\mathrm{u}_{\mathrm{2}} \right)\:=\begin{vmatrix}{\:\mathrm{e}^{\frac{\mathrm{x}}{\mathrm{2}}} \:\mathrm{cos}\left(\frac{\mathrm{x}}{\mathrm{2}}\sqrt{\mathrm{11}}\right)\:\:\:\:\:\:\mathrm{e}^{\frac{\mathrm{x}}{\mathrm{2}}} \:\mathrm{sin}\left(\frac{\mathrm{x}}{\mathrm{2}}\sqrt{\mathrm{11}}\right)}\\{\frac{\mathrm{1}}{\mathrm{2}}\mathrm{e}^{\frac{\mathrm{x}}{\mathrm{2}}} \:\mathrm{cos}\left(\frac{\mathrm{x}}{\mathrm{2}}\sqrt{\mathrm{11}}\right)−\frac{\sqrt{\mathrm{11}}}{\mathrm{2}}\mathrm{e}^{\frac{\mathrm{x}}{\mathrm{2}}} \mathrm{sin}\left(\frac{\mathrm{x}\sqrt{\mathrm{11}}}{\mathrm{2}}\right)\:\:\:\:\:\:\:\:\:\:\:\frac{\mathrm{1}}{\mathrm{2}}\mathrm{e}^{\frac{\mathrm{x}}{\mathrm{2}}} \:\mathrm{sin}\left(\frac{\mathrm{x}\sqrt{\mathrm{11}}}{\mathrm{2}}\right)+\frac{\sqrt{\mathrm{11}}}{\mathrm{2}}\mathrm{e}^{\frac{\mathrm{x}}{\mathrm{2}}} \:\mathrm{cos}\left(\frac{\mathrm{x}\sqrt{\mathrm{11}}}{\mathrm{2}}\right)}\end{vmatrix} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\mathrm{e}^{\mathrm{x}} \left\{\mathrm{cos}\left(\frac{\sqrt{\mathrm{11}}}{\mathrm{2}}\mathrm{x}\right)\mathrm{sin}\left(\frac{\sqrt{\mathrm{11}}}{\mathrm{2}}\mathrm{x}\right)\:+\sqrt{\mathrm{11}}\mathrm{cos}^{\mathrm{2}} \left(\frac{\sqrt{\mathrm{11}}}{\mathrm{2}}\mathrm{x}\right)\right\} \\ $$$$−\frac{\mathrm{1}}{\mathrm{2}}\:\mathrm{e}^{\mathrm{x}} \left\{\mathrm{sin}\left(\frac{\sqrt{\mathrm{11}}}{\mathrm{2}}\mathrm{x}\right)\mathrm{cos}\left(\frac{\sqrt{\mathrm{11}}}{\mathrm{2}}\mathrm{x}\right)−\sqrt{\mathrm{11}}\mathrm{sin}^{\mathrm{2}} \left(\frac{\sqrt{\mathrm{11}}}{\mathrm{2}}\mathrm{x}\right)\right. \\ $$$$=\frac{\sqrt{\mathrm{11}}}{\mathrm{2}}\mathrm{e}^{\mathrm{x}} \\ $$$$\mathrm{w}_{\mathrm{1}} =\begin{vmatrix}{\mathrm{o}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{e}^{\frac{\mathrm{x}}{\mathrm{2}}} \:\mathrm{sin}\left(\frac{\sqrt{\mathrm{11}}}{\mathrm{2}}\mathrm{x}\right)\:}\\{\mathrm{e}^{−\mathrm{x}} \mathrm{sin}\left(\mathrm{2x}\right)\:\:\:\:.....}\end{vmatrix}=−\mathrm{e}^{−\frac{\mathrm{x}}{\mathrm{2}}} \:\mathrm{sin}\left(\frac{\sqrt{\mathrm{11}}}{\mathrm{2}}\mathrm{x}\right)\mathrm{sin}\left(\mathrm{2x}\right) \\ $$$$\mathrm{w}_{\mathrm{2}} =\begin{vmatrix}{\mathrm{e}^{\frac{\mathrm{x}}{\mathrm{2}}} \:\mathrm{cos}\left(\frac{\sqrt{\mathrm{11}}}{\mathrm{2}}\mathrm{x}\right)\:\:\:\:\:\:\:\:\:\:\:\mathrm{0}}\\{.....\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{e}^{−\mathrm{x}} \mathrm{sin}\left(\mathrm{2x}\right)}\end{vmatrix}=\mathrm{e}^{−\frac{\mathrm{x}}{\mathrm{2}}} \:\mathrm{cos}\left(\frac{\sqrt{\mathrm{11}}}{\mathrm{2}}\mathrm{x}\right)\mathrm{sin}\left(\mathrm{2x}\right) \\ $$$$\mathrm{v}_{\mathrm{1}} =\int\:\frac{\mathrm{w}_{\mathrm{1}} }{\mathrm{W}}\mathrm{dx}\:=−\int\:\:\frac{\mathrm{e}^{−\frac{\mathrm{x}}{\mathrm{2}}} \:\mathrm{sin}\left(\frac{\sqrt{\mathrm{11}}}{\mathrm{2}}\mathrm{x}\right)\mathrm{sin}\left(\mathrm{2x}\right)}{\frac{\sqrt{\mathrm{11}}}{\mathrm{2}}\:\mathrm{e}^{\mathrm{x}} }\:=−\frac{\mathrm{2}}{\sqrt{\mathrm{11}}}\:\int\:\mathrm{e}^{−\frac{\mathrm{3x}}{\mathrm{2}}} \:\mathrm{sin}\left(\frac{\sqrt{\mathrm{11}}}{\mathrm{2}}\mathrm{x}\right)\mathrm{sin}\left(\mathrm{2x}\right)\mathrm{dx} \\ $$$$\left(\mathrm{eazy}\:\mathrm{to}\:\mathrm{calculate}\right) \\ $$$$\mathrm{v}_{\mathrm{2}} =\int\:\frac{\mathrm{w}_{\mathrm{2}} }{\mathrm{W}}\mathrm{dx}\:=\int\:\:\:\frac{\mathrm{e}^{−\frac{\mathrm{x}}{\mathrm{2}}} \:\mathrm{cos}\left(\frac{\sqrt{\mathrm{11}}}{\mathrm{2}}\mathrm{x}\right)\mathrm{sin}\left(\mathrm{2x}\right)}{\frac{\sqrt{\mathrm{11}}}{\mathrm{2}}\mathrm{e}^{\mathrm{x}} }\:=\frac{\mathrm{2}}{\sqrt{\mathrm{11}}}\int\:\:\mathrm{e}^{−\frac{\mathrm{3x}}{\mathrm{2}}} \:\mathrm{cos}\left(\frac{\sqrt{\mathrm{11}}}{\mathrm{2}}\mathrm{x}\right)\mathrm{sin}\left(\mathrm{2x}\right)\mathrm{dx} \\ $$$$\left(\mathrm{eazy}\:\mathrm{to}\:\mathrm{calculate}\right)\:\mathrm{so}\:\mathrm{y}_{\mathrm{p}} =\mathrm{u}_{\mathrm{1}} \mathrm{v}_{\mathrm{1}} \:+\mathrm{u}_{\mathrm{2}} \mathrm{v}_{\mathrm{2}} \\ $$$$\mathrm{and}\:\mathrm{general}\:\mathrm{soljtion}\:\mathrm{is}\:\mathrm{y}\:=\mathrm{y}_{\mathrm{h}} \:+\mathrm{y}_{\mathrm{p}} \\ $$$$ \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com