
Question Number 102190 by dw last updated on 07/Jul/20
![Find the value of x ∙∙[Trigonometric Subs.] x−(x/(√(1−x^2 )))=((91)/(60))](Q102190.png)
$${Find}\:{the}\:{value}\:{of}\:\:{x}\:\centerdot\centerdot\left[{Trigonometric}\:{Subs}.\right] \\ $$$${x}−\frac{{x}}{\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }}=\frac{\mathrm{91}}{\mathrm{60}} \\ $$
Answered by bemath last updated on 07/Jul/20
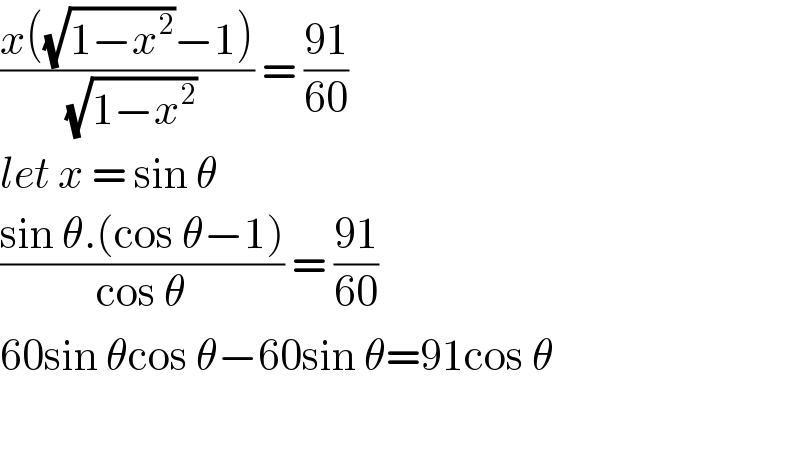
$$\frac{{x}\left(\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }−\mathrm{1}\right)}{\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }}\:=\:\frac{\mathrm{91}}{\mathrm{60}} \\ $$$${let}\:{x}\:=\:\mathrm{sin}\:\theta \\ $$$$\frac{\mathrm{sin}\:\theta.\left(\mathrm{cos}\:\theta−\mathrm{1}\right)}{\mathrm{cos}\:\theta}\:=\:\frac{\mathrm{91}}{\mathrm{60}} \\ $$$$\mathrm{60sin}\:\theta\mathrm{cos}\:\theta−\mathrm{60sin}\:\theta=\mathrm{91cos}\:\theta \\ $$$$ \\ $$
Answered by 1549442205 last updated on 07/Jul/20
![Put x=cosϕ(0≤ϕ≤π)we have cosϕ−((cosϕ)/(sinϕ))=((91)/(60))⇔60cosϕsinϕ−60cosϕ=91sinϕ(1) Put t=tan(ϕ/2).We get (1)⇔60((2(1−t^2 )t)/((1+t^2 )^2 ))−60((1−t^2 )/(1+t^2 ))=91((2t)/(1+t^2 )) ⇔120(t−t^3 )−60(1−t^4 )=182(t^3 +t) ⇔30t^4 −151t^3 −31t−30=0 ⇔30t^4 −151t^3 −31t−30=0 we get two roots(by Calculator) t_1 =−0.45781901488,t_2 =5.08098312713 From this we get ϕ_1 =2arctan t_1 =−49°11′54 (is rejected as ϕ_1 outside [0;π]) ϕ_2 =2arctan t_2 =157°43′53 Hence,x_2 =cosϕ_2 =−0.9254187445 Thus,the unique root x=−0.925417445 satisfying our prpblem](Q102248.png)
$$\mathrm{Put}\:\mathrm{x}=\mathrm{cos}\varphi\left(\mathrm{0}\leqslant\varphi\leqslant\pi\right)\mathrm{we}\:\mathrm{have}\: \\ $$$$\mathrm{cos}\varphi−\frac{\mathrm{cos}\varphi}{\mathrm{sin}\varphi}=\frac{\mathrm{91}}{\mathrm{60}}\Leftrightarrow\mathrm{60cos}\varphi\mathrm{sin}\varphi−\mathrm{60cos}\varphi=\mathrm{91sin}\varphi\left(\mathrm{1}\right) \\ $$$$\mathrm{Put}\:\mathrm{t}=\mathrm{tan}\frac{\varphi}{\mathrm{2}}.\mathrm{We}\:\mathrm{get} \\ $$$$\left(\mathrm{1}\right)\Leftrightarrow\mathrm{60}\frac{\mathrm{2}\left(\mathrm{1}−\mathrm{t}^{\mathrm{2}} \right)\mathrm{t}}{\left(\mathrm{1}+\mathrm{t}^{\mathrm{2}} \right)^{\mathrm{2}} }−\mathrm{60}\frac{\mathrm{1}−\mathrm{t}^{\mathrm{2}} }{\mathrm{1}+\mathrm{t}^{\mathrm{2}} }=\mathrm{91}\frac{\mathrm{2t}}{\mathrm{1}+\mathrm{t}^{\mathrm{2}} } \\ $$$$\Leftrightarrow\mathrm{120}\left(\mathrm{t}−\mathrm{t}^{\mathrm{3}} \right)−\mathrm{60}\left(\mathrm{1}−\mathrm{t}^{\mathrm{4}} \right)=\mathrm{182}\left(\mathrm{t}^{\mathrm{3}} +\mathrm{t}\right) \\ $$$$\Leftrightarrow\mathrm{30t}^{\mathrm{4}} −\mathrm{151t}^{\mathrm{3}} −\mathrm{31t}−\mathrm{30}=\mathrm{0} \\ $$$$\Leftrightarrow\mathrm{30t}^{\mathrm{4}} −\mathrm{151t}^{\mathrm{3}} −\mathrm{31t}−\mathrm{30}=\mathrm{0}\: \\ $$$$\mathrm{we}\:\mathrm{get}\:\mathrm{two}\:\mathrm{roots}\left(\mathrm{by}\:\mathrm{Calculator}\right) \\ $$$$\mathrm{t}_{\mathrm{1}} =−\mathrm{0}.\mathrm{45781901488},\mathrm{t}_{\mathrm{2}} =\mathrm{5}.\mathrm{08098312713} \\ $$$$\mathrm{From}\:\mathrm{this}\:\mathrm{we}\:\mathrm{get} \\ $$$$\varphi_{\mathrm{1}} =\mathrm{2arctan}\:\mathrm{t}_{\mathrm{1}} =−\mathrm{49}°\mathrm{11}'\mathrm{54}\:\left(\mathrm{is}\:\mathrm{rejected}\:\:\mathrm{as}\:\varphi_{\mathrm{1}} \mathrm{outside}\:\left[\mathrm{0};\pi\right]\right) \\ $$$$\varphi_{\mathrm{2}} =\mathrm{2arctan}\:\mathrm{t}_{\mathrm{2}} =\mathrm{157}°\mathrm{43}'\mathrm{53} \\ $$$$\mathrm{Hence},\mathrm{x}_{\mathrm{2}} =\mathrm{cos}\varphi_{\mathrm{2}} =−\mathrm{0}.\mathrm{9254187445} \\ $$$$\mathrm{Thus},\mathrm{the}\:\mathrm{unique}\:\mathrm{root}\:\boldsymbol{\mathrm{x}}=−\mathrm{0}.\mathrm{925417445} \\ $$$$\mathrm{satisfying}\:\mathrm{our}\:\mathrm{prpblem} \\ $$
