Question Number 102283 by Ar Brandon last updated on 08/Jul/20

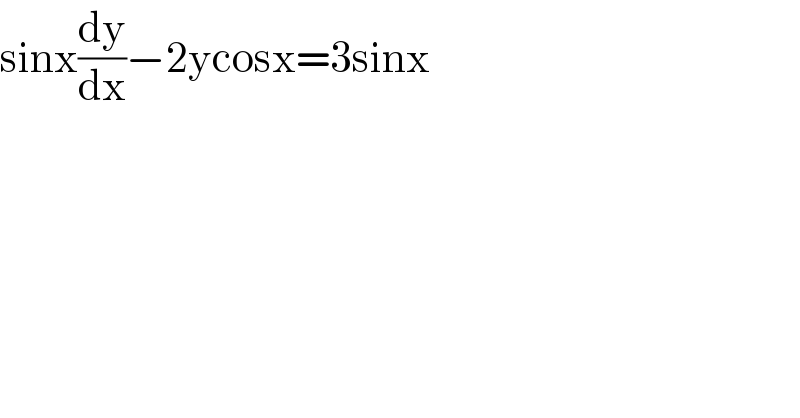
sinx(dy/dx)−2ycosx=3sinx

Answered by john santu last updated on 08/Jul/20

(dy/dx) −2cot x.y = 3 IF ⇒u(x)=e^(∫ −2cot x dx ) = e^(−2ln(sin x)) =csc^2 x ⇔y = ((∫3 csc^2 x dx + C )/(csc^2 x)) y = ((−3cot x +C)/(csc^2 x)) y = −3cot x.sin ^2 x + C.sin ^2 x (JS ⊛)

Commented byAr Brandon last updated on 08/Jul/20

Thanks Mr John

Answered by Ar Brandon last updated on 08/Jul/20

{sinx(dy/dx)−2ycosx=3sinx}∙(1/(sin^3 x)) ⇒(1/(sin^2 x))∙(dy/dx)−((2ycosx)/(sin^3 x))=(3/(sin^2 x)) ⇒d((y/(sin^2 x)))=(3/(sin^2 x))dx ⇒(y/(sin^2 x))=3∫cosec^2 xdx=−3cotx+C ⇒y=−3sinxcosx+Csin^2 x

Commented byjohn santu last updated on 08/Jul/20

great

Answered by mathmax by abdo last updated on 08/Jul/20

y^′ sinx−2ycosx =3sinx (he)→y^′ sinx =2y cosx ⇒(y^′ /y) =2((cosx)/(sinx)) ⇒ln∣y∣ =2ln∣sinx∣ +c ⇒ y =k sin^2 x mvc method give y^′ =k^′ sin^2 x +2kcosx sinx e⇒k^′ sin^3 x+2k cosx sin^2 x−2cosx)ksin^2 x =3sinx ⇒ k^′ sin^2 x =3 ⇒k^′ =(3/(sin^2 x)) ⇒ k =∫ ((3dx)/(sin^2 x)) =3 ∫ (dx/(1−(1/(tan^2 x+1)))) =3∫ ((1+tan^2 x)/(tan^2 x)) dx =_(tanx =t) 3 ∫ ((1+t^2 )/(t^2 (t^2 +1)))dt =−(3/t)+c =−(3/(tanx)) +c ⇒ y(x) =(−(3/(tanx))+c)sin^2 x =csin^2 x −((3cosx)/(sinx))sin^2 x =c sin^2 x−(3/2)sin(2x)