
Question Number 1023 by 123456 last updated on 20/May/15

$$\phi_{{n}} :\mathbb{R}\rightarrow\mathbb{R} \\ $$$${n}\in\mathbb{N}^{\ast} \\ $$$$\phi_{{n}} ={t}^{{n}} \frac{{d}^{{n}} \phi}{{dt}^{{n}} } \\ $$$$\phi_{\mathrm{1}} \left({t}\right)=?,\phi_{\mathrm{1}} \left(\mathrm{1}\right)=+\mathrm{1} \\ $$$$\phi_{\mathrm{2}} \left({t}\right)=?,\phi_{\mathrm{2}} \left(\mathrm{1}\right)=−\mathrm{1},\phi_{\mathrm{2}} ^{'} \left(\mathrm{1}\right)=+\mathrm{1} \\ $$$$\phi_{\mathrm{3}} \left({t}\right)=?,\phi_{\mathrm{3}} \left(\mathrm{1}\right)=+\mathrm{1},\phi_{\mathrm{3}} ^{'} \left(\mathrm{1}\right)=−\mathrm{1},\phi_{\mathrm{3}} ^{''} \left(\mathrm{1}\right)=+\mathrm{1} \\ $$
Commented by prakash jain last updated on 21/May/15
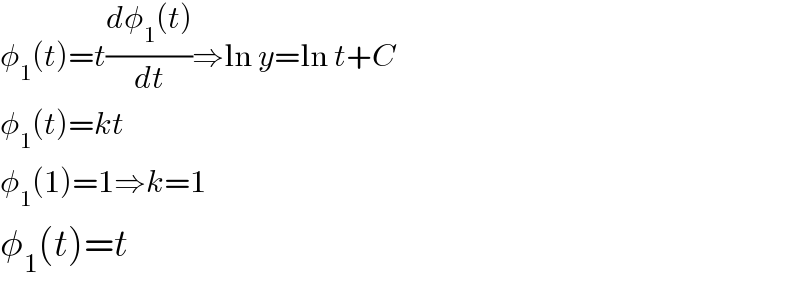
$$\phi_{\mathrm{1}} \left({t}\right)={t}\frac{{d}\phi_{\mathrm{1}} \left({t}\right)}{{dt}}\Rightarrow\mathrm{ln}\:{y}=\mathrm{ln}\:{t}+{C} \\ $$$$\phi_{\mathrm{1}} \left({t}\right)={kt} \\ $$$$\phi_{\mathrm{1}} \left(\mathrm{1}\right)=\mathrm{1}\Rightarrow{k}=\mathrm{1} \\ $$$$\phi_{\mathrm{1}} \left({t}\right)={t} \\ $$
Answered by prakash jain last updated on 21/May/15

$$\phi_{\mathrm{2}} \left({t}\right)={t}^{\mathrm{2}} \frac{{d}^{\mathrm{2}} \phi_{\mathrm{2}} }{{dt}^{\mathrm{2}} } \\ $$$${t}={e}^{{x}} \\ $$$$\frac{{d}\phi_{\mathrm{2}} }{{dt}}={e}^{−{x}} \frac{{d}\phi_{\mathrm{2}} }{{dx}},\:\frac{{d}^{\mathrm{2}} \phi_{\mathrm{2}} }{{dt}}=\left(\frac{{d}^{\mathrm{2}} \phi_{\mathrm{2}} }{{dx}^{\mathrm{2}} }−\frac{{d}\phi_{\mathrm{2}} }{{dx}}\right){e}^{−\mathrm{2}{x}} \\ $$$$\phi_{\mathrm{2}} =\phi_{\mathrm{2}} ^{''} −\phi_{\mathrm{2}} ^{'} \\ $$$$\phi_{\mathrm{2}} ^{''} −\phi_{\mathrm{2}} ^{'} −\phi_{\mathrm{2}} =\mathrm{0} \\ $$$$\mathrm{characteristic}\:\mathrm{equation} \\ $$$${r}^{\mathrm{2}} −{r}−\mathrm{1}=\mathrm{0} \\ $$$${r}_{\mathrm{1}} ,{r}_{\mathrm{2}} =\frac{\mathrm{1}\pm\sqrt{\mathrm{5}}}{\mathrm{2}} \\ $$$$\phi_{\mathrm{2}} \left({x}\right)={c}_{\mathrm{1}} {e}^{{r}_{\mathrm{1}} {x}} +{c}_{\mathrm{2}} {e}^{{r}_{\mathrm{2}} {x}} \\ $$$$\phi_{\mathrm{2}} \left({t}\right)={c}_{\mathrm{1}} {t}^{{r}_{\mathrm{1}} } +{c}_{\mathrm{2}} {t}^{{r}_{\mathrm{2}} } \\ $$$$\phi_{\mathrm{2}} \left({t}\right)=−\mathrm{1}\Rightarrow{c}_{\mathrm{1}} +{c}_{\mathrm{2}} =−\mathrm{1} \\ $$$$\phi_{\mathrm{2}} '={c}_{\mathrm{1}} {r}_{\mathrm{1}} {t}^{{r}_{\mathrm{1}} −\mathrm{1}} +{c}_{\mathrm{2}} {r}_{\mathrm{2}} {t}^{{r}_{\mathrm{2}} −\mathrm{1}} \\ $$$$\phi_{\mathrm{2}} '\left(\mathrm{1}\right)=\mathrm{1} \\ $$$$\mathrm{1}={c}_{\mathrm{1}} {r}_{\mathrm{1}} +{c}_{\mathrm{2}} {r}_{\mathrm{2}} ={c}_{\mathrm{1}} \left(\frac{\mathrm{1}+\sqrt{\mathrm{5}}}{\mathrm{2}}\right)−{c}_{\mathrm{1}} \left(\frac{\mathrm{1}−\sqrt{\mathrm{5}}}{\mathrm{2}}\right)−\frac{\mathrm{1}−\sqrt{\mathrm{5}}}{\mathrm{2}} \\ $$$$\mathrm{1}+\frac{\mathrm{1}−\sqrt{\mathrm{5}}}{\mathrm{2}}={c}_{\mathrm{1}} \sqrt{\mathrm{5}}\Rightarrow{c}_{\mathrm{1}} =\frac{\mathrm{3}−\sqrt{\mathrm{5}}}{\sqrt{\mathrm{5}}} \\ $$$${c}_{\mathrm{2}} =−\mathrm{1}−{c}_{\mathrm{1}} =−\mathrm{1}−\frac{\mathrm{3}−\sqrt{\mathrm{5}}}{\sqrt{\mathrm{5}}}=\frac{\mathrm{2}\sqrt{\mathrm{5}}−\mathrm{3}}{\mathrm{2}} \\ $$$$\phi_{\mathrm{2}} \left({t}\right)={c}_{\mathrm{1}} {x}^{{r}_{\mathrm{1}} } +{c}_{\mathrm{2}} {x}^{{r}_{\mathrm{2}} } ,\:{r}_{\mathrm{1}} =\frac{\mathrm{1}+\sqrt{\mathrm{5}}}{\mathrm{2}},\:{r}_{\mathrm{2}} =\frac{\mathrm{1}−\sqrt{\mathrm{5}}}{\mathrm{2}} \\ $$
