Question and Answers Forum

All Questions      Topic List

Integration Questions

Previous in All Question      Next in All Question      

Previous in Integration      Next in Integration      

Question Number 102313 by bemath last updated on 08/Jul/20

Answered by 1549442205 last updated on 08/Jul/20

$$\mathrm{The}\mathrm{abscissa}\mathrm{of}\mathrm{intersection}\mathrm{point}\mathrm{of}\mathrm{the}\mathrm{curve}$$$$\mathrm{y}=\frac{4}{\sqrt{\mathrm{x}}}-\frac{4}{\mathrm{x}}\mathrm{and}\mathrm{x}-\mathrm{axis}\mathrm{being}\mathrm{the}\mathrm{root}\mathrm{of}\mathrm{the}\mathrm{eqs}.\frac{4}{\sqrt{\mathrm{x}}}-\frac{4}{\mathrm{x}}=0$$$$\iff \mathrm{x}-\sqrt{\mathrm{x}}=0(\mathrm{x}\ne 0)\iff \mathrm{x}=1.\mathrm{Hence},$$$$\mathrm{S}={\int }_0^1{\mathrm{e}}^{1-\frac{1}{4}\mathrm{x}}\mathrm{dx}+{\int }_1^4[{\mathrm{e}}^{1-\frac{1}{4}\mathrm{x}}-(\frac{4}{\sqrt{\mathrm{x}}}-\frac{4}{\mathrm{x}})]\mathrm{dx}$$$${\int }_0^4{\mathrm{e}}^{1-\frac{1}{4}\mathrm{x}}\mathrm{dx}+{\int }_1^4\frac{4}{\mathrm{x}}\mathrm{dx}-{\int }_1^4\frac{4}{\sqrt{\mathrm{x}}}\mathrm{dx}$$$$=-{4\mathrm{e}}^{1-\frac{1}{4}\mathrm{x}}{\mid }_0^4+4\mathrm{lnx}{\mid }_1^4-8\sqrt{\mathrm{x}}{\stackrel{4}{\mid }}_1$$$$=-4-(-4\mathrm{e})+4(\ln 4-0)-8(2-1)$$$$=4\mathrm{e}+8\ln 2-12$$

Commented by I want to learn more last updated on 08/Jul/20

$$\mathrm{Thanks}\mathrm{sir}$$

Answered by bemath last updated on 08/Jul/20

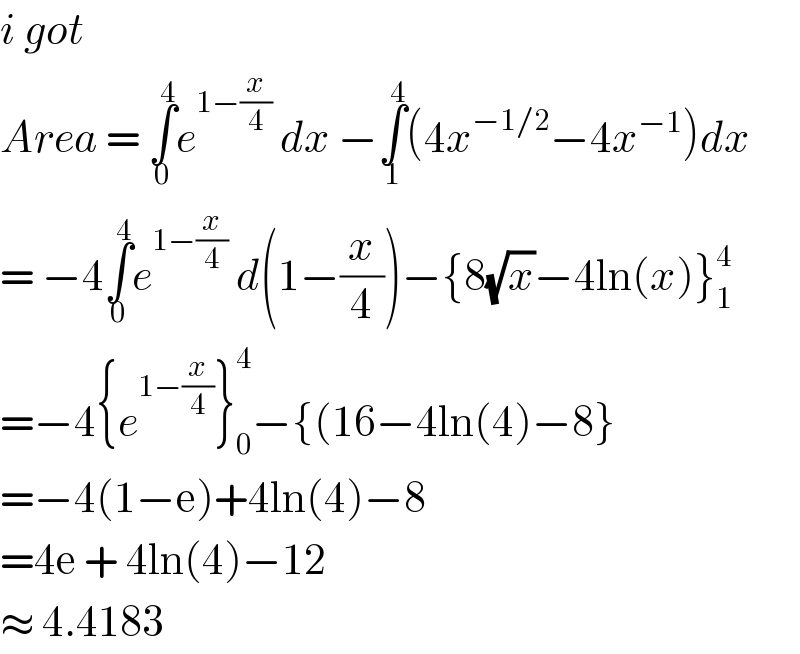
$$igot$$$$Area=\underset{0}{\stackrel{4}{\int }}{e}^{1-\frac{x}{4}}dx-\underset{1}{\stackrel{4}{\int }}(4x^{-1/2}-4x^{-1})dx$$$$=-4\underset{0}{\stackrel{4}{\int }}{e}^{1-\frac{x}{4}}d(1-\frac{x}{4})-{\{8\sqrt{x}-4\ln \left(x\right)\}}_1^4$$$$=-4{\left\{e^{1-\frac{x}{4}}\right\}}_0^4-\{(16-4\ln \left(4\right)-8\}$$$$=-4(1-\mathrm{e})+4\ln \left(4\right)-8$$$$=4\mathrm{e}+4\ln \left(4\right)-12$$$$\approx 4.4183$$

Commented by I want to learn more last updated on 08/Jul/20

$$\mathrm{Thanks}\mathrm{sir}$$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com