Question Number 102341 by Ar Brandon last updated on 08/Jul/20

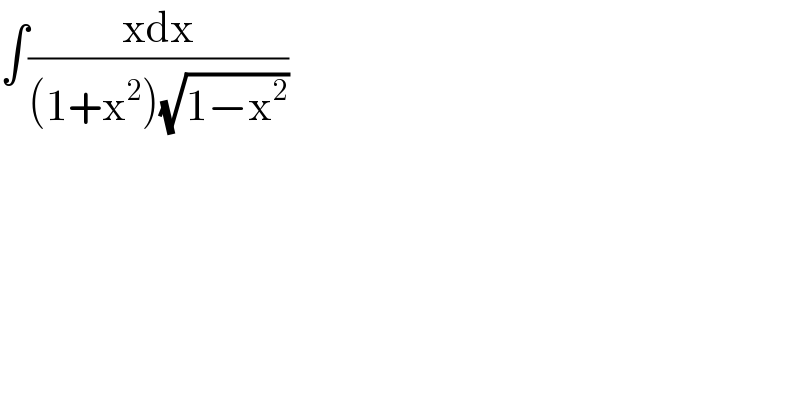
∫((xdx)/((1+x^2 )(√(1−x^2 ))))

Answered by bemath last updated on 08/Jul/20

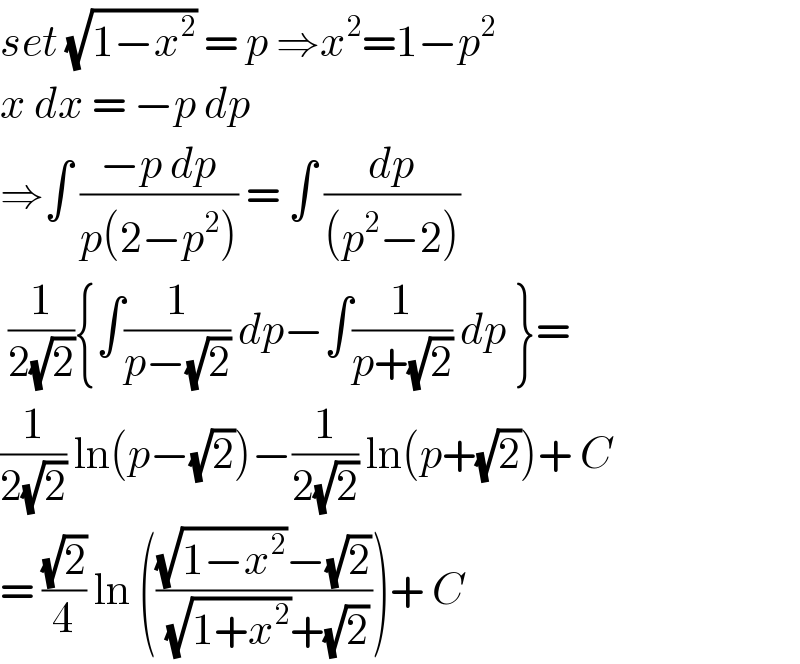
set (√(1−x^2 )) = p ⇒x^2 =1−p^2 x dx = −p dp ⇒∫ ((−p dp)/(p(2−p^2 ))) = ∫ (dp/((p^2 −2))) (1/(2(√2))){∫(1/(p−(√2))) dp−∫(1/(p+(√2))) dp }= (1/(2(√2))) ln(p−(√2))−(1/(2(√2))) ln(p+(√2))+ C = ((√2)/4) ln ((((√(1−x^2 ))−(√2))/((√(1+x^2 ))+(√2))))+ C

Answered by Dwaipayan Shikari last updated on 08/Jul/20

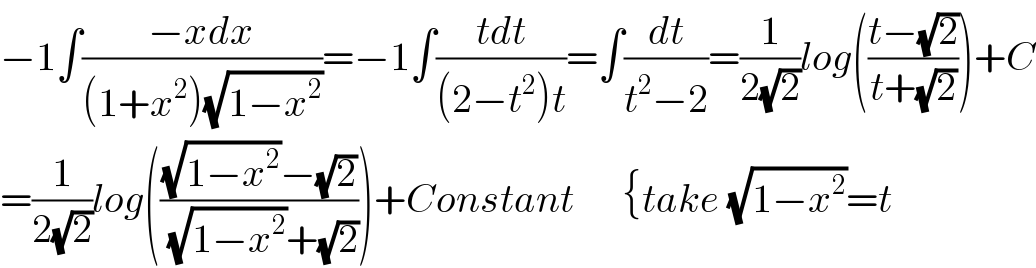
−1∫((−xdx)/((1+x^2 )(√(1−x^2 ))))=−1∫((tdt)/((2−t^2 )t))=∫(dt/(t^2 −2))=(1/(2(√2)))log(((t−(√2))/(t+(√2))))+C =(1/(2(√2)))log((((√(1−x^2 ))−(√2))/((√(1−x^2 ))+(√2))))+Constant {take (√(1−x^2 ))=t

Answered by Ar Brandon last updated on 08/Jul/20

Let x=sinθ ⇒dx=cosθdθ ⇒I=∫((sinθ)/((1+sin^2 θ)))dθ=∫((sinθdθ)/((2−cos^2 θ))) u=cosθ ⇒ du=−sinθdθ ⇒I=∫((−du)/(2−u^2 ))=−∫{((1/2(√2))/((√2)−u))+((1/2(√2))/((√2)+u))}du =−{−((√2)/4)ln∣(√2)−u∣+((√2)/4)ln∣(√2)+u∣}+C =((√2)/4)ln∣(((√2)−u)/((√2)+u))∣+C=((√2)/4)ln∣(((√2)−cosθ)/((√2)+cosθ))∣+C ⇒I=((√2)/4)ln∣(((√2)−(√(1−x^2 )))/((√2)+(√(1−x^2 ))))∣+C

Answered by mathmax by abdo last updated on 08/Jul/20

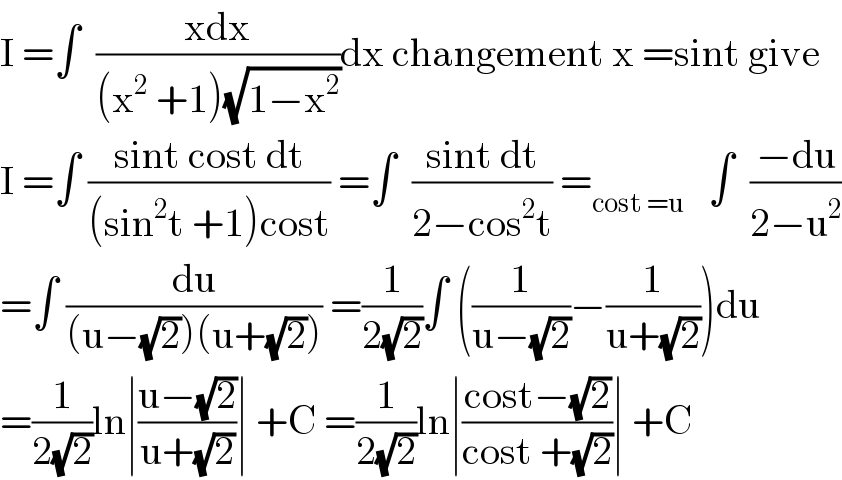
I =∫ ((xdx)/((x^2 +1)(√(1−x^2 ))))dx changement x =sint give I =∫ ((sint cost dt)/((sin^2 t +1)cost)) =∫ ((sint dt)/(2−cos^2 t)) =_(cost =u) ∫ ((−du)/(2−u^2 )) =∫ (du/((u−(√2))(u+(√2)))) =(1/(2(√2)))∫ ((1/(u−(√2)))−(1/(u+(√2))))du =(1/(2(√2)))ln∣((u−(√2))/(u+(√2)))∣ +C =(1/(2(√2)))ln∣((cost−(√2))/(cost +(√2)))∣ +C

Commented bymathmax by abdo last updated on 08/Jul/20

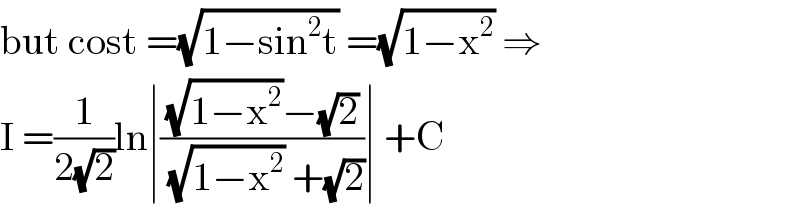
but cost =(√(1−sin^2 t)) =(√(1−x^2 )) ⇒ I =(1/(2(√2)))ln∣(((√(1−x^2 ))−(√2))/((√(1−x^2 )) +(√2)))∣ +C