Question and Answers Forum

All Questions      Topic List

None Questions

Previous in All Question      Next in All Question      

Previous in None      Next in None      

Question Number 102347 by mohammad17 last updated on 08/Jul/20

Commented by bobhans last updated on 08/Jul/20

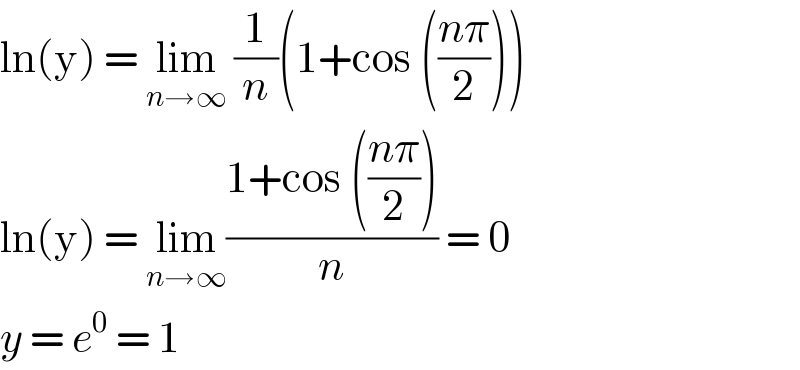
ln(y) = lim_(n→∞) (1/n)(1+cos (((nπ)/2))) ln(y) = lim_(n→∞) ((1+cos (((nπ)/2)))/n) = 0 y = e^0 = 1

$$\mathrm{ln}\left(\mathrm{y}\right)\:=\:\underset{{n}\rightarrow\infty} {\mathrm{lim}}\:\frac{\mathrm{1}}{{n}}\left(\mathrm{1}+\mathrm{cos}\:\left(\frac{{n}\pi}{\mathrm{2}}\right)\right) \\ $$$$\mathrm{ln}\left(\mathrm{y}\right)\:=\:\underset{{n}\rightarrow\infty} {\mathrm{lim}}\frac{\mathrm{1}+\mathrm{cos}\:\left(\frac{{n}\pi}{\mathrm{2}}\right)}{{n}}\:=\:\mathrm{0} \\ $$$${y}\:=\:{e}^{\mathrm{0}} \:=\:\mathrm{1} \\ $$

Commented by mohammad17 last updated on 08/Jul/20

thank you sir

$${thank}\:{you}\:{sir} \\ $$

Answered by PRITHWISH SEN 2 last updated on 08/Jul/20

let lnA=lim_(n→+∞) (1/n)ln (1+cos((nπ)/2)) = lim_(n→+∞) (1/n){cos ((nπ)/2)−(1/2)(cos ((nπ)/2))^2 +....} = 0 (as cos oscillates between finite numbers) ∴ A= 1 i.e. lim_(n→+∞) (1+cos((n𝛑)/2))^(1/n) = 1 please check

$$\mathrm{let} \\ $$$$\mathrm{lnA}=\underset{\mathrm{n}\rightarrow+\infty} {\mathrm{lim}}\:\frac{\mathrm{1}}{\mathrm{n}}\mathrm{ln}\:\left(\mathrm{1}+\mathrm{cos}\frac{\mathrm{n}\pi}{\mathrm{2}}\right) \\ $$$$\:\:\:\:\:=\:\underset{\mathrm{n}\rightarrow+\infty} {\mathrm{lim}}\:\:\frac{\mathrm{1}}{\mathrm{n}}\left\{\mathrm{cos}\:\frac{\mathrm{n}\pi}{\mathrm{2}}−\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{cos}\:\frac{\mathrm{n}\pi}{\mathrm{2}}\right)^{\mathrm{2}} +....\right\} \\ $$$$\:\:\:\:\:=\:\mathrm{0}\:\:\left(\boldsymbol{\mathrm{as}}\:\boldsymbol{\mathrm{cos}}\:\boldsymbol{\mathrm{oscillates}}\:\boldsymbol{\mathrm{between}}\:\boldsymbol{\mathrm{finite}}\:\boldsymbol{\mathrm{numbers}}\right) \\ $$$$\therefore\:\mathrm{A}=\:\mathrm{1}\: \\ $$$$\boldsymbol{\mathrm{i}}.\boldsymbol{\mathrm{e}}.\:\underset{\boldsymbol{\mathrm{n}}\rightarrow+\infty} {\mathrm{lim}}\:\left(\mathrm{1}+\boldsymbol{\mathrm{cos}}\frac{\boldsymbol{\mathrm{n}\pi}}{\mathrm{2}}\right)^{\frac{\mathrm{1}}{\boldsymbol{\mathrm{n}}}} =\:\mathrm{1}\:\boldsymbol{\mathrm{please}}\:\boldsymbol{\mathrm{check}} \\ $$

Commented by Dwaipayan Shikari last updated on 08/Jul/20

Yes it s right sir

$${Yes}\:{it}\:{s}\:{right}\:{sir}\: \\ $$

Commented by PRITHWISH SEN 2 last updated on 08/Jul/20

thank you

$$\mathrm{thank}\:\mathrm{you} \\ $$

Answered by mathmax by abdo last updated on 08/Jul/20

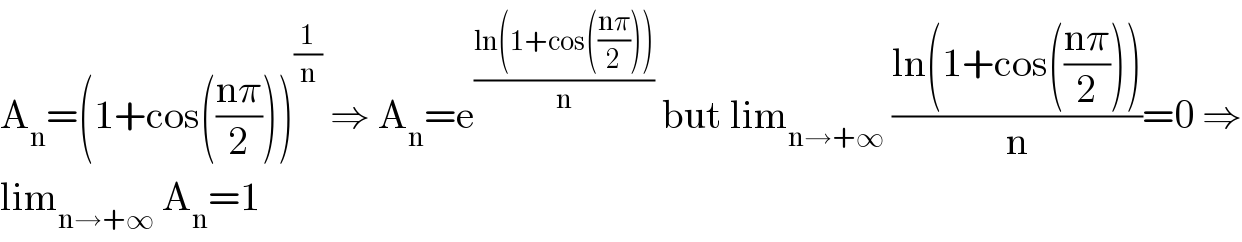
A_n =(1+cos(((nπ)/2)))^(1/n) ⇒ A_n =e^((ln(1+cos(((nπ)/2))))/n) but lim_(n→+∞) ((ln(1+cos(((nπ)/2))))/n)=0 ⇒ lim_(n→+∞) A_n =1

$$\mathrm{A}_{\mathrm{n}} =\left(\mathrm{1}+\mathrm{cos}\left(\frac{\mathrm{n}\pi}{\mathrm{2}}\right)\right)^{\frac{\mathrm{1}}{\mathrm{n}}} \:\Rightarrow\:\mathrm{A}_{\mathrm{n}} =\mathrm{e}^{\frac{\mathrm{ln}\left(\mathrm{1}+\mathrm{cos}\left(\frac{\mathrm{n}\pi}{\mathrm{2}}\right)\right)}{\mathrm{n}}} \:\mathrm{but}\:\mathrm{lim}_{\mathrm{n}\rightarrow+\infty} \:\frac{\mathrm{ln}\left(\mathrm{1}+\mathrm{cos}\left(\frac{\mathrm{n}\pi}{\mathrm{2}}\right)\right)}{\mathrm{n}}=\mathrm{0}\:\Rightarrow \\ $$$$\mathrm{lim}_{\mathrm{n}\rightarrow+\infty} \:\mathrm{A}_{\mathrm{n}} =\mathrm{1} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com