
Question Number 102366 by bobhans last updated on 08/Jul/20
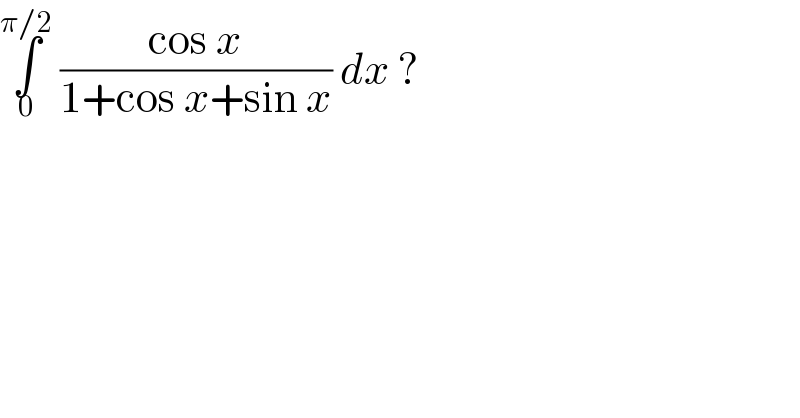
$$\underset{\mathrm{0}} {\overset{\pi/\mathrm{2}} {\int}}\:\frac{\mathrm{cos}\:{x}}{\mathrm{1}+\mathrm{cos}\:{x}+\mathrm{sin}\:{x}}\:{dx}\:? \\ $$
Answered by PRITHWISH SEN 2 last updated on 08/Jul/20

$$\mathrm{I}=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \frac{\mathrm{sin}\:\mathrm{x}}{\mathrm{1}+\mathrm{cos}\:\mathrm{x}+\mathrm{sin}\:\mathrm{x}}\mathrm{dx} \\ $$$$\mathrm{2I}=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \left\{\mathrm{1}−\frac{\mathrm{1}}{\mathrm{1}+\mathrm{cos}\:\mathrm{x}+\mathrm{sin}\:\mathrm{x}}\right\}\mathrm{dx} \\ $$$$\:\:=\:\frac{\pi}{\mathrm{2}}−\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \frac{\mathrm{sec}^{\mathrm{2}} \frac{\mathrm{x}}{\mathrm{2}}}{\mathrm{1}+\mathrm{tan}\:\frac{\mathrm{x}}{\mathrm{2}}}\mathrm{dx} \\ $$$$=\:\frac{\pi}{\mathrm{2}}−\mathrm{ln}\mid\mathrm{1}+\mathrm{tan}\:\frac{\mathrm{x}}{\mathrm{2}}\mid_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \\ $$$$=\:\frac{\pi}{\mathrm{2}}−\mathrm{ln}\mid\mathrm{2}\mid \\ $$$$\therefore\:\boldsymbol{\mathrm{I}}=\:\frac{\boldsymbol{\pi}}{\mathrm{4}}\:−\:\frac{\mathrm{1}}{\mathrm{2}}\boldsymbol{\mathrm{ln}}\mathrm{2}\:\:\:\:\:\boldsymbol{\mathrm{please}}\:\boldsymbol{\mathrm{check}} \\ $$
Commented by Dwaipayan Shikari last updated on 08/Jul/20

$${It}\:{is}\:{right} \\ $$
Commented by PRITHWISH SEN 2 last updated on 08/Jul/20
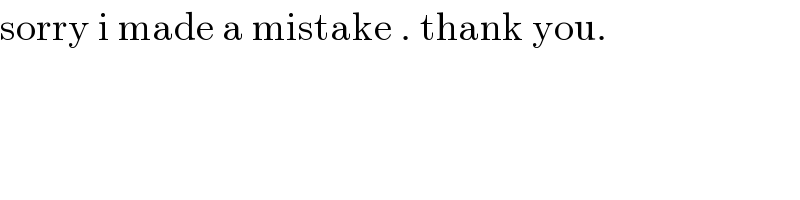
$$\mathrm{sorry}\:\mathrm{i}\:\mathrm{made}\:\mathrm{a}\:\mathrm{mistake}\:.\:\mathrm{thank}\:\mathrm{you}. \\ $$
Commented by bobhans last updated on 09/Jul/20

$${yes}\:{thank}\:{you} \\ $$
Answered by Dwaipayan Shikari last updated on 08/Jul/20
![∫_0 ^(π/2) ((cosx)/(1+cosx+sinx))=∫((sinx)/(1+cosx+sinx))=I 2I=∫_0 ^(π/2) 1−(1/(1+cosx+sinx))dx 2I=(π/2)−2∫_0 ^1 (1/(1+((1−t^2 )/(1+t^2 ))+((2t)/(1+t^2 )))).(1/(1+t^2 ))dt put tan(x/2)=t 2I=(π/2)−2∫_0 ^1 (1/(2(1+t)))dt 2I=(π/2)−[log(1+t)]_0 ^1 2I=(π/2)−log2 I=(π/4)−(1/2)log2](Q102375.png)
$$\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \frac{{cosx}}{\mathrm{1}+{cosx}+{sinx}}=\int\frac{{sinx}}{\mathrm{1}+{cosx}+{sinx}}={I} \\ $$$$\mathrm{2}{I}=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \mathrm{1}−\frac{\mathrm{1}}{\mathrm{1}+{cosx}+{sinx}}{dx} \\ $$$$\mathrm{2}{I}=\frac{\pi}{\mathrm{2}}−\mathrm{2}\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{1}}{\mathrm{1}+\frac{\mathrm{1}−{t}^{\mathrm{2}} }{\mathrm{1}+{t}^{\mathrm{2}} }+\frac{\mathrm{2}{t}}{\mathrm{1}+{t}^{\mathrm{2}} }}.\frac{\mathrm{1}}{\mathrm{1}+{t}^{\mathrm{2}} }{dt}\:\:\:\:{put}\:\:\:{tan}\frac{{x}}{\mathrm{2}}={t} \\ $$$$\mathrm{2}{I}=\frac{\pi}{\mathrm{2}}−\mathrm{2}\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{1}}{\mathrm{2}\left(\mathrm{1}+{t}\right)}{dt} \\ $$$$\mathrm{2}{I}=\frac{\pi}{\mathrm{2}}−\left[{log}\left(\mathrm{1}+{t}\right)\right]_{\mathrm{0}} ^{\mathrm{1}} \\ $$$$\mathrm{2}{I}=\frac{\pi}{\mathrm{2}}−{log}\mathrm{2} \\ $$$${I}=\frac{\pi}{\mathrm{4}}−\frac{\mathrm{1}}{\mathrm{2}}{log}\mathrm{2}\:\:\: \\ $$
Answered by mathmax by abdo last updated on 08/Jul/20
![I =∫_0 ^(π/2) ((cosx)/(1+cosx +sinx))dx cha7gement tan((x/2))=t give I =∫_0 ^1 (((1−t^2 )/(1+t^2 ))/(1+((1−t^2 )/(1+t^2 )) +((2t)/(1+t^2 ))))×((2dt)/(1+t^2 )) =2∫_0 ^1 ((1−t^2 )/((1+t^2 +1−t^2 +2t)(t^2 +1)))dt =∫_0 ^1 ((1−t^2 )/((t+1)(t^2 +1)))dt =∫_0 ^(1 ) ((1−t)/(t^2 +1))dt =∫_0 ^1 (dt/(t^2 +1)) −(1/2)∫_0 ^1 ((2t)/(t^2 +1))dt =[arctan(t)]_0 ^1 −(1/2) [ln(t^2 +1)]_0 ^1 =(π/4)−((ln(2))/2)](Q102398.png)
$$\mathrm{I}\:=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\frac{\mathrm{cosx}}{\mathrm{1}+\mathrm{cosx}\:+\mathrm{sinx}}\mathrm{dx}\:\mathrm{cha7gement}\:\mathrm{tan}\left(\frac{\mathrm{x}}{\mathrm{2}}\right)=\mathrm{t}\:\mathrm{give} \\ $$$$\mathrm{I}\:=\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\frac{\mathrm{1}−\mathrm{t}^{\mathrm{2}} }{\mathrm{1}+\mathrm{t}^{\mathrm{2}} }}{\mathrm{1}+\frac{\mathrm{1}−\mathrm{t}^{\mathrm{2}} }{\mathrm{1}+\mathrm{t}^{\mathrm{2}} }\:+\frac{\mathrm{2t}}{\mathrm{1}+\mathrm{t}^{\mathrm{2}} }}×\frac{\mathrm{2dt}}{\mathrm{1}+\mathrm{t}^{\mathrm{2}} }\:=\mathrm{2}\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\mathrm{1}−\mathrm{t}^{\mathrm{2}} }{\left(\mathrm{1}+\mathrm{t}^{\mathrm{2}} \:+\mathrm{1}−\mathrm{t}^{\mathrm{2}} \:+\mathrm{2t}\right)\left(\mathrm{t}^{\mathrm{2}} +\mathrm{1}\right)}\mathrm{dt} \\ $$$$=\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\mathrm{1}−\mathrm{t}^{\mathrm{2}} }{\left(\mathrm{t}+\mathrm{1}\right)\left(\mathrm{t}^{\mathrm{2}} +\mathrm{1}\right)}\mathrm{dt}\:=\int_{\mathrm{0}} ^{\mathrm{1}\:} \frac{\mathrm{1}−\mathrm{t}}{\mathrm{t}^{\mathrm{2}} \:+\mathrm{1}}\mathrm{dt}\:=\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\mathrm{dt}}{\mathrm{t}^{\mathrm{2}} \:+\mathrm{1}}\:−\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\mathrm{2t}}{\mathrm{t}^{\mathrm{2}} \:+\mathrm{1}}\mathrm{dt} \\ $$$$=\left[\mathrm{arctan}\left(\mathrm{t}\right)\right]_{\mathrm{0}} ^{\mathrm{1}} \:−\frac{\mathrm{1}}{\mathrm{2}}\:\left[\mathrm{ln}\left(\mathrm{t}^{\mathrm{2}} \:+\mathrm{1}\right)\right]_{\mathrm{0}} ^{\mathrm{1}} \:=\frac{\pi}{\mathrm{4}}−\frac{\mathrm{ln}\left(\mathrm{2}\right)}{\mathrm{2}} \\ $$
