Question Number 102369 by bobhans last updated on 08/Jul/20

find the area bounded inner the curve r = 4−2cos θ and outer the curve r = 6+2cos θ

Answered by Ar Brandon last updated on 08/Jul/20

Area , A=∫_0 ^(2π) ∫_(4−2cosθ) ^(6+2cosθ) rdrdθ=∫_0 ^(2π) [(r^2 /2)]_(4−2cosθ) ^(6+2cosθ) dθ ⇒A=(1/2)∫_0 ^(2π) {(6+2cosθ)^2 −(4−2cosθ)^2 }dθ =(1/2)∫_0 ^(2π) {(36+24cosθ+4cos^2 θ)−(16−16cosθ+4cos^2 θ)}dθ =(1/2)∫_0 ^(2π) (20+40cosθ)dθ=[((20θ+40sinθ)/2)]_0 ^(2π) =20π square units Don′t really know if I′ve done it in the right way. Please let me know what you think.

Commented bymr W last updated on 09/Jul/20

you are right. i misread, because this is how the question is displayed on my device:

Commented bymr W last updated on 08/Jul/20

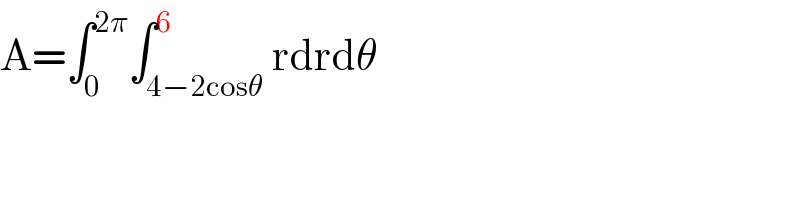
A=∫_0 ^(2π) ∫_(4−2cosθ) ^6 rdrdθ

Commented byAr Brandon last updated on 08/Jul/20

Why the 6 at the upper bound, mr W ?

Commented bymr W last updated on 09/Jul/20

Commented bymr W last updated on 09/Jul/20

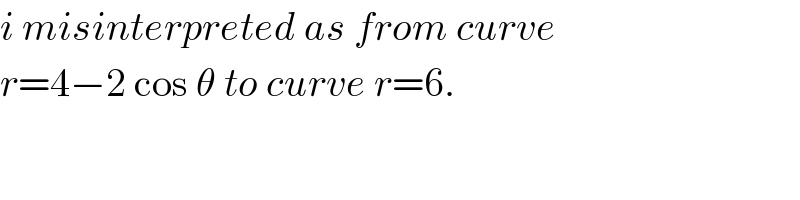
i misinterpreted as from curve r=4−2 cos θ to curve r=6.

Commented bybobhans last updated on 09/Jul/20

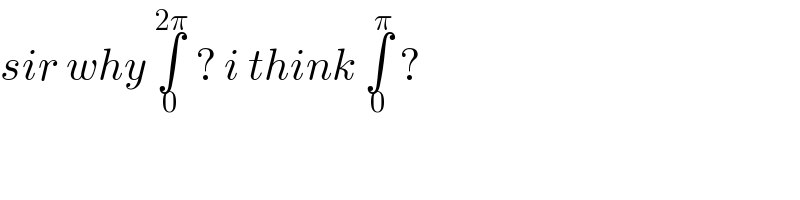
sir why ∫_0 ^(2π) ? i think ∫_0 ^π ?

Commented bybobhans last updated on 09/Jul/20

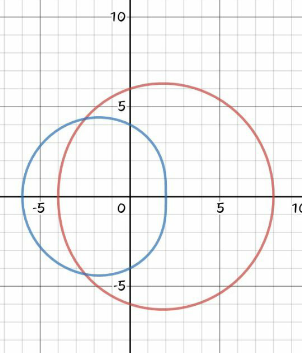
Commented byAr Brandon last updated on 09/Jul/20

OK Sir

Commented byAr Brandon last updated on 09/Jul/20

You′re heading somewhere mr Bobhans. I think you′re making a point there. Let′s see; Mathematically inner the curve 4−2cosθ implies 4−2cosθ<r and outer the curve 6+2cosθ implies 6+2cosθ>r Therefore at points of intersection r=r ⇒4−2cosθ=6+2cosθ ⇒cosθ=((−1)/2) ⇒θ_1 =(4/3)π , θ_2 =(2/3)π

Commented byAr Brandon last updated on 09/Jul/20

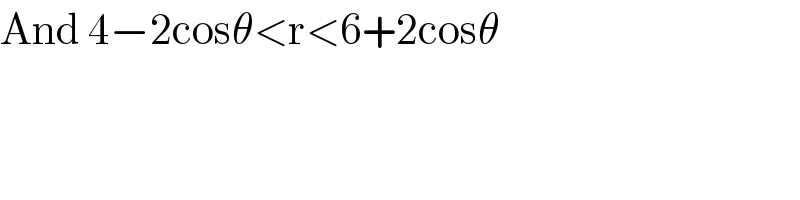
And 4−2cosθ<r<6+2cosθ

Commented bybemath last updated on 09/Jul/20

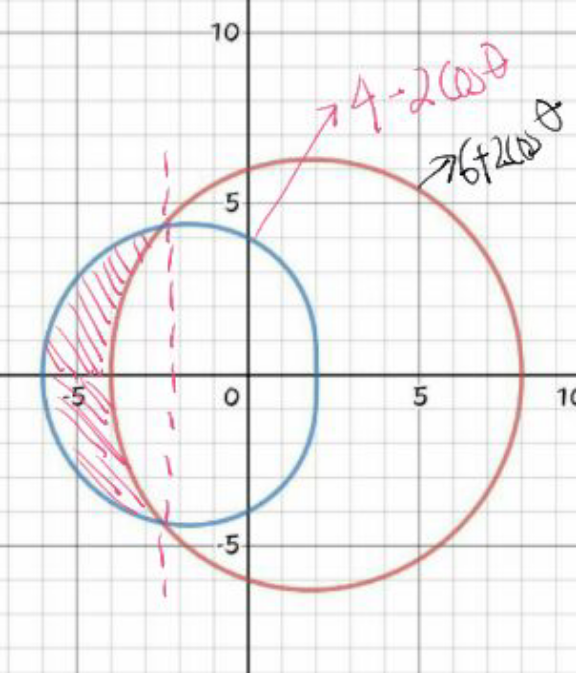
Commented by1549442205 last updated on 09/Jul/20

If the figure is bounded by { ((r=4−2cosθ)),((r=6)) :} then S=∫_0 ^π [6^2 −(4−2cosθ)^2 ]dθ =∫_0 ^π (20+16cosθ−4cos^2 θ)dθ =(20θ+16sinθ)∣_0 ^π −2∫_0 ^π (1+cos2θ)dθ =20𝛑−(2𝛉+sin2𝛉)∣_0 ^𝛑 =18𝛑 If the figure is bounded { ((r=4−2cosθ)),((r=6+2cosθ)) :}then S=∫_0 ^((2π)/3) [(6+2cosθ)^2 −(4−2cosθ)^2 ]dθ =∫_0 ^((2π)/3) (20+40cosθdθ=(20θ+40sinθ)∣_0 ^((2π)/3) =20×((2𝛑)/3)+40×((√3)/2)=((40𝛑)/3)−20(√(3 )) ≈76.53

Commented by1549442205 last updated on 09/Jul/20

Answered by Ar Brandon last updated on 09/Jul/20

Area , A=∫_((2π)/3) ^((4π)/3) ∫_(4−2cosθ) ^(6+2cosθ) rdrdθ=∫_((2π)/3) ^((4π)/3) [(r^2 /2)]_(4−2cosθ) ^(6+2cosθ) dθ ⇒A=(1/2)∫_((2π)/3) ^((4π)/3) {(6+2cosθ)^2 −(4−2cosθ)^2 }dθ =(1/2)∫_((2π)/3) ^((4π)/3) {(36+24cosθ+4cos^2 θ)−(16−16cosθ+4cos^2 θ)}dθ =(1/2)∫_((2π)/3) ^((4π)/3) (20+40cosθ)dθ=[((20θ+40sinθ)/2)]_((2π)/3) ^((4π)/3) =(1/2)[20×((4π)/3)−40×((√3)/2)−20×((2π)/3)+40×((√3)/2)] =((20)/3)π square units

Answered by bemath last updated on 09/Jul/20