Question and Answers Forum

All Questions      Topic List

Trigonometry Questions

Previous in All Question      Next in All Question      

Previous in Trigonometry      Next in Trigonometry      

Question Number 102390 by Dwaipayan Shikari last updated on 08/Jul/20

asinθ+bcosθ=c acosecθ+bsecθ=c prove that sin2θ=((2ab)/(c^2 −a^2 −b^2 ))

$${asin}\theta+{bcos}\theta={c} \\ $$$${acosec}\theta+{bsec}\theta={c} \\ $$$$ \\ $$$${prove}\:{that}\:\:\:\:{sin}\mathrm{2}\theta=\frac{\mathrm{2}{ab}}{{c}^{\mathrm{2}} −{a}^{\mathrm{2}} −{b}^{\mathrm{2}} } \\ $$

Commented by PRITHWISH SEN 2 last updated on 08/Jul/20

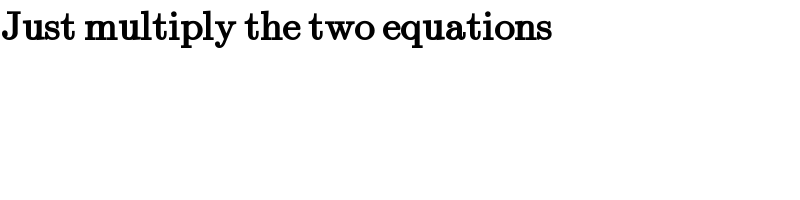
Just multiply the two equations

$$\boldsymbol{\mathrm{Just}}\:\boldsymbol{\mathrm{multiply}}\:\boldsymbol{\mathrm{the}}\:\boldsymbol{\mathrm{two}}\:\boldsymbol{\mathrm{equations}}\: \\ $$

Commented by bobhans last updated on 09/Jul/20

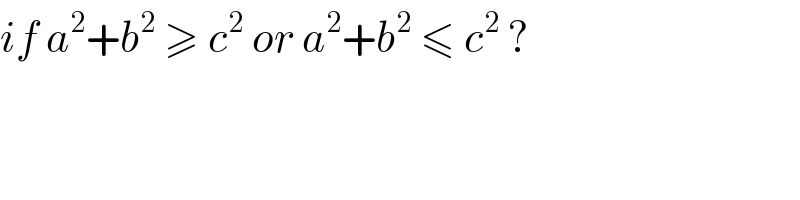
if a^2 +b^2 ≥ c^2 or a^2 +b^2 ≤ c^2 ?

$${if}\:{a}^{\mathrm{2}} +{b}^{\mathrm{2}} \:\geqslant\:{c}^{\mathrm{2}} \:{or}\:{a}^{\mathrm{2}} +{b}^{\mathrm{2}} \:\leqslant\:{c}^{\mathrm{2}} \:? \\ $$

Commented by bemath last updated on 09/Jul/20

(2)(a/(sin θ))+(b/(cos θ)) = c ((acos θ+bsin θ)/((1/2)sin 2θ)) = c ⇒acos θ+bsin θ=(1/2)c sin 2θ (1)×(2) (asin θ+bcos θ)(acos θ+bsin θ)=(1/2)c^2 sin 2θ (1/2)a^2 sin 2θ+absin^2 θ+abcos^2 θ+(1/2)b^2 sin 2θ=(1/2)c^2 sin 2θ {(1/2)a^2 +(1/2)b^2 }sin 2θ+ab=(1/2)c^2 sin 2θ ab = {(1/2)c^2 −(1/2)a^2 −(1/2)b^2 } sin 2θ sin 2θ = ((2ab)/(c^2 −a^2 −b^2 ))

$$\left(\mathrm{2}\right)\frac{{a}}{\mathrm{sin}\:\theta}+\frac{{b}}{\mathrm{cos}\:\theta}\:=\:{c}\: \\ $$$$\frac{{a}\mathrm{cos}\:\theta+{b}\mathrm{sin}\:\theta}{\frac{\mathrm{1}}{\mathrm{2}}\mathrm{sin}\:\mathrm{2}\theta}\:=\:{c}\:\Rightarrow{a}\mathrm{cos}\:\theta+{b}\mathrm{sin}\:\theta=\frac{\mathrm{1}}{\mathrm{2}}{c}\:\mathrm{sin}\:\mathrm{2}\theta \\ $$$$\left(\mathrm{1}\right)×\left(\mathrm{2}\right)\: \\ $$$$\left({a}\mathrm{sin}\:\theta+{b}\mathrm{cos}\:\theta\right)\left({a}\mathrm{cos}\:\theta+{b}\mathrm{sin}\:\theta\right)=\frac{\mathrm{1}}{\mathrm{2}}{c}^{\mathrm{2}} \:\mathrm{sin}\:\mathrm{2}\theta \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}{a}^{\mathrm{2}} \mathrm{sin}\:\mathrm{2}\theta+{ab}\mathrm{sin}\:^{\mathrm{2}} \theta+{ab}\mathrm{cos}\:^{\mathrm{2}} \theta+\frac{\mathrm{1}}{\mathrm{2}}{b}^{\mathrm{2}} \mathrm{sin}\:\mathrm{2}\theta=\frac{\mathrm{1}}{\mathrm{2}}{c}^{\mathrm{2}} \:\mathrm{sin}\:\mathrm{2}\theta \\ $$$$\left\{\frac{\mathrm{1}}{\mathrm{2}}{a}^{\mathrm{2}} +\frac{\mathrm{1}}{\mathrm{2}}{b}^{\mathrm{2}} \right\}\mathrm{sin}\:\mathrm{2}\theta+{ab}=\frac{\mathrm{1}}{\mathrm{2}}{c}^{\mathrm{2}} \:\mathrm{sin}\:\mathrm{2}\theta \\ $$$${ab}\:=\:\left\{\frac{\mathrm{1}}{\mathrm{2}}{c}^{\mathrm{2}} −\frac{\mathrm{1}}{\mathrm{2}}{a}^{\mathrm{2}} −\frac{\mathrm{1}}{\mathrm{2}}{b}^{\mathrm{2}} \right\}\:\mathrm{sin}\:\mathrm{2}\theta \\ $$$$\mathrm{sin}\:\mathrm{2}\theta\:=\:\frac{\mathrm{2}{ab}}{{c}^{\mathrm{2}} −{a}^{\mathrm{2}} −{b}^{\mathrm{2}} } \\ $$

Commented by 1549442205 last updated on 09/Jul/20

$$ \\ $$

Answered by Dwaipayan Shikari last updated on 08/Jul/20

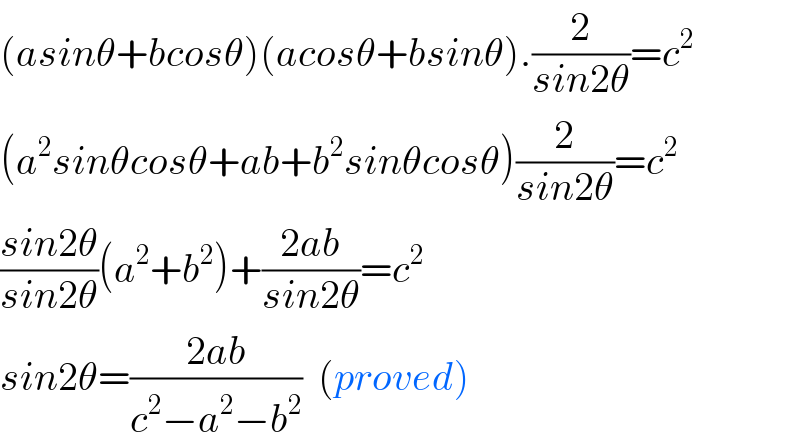
(asinθ+bcosθ)(acosθ+bsinθ).(2/(sin2θ))=c^2 (a^2 sinθcosθ+ab+b^2 sinθcosθ)(2/(sin2θ))=c^2 ((sin2θ)/(sin2θ))(a^2 +b^2 )+((2ab)/(sin2θ))=c^2 sin2θ=((2ab)/(c^2 −a^2 −b^2 )) (proved)

$$\left({asin}\theta+{bcos}\theta\right)\left({acos}\theta+{bsin}\theta\right).\frac{\mathrm{2}}{{sin}\mathrm{2}\theta}={c}^{\mathrm{2}} \\ $$$$\left({a}^{\mathrm{2}} {sin}\theta{cos}\theta+{ab}+{b}^{\mathrm{2}} {sin}\theta{cos}\theta\right)\frac{\mathrm{2}}{{sin}\mathrm{2}\theta}={c}^{\mathrm{2}} \\ $$$$\frac{{sin}\mathrm{2}\theta}{{sin}\mathrm{2}\theta}\left({a}^{\mathrm{2}} +{b}^{\mathrm{2}} \right)+\frac{\mathrm{2}{ab}}{{sin}\mathrm{2}\theta}={c}^{\mathrm{2}} \\ $$$${sin}\mathrm{2}\theta=\frac{\mathrm{2}{ab}}{{c}^{\mathrm{2}} −{a}^{\mathrm{2}} −{b}^{\mathrm{2}} }\:\:\left({proved}\right) \\ $$

Commented by bobhans last updated on 09/Jul/20

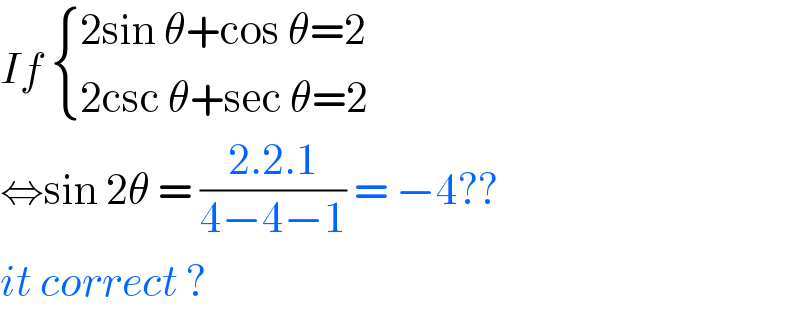
If { ((2sin θ+cos θ=2)),((2csc θ+sec θ=2)) :} ⇔sin 2θ = ((2.2.1)/(4−4−1)) = −4?? it correct ?

$${If}\:\begin{cases}{\mathrm{2sin}\:\theta+\mathrm{cos}\:\theta=\mathrm{2}}\\{\mathrm{2csc}\:\theta+\mathrm{sec}\:\theta=\mathrm{2}}\end{cases} \\ $$$$\Leftrightarrow\mathrm{sin}\:\mathrm{2}\theta\:=\:\frac{\mathrm{2}.\mathrm{2}.\mathrm{1}}{\mathrm{4}−\mathrm{4}−\mathrm{1}}\:=\:−\mathrm{4}??\: \\ $$$${it}\:{correct}\:?\: \\ $$

Commented by 1549442205 last updated on 09/Jul/20

but the your system has no roots ! the first eqs implies that sin2θ=((24)/(25))!

$$\mathrm{but}\:\mathrm{the}\:\mathrm{your}\:\mathrm{system}\:\mathrm{has}\:\mathrm{no}\:\mathrm{roots}\:! \\ $$$$\mathrm{the}\:\mathrm{first}\:\mathrm{eqs}\:\mathrm{implies}\:\mathrm{that}\:\mathrm{sin2}\theta=\frac{\mathrm{24}}{\mathrm{25}}! \\ $$

Commented by PRITHWISH SEN 2 last updated on 09/Jul/20

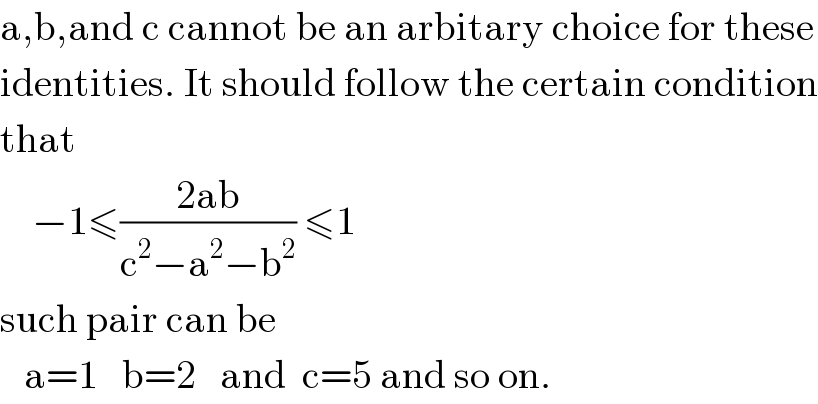
a,b,and c cannot be an arbitary choice for these identities. It should follow the certain condition that −1≤((2ab)/(c^2 −a^2 −b^2 )) ≤1 such pair can be a=1 b=2 and c=5 and so on.

$$\mathrm{a},\mathrm{b},\mathrm{and}\:\mathrm{c}\:\mathrm{cannot}\:\mathrm{be}\:\mathrm{an}\:\mathrm{arbitary}\:\mathrm{choice}\:\mathrm{for}\:\mathrm{these} \\ $$$$\mathrm{identities}.\:\mathrm{It}\:\mathrm{should}\:\mathrm{follow}\:\mathrm{the}\:\mathrm{certain}\:\mathrm{condition} \\ $$$$\mathrm{that} \\ $$$$\:\:\:\:−\mathrm{1}\leqslant\frac{\mathrm{2ab}}{\mathrm{c}^{\mathrm{2}} −\mathrm{a}^{\mathrm{2}} −\mathrm{b}^{\mathrm{2}} }\:\leqslant\mathrm{1} \\ $$$$\mathrm{such}\:\mathrm{pair}\:\mathrm{can}\:\mathrm{be} \\ $$$$\:\:\:\mathrm{a}=\mathrm{1}\:\:\:\mathrm{b}=\mathrm{2}\:\:\:\mathrm{and}\:\:\mathrm{c}=\mathrm{5}\:\mathrm{and}\:\mathrm{so}\:\mathrm{on}. \\ $$

Commented by bemath last updated on 09/Jul/20

it does meant c^2 ≥ a^2 +b^2

$${it}\:{does}\:{meant}\:{c}^{\mathrm{2}} \:\geqslant\:{a}^{\mathrm{2}} +{b}^{\mathrm{2}} \\ $$

Answered by 1549442205 last updated on 09/Jul/20

(1)⇔(a/(√(a^2 +b^2 )))sinθ+(b/(√(a^2 +b^2 )))cosθ=(c/(√(a^2 +b^2 ))) ⇔sin(ϕ+θ)=sin[sin^(−1) ((c/(√(a^2 +b^2 ))))](where ϕ=arccos(a/(√(a^2 +b^2 )))) (with the condition a^2 +b^2 ≥c^2 ) ⇒ϕ+θ=sin^(−1) ((c/(√(a^2 +b^2 ))))+2kπ ⇒θ=sin^(−1) ((c/(√(a^2 +b^2 ))))+2kπ−ϕ ⇒sinθ=sin(sin^(−1) ((c/(√(a^2 +b^2 ))))−ϕ) =(c/(√(a^2 +b^2 )))cosϕ−((√(a^2 +b^2 −c^2 ))/(√(a^2 +b^2 )))sinϕ =(c/(√(a^2 +b^2 ))).(a/(√(a^2 +b^2 )))−((√(a^2 +b^2 −c^2 ))/(√(a^2 +b^2 ))).(b/(√(a^2 +b^2 ))) =((ac−b(√(a^2 +b^2 −c^2 )))/(a^2 +b^2 )) ⇒cosθ=(1/(a^2 +b^2 ))(√((a^2 +b^2 )^2 −(ac−b(√(a^2 +b^2 −c^2 )^2 )))) ⇒sin2θ=2sinθcosθ=2(((ac−b(√(a^2 +b^2 −c^2 )))/(a^2 +b^2 )))((1/(a^2 +b^2 ))(√((a^2 +b^2 )^2 −(ac−b(√(a^2 +b^2 −c^2 )^2 )))) )=f(a,b,c)

$$\left(\mathrm{1}\right)\Leftrightarrow\frac{\mathrm{a}}{\sqrt{\mathrm{a}^{\mathrm{2}} +\mathrm{b}^{\mathrm{2}} }}\mathrm{sin}\theta+\frac{\mathrm{b}}{\sqrt{\mathrm{a}^{\mathrm{2}} +\mathrm{b}^{\mathrm{2}} }}\mathrm{cos}\theta=\frac{\mathrm{c}}{\sqrt{\mathrm{a}^{\mathrm{2}} +\mathrm{b}^{\mathrm{2}} }} \\ $$$$\Leftrightarrow\mathrm{sin}\left(\varphi+\theta\right)=\mathrm{sin}\left[\mathrm{sin}^{−\mathrm{1}} \left(\frac{\mathrm{c}}{\sqrt{\mathrm{a}^{\mathrm{2}} +\mathrm{b}^{\mathrm{2}} }}\right)\right]\left(\mathrm{where}\:\varphi=\mathrm{arccos}\frac{\mathrm{a}}{\sqrt{\mathrm{a}^{\mathrm{2}} +\mathrm{b}^{\mathrm{2}} }}\right) \\ $$$$\left(\mathrm{with}\:\mathrm{the}\:\mathrm{condition}\:\mathrm{a}^{\mathrm{2}} +\mathrm{b}^{\mathrm{2}} \geqslant\mathrm{c}^{\mathrm{2}} \right) \\ $$$$\Rightarrow\varphi+\theta=\mathrm{sin}^{−\mathrm{1}} \left(\frac{\mathrm{c}}{\sqrt{\mathrm{a}^{\mathrm{2}} +\mathrm{b}^{\mathrm{2}} }}\right)+\mathrm{2k}\pi \\ $$$$\Rightarrow\theta=\mathrm{sin}^{−\mathrm{1}} \left(\frac{\mathrm{c}}{\sqrt{\mathrm{a}^{\mathrm{2}} +\mathrm{b}^{\mathrm{2}} }}\right)+\mathrm{2k}\pi−\varphi \\ $$$$\Rightarrow\mathrm{sin}\theta=\mathrm{sin}\left(\mathrm{sin}^{−\mathrm{1}} \left(\frac{\mathrm{c}}{\sqrt{\mathrm{a}^{\mathrm{2}} +\mathrm{b}^{\mathrm{2}} }}\right)−\varphi\right) \\ $$$$=\frac{\mathrm{c}}{\sqrt{\mathrm{a}^{\mathrm{2}} +\mathrm{b}^{\mathrm{2}} }}\mathrm{cos}\varphi−\frac{\sqrt{\mathrm{a}^{\mathrm{2}} +\mathrm{b}^{\mathrm{2}} −\mathrm{c}^{\mathrm{2}} }}{\sqrt{\mathrm{a}^{\mathrm{2}} +\mathrm{b}^{\mathrm{2}} }}\mathrm{sin}\varphi \\ $$$$=\frac{\mathrm{c}}{\sqrt{\mathrm{a}^{\mathrm{2}} +\mathrm{b}^{\mathrm{2}} }}.\frac{\mathrm{a}}{\sqrt{\mathrm{a}^{\mathrm{2}} +\mathrm{b}^{\mathrm{2}} }}−\frac{\sqrt{\mathrm{a}^{\mathrm{2}} +\mathrm{b}^{\mathrm{2}} −\mathrm{c}^{\mathrm{2}} }}{\sqrt{\mathrm{a}^{\mathrm{2}} +\mathrm{b}^{\mathrm{2}} }}.\frac{\mathrm{b}}{\sqrt{\mathrm{a}^{\mathrm{2}} +\mathrm{b}^{\mathrm{2}} }} \\ $$$$=\frac{\mathrm{ac}−\mathrm{b}\sqrt{\mathrm{a}^{\mathrm{2}} +\mathrm{b}^{\mathrm{2}} −\mathrm{c}^{\mathrm{2}} }}{\mathrm{a}^{\mathrm{2}} +\mathrm{b}^{\mathrm{2}} } \\ $$$$\Rightarrow\mathrm{cos}\theta=\frac{\mathrm{1}}{\mathrm{a}^{\mathrm{2}} +\mathrm{b}^{\mathrm{2}} }\sqrt{\left(\mathrm{a}^{\mathrm{2}} +\mathrm{b}^{\mathrm{2}} \right)^{\mathrm{2}} −\left(\mathrm{ac}−\mathrm{b}\sqrt{\left.\mathrm{a}^{\mathrm{2}} +\mathrm{b}^{\mathrm{2}} −\mathrm{c}^{\mathrm{2}} \right)^{\mathrm{2}} }\right.} \\ $$$$\Rightarrow\mathrm{sin2}\theta=\mathrm{2sin}\theta\mathrm{cos}\theta=\mathrm{2}\left(\frac{\mathrm{ac}−\mathrm{b}\sqrt{\mathrm{a}^{\mathrm{2}} +\mathrm{b}^{\mathrm{2}} −\mathrm{c}^{\mathrm{2}} }}{\mathrm{a}^{\mathrm{2}} +\mathrm{b}^{\mathrm{2}} }\right)\left(\frac{\mathrm{1}}{\mathrm{a}^{\mathrm{2}} +\mathrm{b}^{\mathrm{2}} }\sqrt{\left(\mathrm{a}^{\mathrm{2}} +\mathrm{b}^{\mathrm{2}} \right)^{\mathrm{2}} −\left(\mathrm{ac}−\mathrm{b}\sqrt{\left.\mathrm{a}^{\mathrm{2}} +\mathrm{b}^{\mathrm{2}} −\mathrm{c}^{\mathrm{2}} \right)^{\mathrm{2}} }\right.}\:\right)=\mathrm{f}\left(\mathrm{a},\mathrm{b},\mathrm{c}\right) \\ $$$$ \\ $$$$ \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com