
Question Number 102416 by mathmax by abdo last updated on 09/Jul/20
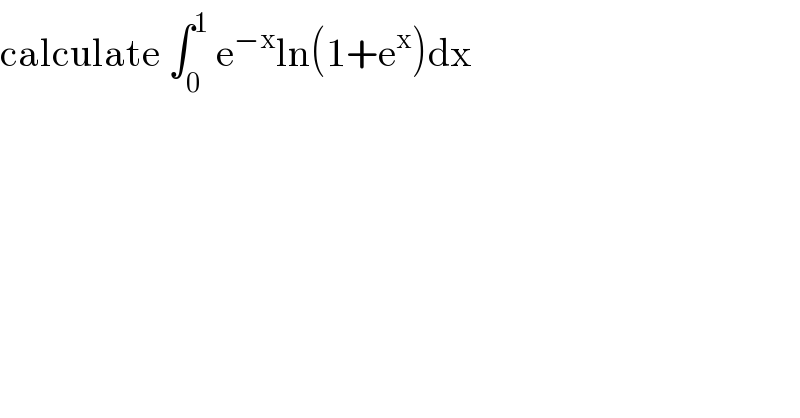
$$\mathrm{calculate}\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\mathrm{e}^{−\mathrm{x}} \mathrm{ln}\left(\mathrm{1}+\mathrm{e}^{\mathrm{x}} \right)\mathrm{dx} \\ $$
Answered by OlafThorendsen last updated on 09/Jul/20
![I = ∫_0 ^1 e^(−x) ln(1+e^x )dx u = e^x ⇒ dx = (du/u) I = ∫_1 ^e (1/u)ln(1+u)(du/u) I = ∫_1 ^e (1/u^2 )ln(1+u)du I = [−(1/u)ln(1+u)]_1 ^e −∫_1 ^e (−(1/u))(1/(1+u))du I = ln2−(1/e)ln(1+e)+∫_1 ^e ((1/u)−(1/(1+u)))du I = ln2−(1/e)ln(1+e)+[ln(u/(1+u))]_1 ^e I = ln2−(1/e)ln(1+e)+ln(e/(1+e))−ln(1/2) I = 2ln2+1−(1+(1/e))ln(1+e)](Q102430.png)
$$\mathrm{I}\:=\:\int_{\mathrm{0}} ^{\mathrm{1}} {e}^{−{x}} \mathrm{ln}\left(\mathrm{1}+{e}^{{x}} \right){dx} \\ $$$${u}\:=\:{e}^{{x}} \:\Rightarrow\:{dx}\:=\:\frac{{du}}{{u}} \\ $$$$\mathrm{I}\:=\:\int_{\mathrm{1}} ^{{e}} \frac{\mathrm{1}}{{u}}\mathrm{ln}\left(\mathrm{1}+{u}\right)\frac{{du}}{{u}} \\ $$$$\mathrm{I}\:=\:\int_{\mathrm{1}} ^{{e}} \frac{\mathrm{1}}{{u}^{\mathrm{2}} }\mathrm{ln}\left(\mathrm{1}+{u}\right){du} \\ $$$$\mathrm{I}\:=\:\left[−\frac{\mathrm{1}}{{u}}\mathrm{ln}\left(\mathrm{1}+{u}\right)\right]_{\mathrm{1}} ^{{e}} −\int_{\mathrm{1}} ^{{e}} \left(−\frac{\mathrm{1}}{{u}}\right)\frac{\mathrm{1}}{\mathrm{1}+{u}}{du} \\ $$$$\mathrm{I}\:=\:\mathrm{ln2}−\frac{\mathrm{1}}{{e}}\mathrm{ln}\left(\mathrm{1}+{e}\right)+\int_{\mathrm{1}} ^{{e}} \left(\frac{\mathrm{1}}{{u}}−\frac{\mathrm{1}}{\mathrm{1}+{u}}\right){du} \\ $$$$\mathrm{I}\:=\:\mathrm{ln2}−\frac{\mathrm{1}}{{e}}\mathrm{ln}\left(\mathrm{1}+{e}\right)+\left[\mathrm{ln}\frac{{u}}{\mathrm{1}+{u}}\right]_{\mathrm{1}} ^{{e}} \\ $$$$\mathrm{I}\:=\:\mathrm{ln2}−\frac{\mathrm{1}}{{e}}\mathrm{ln}\left(\mathrm{1}+{e}\right)+\mathrm{ln}\frac{{e}}{\mathrm{1}+{e}}−\mathrm{ln}\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\mathrm{I}\:=\:\mathrm{2ln2}+\mathrm{1}−\left(\mathrm{1}+\frac{\mathrm{1}}{{e}}\right)\mathrm{ln}\left(\mathrm{1}+{e}\right) \\ $$$$ \\ $$$$ \\ $$
Answered by mathmax by abdo last updated on 10/Jul/20
![A =∫_0 ^1 e^(−x) ln(1+e^x )dx by parts u^′ =e^(−x ) and v =ln(1+e^x ) A = [−e^(−x) ln(1+e^x )]_0 ^1 +∫_0 ^(1 ) e^(−x) ×(e^x /(1+e^x ))dx =ln(2)−e^(−1) ln( 1+e) +∫_0 ^1 (dx/(1+e^x )) (→e^x =t) =ln(2)−e^(−1) ln(1+e) +∫_1 ^e (dt/(t(1+t))) we have ∫_1 ^e (dt/(t(t+1))) =∫_1 ^e ((1/t)−(1/(t+1)))dt =[ln∣(t/(t+1))∣]_1 ^e =ln((e/(e+1))) −ln((1/2)) =1−ln(e+1)+ln(2) ⇒ A =ln(2)−e^(−1) ln(1+e) +1−ln(e+1)+ln(2) =2ln(2)−e^(−1) ln(e+1)−ln(e+1) +1](Q102697.png)
$$\mathrm{A}\:=\int_{\mathrm{0}} ^{\mathrm{1}} \:\mathrm{e}^{−\mathrm{x}} \mathrm{ln}\left(\mathrm{1}+\mathrm{e}^{\mathrm{x}} \right)\mathrm{dx}\:\:\mathrm{by}\:\mathrm{parts}\:\mathrm{u}^{'} \:=\mathrm{e}^{−\mathrm{x}\:} \:\mathrm{and}\:\mathrm{v}\:=\mathrm{ln}\left(\mathrm{1}+\mathrm{e}^{\mathrm{x}} \right) \\ $$$$\mathrm{A}\:=\:\left[−\mathrm{e}^{−\mathrm{x}} \mathrm{ln}\left(\mathrm{1}+\mathrm{e}^{\mathrm{x}} \right)\right]_{\mathrm{0}} ^{\mathrm{1}} \:+\int_{\mathrm{0}} ^{\mathrm{1}\:} \:\:\mathrm{e}^{−\mathrm{x}} \:×\frac{\mathrm{e}^{\mathrm{x}} }{\mathrm{1}+\mathrm{e}^{\mathrm{x}} }\mathrm{dx}\: \\ $$$$=\mathrm{ln}\left(\mathrm{2}\right)−\mathrm{e}^{−\mathrm{1}} \mathrm{ln}\left(\:\mathrm{1}+\mathrm{e}\right)\:+\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\mathrm{dx}}{\mathrm{1}+\mathrm{e}^{\mathrm{x}} }\:\:\left(\rightarrow\mathrm{e}^{\mathrm{x}} \:=\mathrm{t}\right) \\ $$$$=\mathrm{ln}\left(\mathrm{2}\right)−\mathrm{e}^{−\mathrm{1}} \mathrm{ln}\left(\mathrm{1}+\mathrm{e}\right)\:+\int_{\mathrm{1}} ^{\mathrm{e}} \:\:\frac{\mathrm{dt}}{\mathrm{t}\left(\mathrm{1}+\mathrm{t}\right)} \\ $$$$\mathrm{we}\:\mathrm{have}\:\int_{\mathrm{1}} ^{\mathrm{e}} \:\frac{\mathrm{dt}}{\mathrm{t}\left(\mathrm{t}+\mathrm{1}\right)}\:=\int_{\mathrm{1}} ^{\mathrm{e}} \left(\frac{\mathrm{1}}{\mathrm{t}}−\frac{\mathrm{1}}{\mathrm{t}+\mathrm{1}}\right)\mathrm{dt}\:=\left[\mathrm{ln}\mid\frac{\mathrm{t}}{\mathrm{t}+\mathrm{1}}\mid\right]_{\mathrm{1}} ^{\mathrm{e}} \\ $$$$=\mathrm{ln}\left(\frac{\mathrm{e}}{\mathrm{e}+\mathrm{1}}\right)\:−\mathrm{ln}\left(\frac{\mathrm{1}}{\mathrm{2}}\right)\:=\mathrm{1}−\mathrm{ln}\left(\mathrm{e}+\mathrm{1}\right)+\mathrm{ln}\left(\mathrm{2}\right)\:\Rightarrow \\ $$$$\mathrm{A}\:=\mathrm{ln}\left(\mathrm{2}\right)−\mathrm{e}^{−\mathrm{1}} \mathrm{ln}\left(\mathrm{1}+\mathrm{e}\right)\:+\mathrm{1}−\mathrm{ln}\left(\mathrm{e}+\mathrm{1}\right)+\mathrm{ln}\left(\mathrm{2}\right) \\ $$$$=\mathrm{2ln}\left(\mathrm{2}\right)−\mathrm{e}^{−\mathrm{1}} \mathrm{ln}\left(\mathrm{e}+\mathrm{1}\right)−\mathrm{ln}\left(\mathrm{e}+\mathrm{1}\right)\:+\mathrm{1} \\ $$
