Question and Answers Forum

All Questions      Topic List

None Questions

Previous in All Question      Next in All Question      

Previous in None      Next in None      

Question Number 102450 by naka3546 last updated on 09/Jul/20

Commented by naka3546 last updated on 09/Jul/20

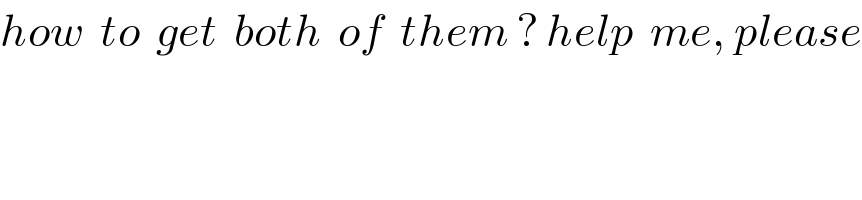
$$howtogetbothofthem?helpme,please$$

Commented by bemath last updated on 09/Jul/20

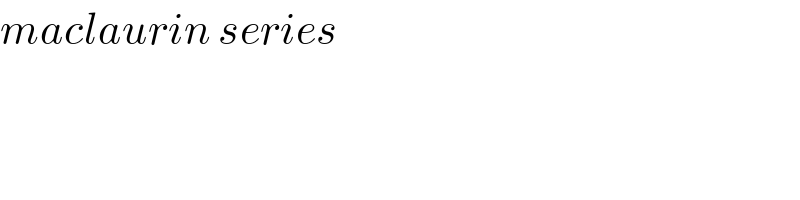
$$maclaurinseries$$

Answered by Rio Michael last updated on 09/Jul/20

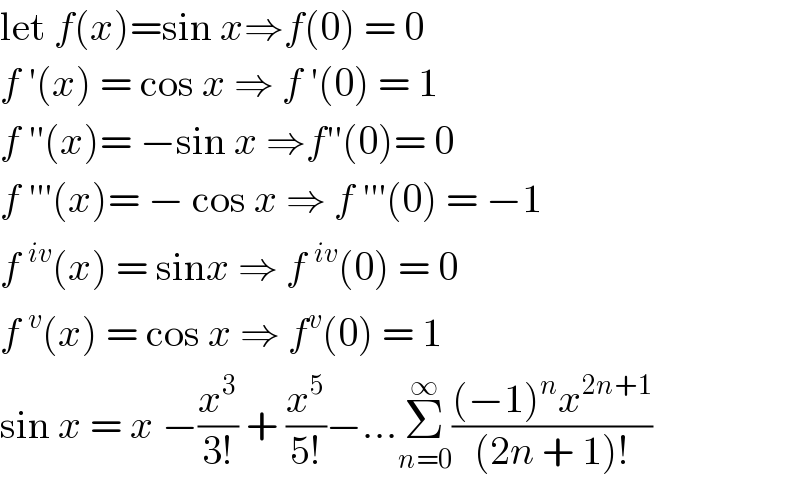
$$\mathrm{let}f\left(x\right)=\sin x\Rightarrow f\left(0\right)=0$$$$f{}^{\prime }\left(x\right)=\cos x\Rightarrow f{}^{\prime }\left(0\right)=1$$$$f{}^{″}\left(x\right)=-\sin x\Rightarrow f^{″}\left(0\right)=0$$$$f{}^{‴}\left(x\right)=-\cos x\Rightarrow f{}^{‴}\left(0\right)=-1$$$$f{}^{iv}\left(x\right)=\sin x\Rightarrow f{}^{iv}\left(0\right)=0$$$$f{}^v\left(x\right)=\cos x\Rightarrow f^v\left(0\right)=1$$$$\sin x=x-\frac{x^3}{3!}+\frac{x^5}{5!}-...\underset{n=0}{\sum ^{\mathrm{\infty }}}\frac{{(-1)}^n{x}^{2n+1}}{(2n+1)!}$$

Answered by Dwaipayan Shikari last updated on 09/Jul/20

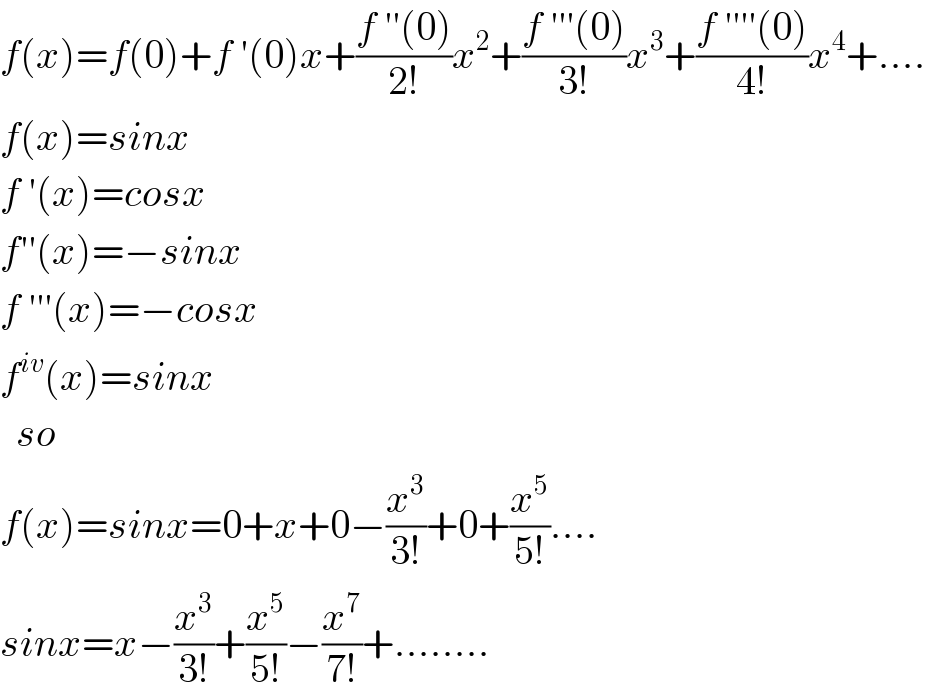
$$f\left(x\right)=f\left(0\right)+f{}^{\prime }\left(0\right)x+\frac{f{}^{″}\left(0\right)}{2!}{x}^2+\frac{f{}^{‴}\left(0\right)}{3!}{x}^3+\frac{f{}^{⁗}\left(0\right)}{4!}{x}^4+....$$$$f\left(x\right)=sinx$$$$f{}^{\prime }\left(x\right)=cosx$$$$f^{″}\left(x\right)=-sinx$$$$f{}^{‴}\left(x\right)=-cosx$$$$f^{iv}\left(x\right)=sinx$$$$so$$$$f\left(x\right)=sinx=0+x+0-\frac{x^3}{3!}+0+\frac{x^5}{5!}....$$$$sinx=x-\frac{x^3}{3!}+\frac{x^5}{5!}-\frac{x^7}{7!}+........$$

Answered by PRITHWISH SEN 2 last updated on 09/Jul/20

$$\cos \mathrm{x}+\mathrm{isin}\mathrm{x}={\mathrm{e}}^{\mathrm{ix}}=1+\mathrm{ix}-\frac{{\mathrm{x}}^2}{2!}-\mathrm{i}\frac{{\mathrm{x}}^3}{3!}+\frac{{\mathrm{x}}^4}{4!}+\mathrm{i}\frac{{\mathrm{x}}^5}{5!}-\frac{{\mathrm{x}}^6}{6!}-\mathrm{i}\frac{{\mathrm{x}}^7}{7!}+...$$$$\mathbf{Now}\mathbf{compairing}\mathbf{the}\mathbf{real}\mathbf{and}\mathbf{imaginary}\mathbf{part}$$$$\cos \mathbf{x}=1-\frac{{\mathbf{x}}^2}{2!}+\frac{{\mathbf{x}}^4}{4!}-\frac{{\mathbf{x}}^6}{6!}+.....$$$$\mathbf{and}$$$$\sin \mathbf{x}=\mathbf{x}-\frac{{\mathbf{x}}^3}{3!}+\frac{{\mathbf{x}}^5}{5!}-\frac{{\mathbf{x}}^7}{7!}+......$$$$\mathbf{please}\mathbf{check}\mathbf{your}\mathbf{question}.$$$$\mathrm{the}1\mathrm{st}\mathrm{one}\mathrm{also}\mathrm{has}\mathrm{a}\mathrm{trignometrical}\mathrm{approach}$$$$\mathrm{but}\mathrm{it}\mathrm{is}\mathrm{too}\mathrm{lengthy}.$$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com