Question and Answers Forum

All Questions      Topic List

Integration Questions

Previous in All Question      Next in All Question      

Previous in Integration      Next in Integration      

Question Number 102462 by Ar Brandon last updated on 09/Jul/20

Calculate ; J=∫(dx/(x(x^2 +x−1)^2 )) K=∫((x^3 +x−1)/((x^2 +2)^2 ))dx L=∫(dx/(x+(√(x^2 +1))))

$$\mathrm{Calculate}\:; \\ $$$$\mathrm{J}=\int\frac{\mathrm{dx}}{\mathrm{x}\left(\mathrm{x}^{\mathrm{2}} +\mathrm{x}−\mathrm{1}\right)^{\mathrm{2}} } \\ $$$$\mathrm{K}=\int\frac{\mathrm{x}^{\mathrm{3}} +\mathrm{x}−\mathrm{1}}{\left(\mathrm{x}^{\mathrm{2}} +\mathrm{2}\right)^{\mathrm{2}} }\mathrm{dx} \\ $$$$\mathrm{L}=\int\frac{\mathrm{dx}}{\mathrm{x}+\sqrt{\mathrm{x}^{\mathrm{2}} +\mathrm{1}}} \\ $$

Answered by bemath last updated on 09/Jul/20

L=((x−(√(x^2 +1)))/(x^2 −(x^2 +1)))= (((√(x^2 +1))−x)/1) ∫ {(√(x^2 +1))−x} dx = I_1 = ∫(√(x^2 +1)) dx x= tan p ⇒dx = sec^2 p dp I_1 = ∫sec^3 p dp = ((sin p)/(2cos^2 p))+(1/2)ln∣tan ((p/2)+(π/4))∣ I_2 = ∫x dx = (1/2)x^2 I=I_1 −I_2

$${L}=\frac{{x}−\sqrt{{x}^{\mathrm{2}} +\mathrm{1}}}{{x}^{\mathrm{2}} −\left({x}^{\mathrm{2}} +\mathrm{1}\right)}=\:\frac{\sqrt{{x}^{\mathrm{2}} +\mathrm{1}}−{x}}{\mathrm{1}} \\ $$$$\int\:\left\{\sqrt{{x}^{\mathrm{2}} +\mathrm{1}}−{x}\right\}\:{dx}\:= \\ $$$${I}_{\mathrm{1}} \:=\:\int\sqrt{{x}^{\mathrm{2}} +\mathrm{1}}\:{dx}\: \\ $$$${x}=\:\mathrm{tan}\:{p}\:\Rightarrow{dx}\:=\:\mathrm{sec}\:^{\mathrm{2}} {p}\:{dp} \\ $$$${I}_{\mathrm{1}} =\:\int\mathrm{sec}\:^{\mathrm{3}} {p}\:{dp}\:=\:\frac{\mathrm{sin}\:{p}}{\mathrm{2cos}\:^{\mathrm{2}} {p}}+\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ln}\mid\mathrm{tan}\:\left(\frac{{p}}{\mathrm{2}}+\frac{\pi}{\mathrm{4}}\right)\mid \\ $$$${I}_{\mathrm{2}} \:=\:\int{x}\:{dx}\:=\:\frac{\mathrm{1}}{\mathrm{2}}{x}^{\mathrm{2}} \: \\ $$$${I}={I}_{\mathrm{1}} −{I}_{\mathrm{2}} \\ $$

Answered by Dwaipayan Shikari last updated on 09/Jul/20

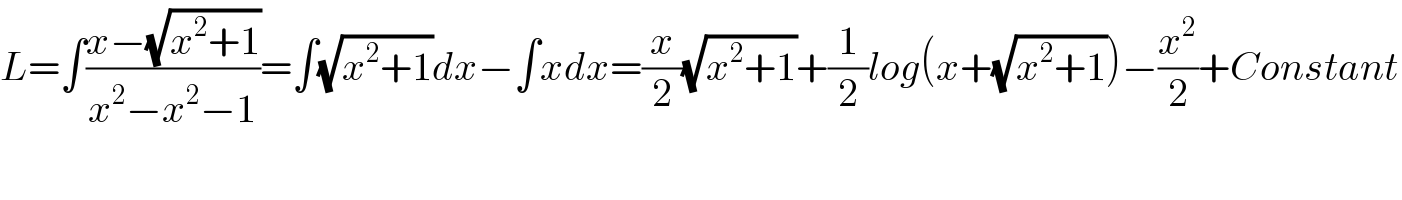
L=∫((x−(√(x^2 +1)))/(x^2 −x^2 −1))=∫(√(x^2 +1))dx−∫xdx=(x/2)(√(x^2 +1))+(1/2)log(x+(√(x^2 +1)))−(x^2 /2)+Constant

$${L}=\int\frac{{x}−\sqrt{{x}^{\mathrm{2}} +\mathrm{1}}}{{x}^{\mathrm{2}} −{x}^{\mathrm{2}} −\mathrm{1}}=\int\sqrt{{x}^{\mathrm{2}} +\mathrm{1}}{dx}−\int{xdx}=\frac{{x}}{\mathrm{2}}\sqrt{{x}^{\mathrm{2}} +\mathrm{1}}+\frac{\mathrm{1}}{\mathrm{2}}{log}\left({x}+\sqrt{{x}^{\mathrm{2}} +\mathrm{1}}\right)−\frac{{x}^{\mathrm{2}} }{\mathrm{2}}+{Constant} \\ $$

Answered by PRITHWISH SEN 2 last updated on 09/Jul/20

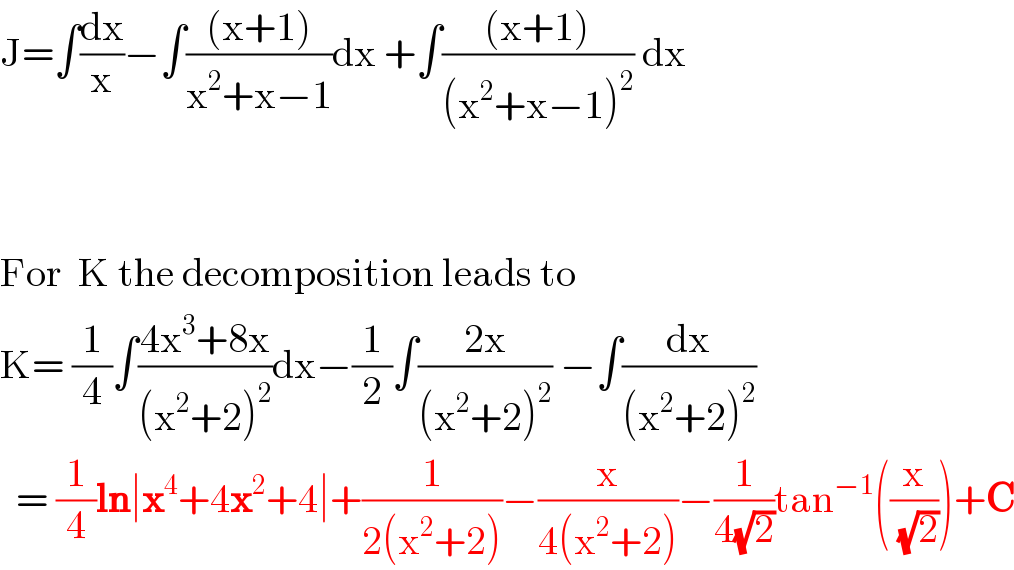
J=∫(dx/x)−∫(((x+1))/(x^2 +x−1))dx +∫(((x+1))/((x^2 +x−1)^2 )) dx For K the decomposition leads to K= (1/4)∫((4x^3 +8x)/((x^2 +2)^2 ))dx−(1/2)∫((2x)/((x^2 +2)^2 )) −∫(dx/((x^2 +2)^2 )) = (1/4)ln∣x^4 +4x^2 +4∣+(1/(2(x^2 +2)))−(x/(4(x^2 +2)))−(1/(4(√2)))tan^(−1) ((x/(√2)))+C

$$\mathrm{J}=\int\frac{\mathrm{dx}}{\mathrm{x}}−\int\frac{\left(\mathrm{x}+\mathrm{1}\right)}{\mathrm{x}^{\mathrm{2}} +\mathrm{x}−\mathrm{1}}\mathrm{dx}\:+\int\frac{\left(\mathrm{x}+\mathrm{1}\right)}{\left(\mathrm{x}^{\mathrm{2}} +\mathrm{x}−\mathrm{1}\right)^{\mathrm{2}} }\:\mathrm{dx} \\ $$$$ \\ $$$$ \\ $$$$\mathrm{For}\:\:\mathrm{K}\:\mathrm{the}\:\mathrm{decomposition}\:\mathrm{leads}\:\mathrm{to} \\ $$$$\mathrm{K}=\:\frac{\mathrm{1}}{\mathrm{4}}\int\frac{\mathrm{4x}^{\mathrm{3}} +\mathrm{8x}}{\left(\mathrm{x}^{\mathrm{2}} +\mathrm{2}\right)^{\mathrm{2}} }\mathrm{dx}−\frac{\mathrm{1}}{\mathrm{2}}\int\frac{\mathrm{2x}}{\left(\mathrm{x}^{\mathrm{2}} +\mathrm{2}\right)^{\mathrm{2}} }\:−\int\frac{\mathrm{dx}}{\left(\mathrm{x}^{\mathrm{2}} +\mathrm{2}\right)^{\mathrm{2}} } \\ $$$$\:\:=\:\frac{\mathrm{1}}{\mathrm{4}}\boldsymbol{\mathrm{ln}}\mid\boldsymbol{\mathrm{x}}^{\mathrm{4}} +\mathrm{4}\boldsymbol{\mathrm{x}}^{\mathrm{2}} +\mathrm{4}\mid+\frac{\mathrm{1}}{\mathrm{2}\left(\mathrm{x}^{\mathrm{2}} +\mathrm{2}\right)}−\frac{\mathrm{x}}{\mathrm{4}\left(\mathrm{x}^{\mathrm{2}} +\mathrm{2}\right)}−\frac{\mathrm{1}}{\mathrm{4}\sqrt{\mathrm{2}}}\mathrm{tan}^{−\mathrm{1}} \left(\frac{\mathrm{x}}{\sqrt{\mathrm{2}}}\right)+\boldsymbol{\mathrm{C}} \\ $$

Commented by Ar Brandon last updated on 09/Jul/20

Thanks for your time.��

Answered by 1549442205 last updated on 09/Jul/20

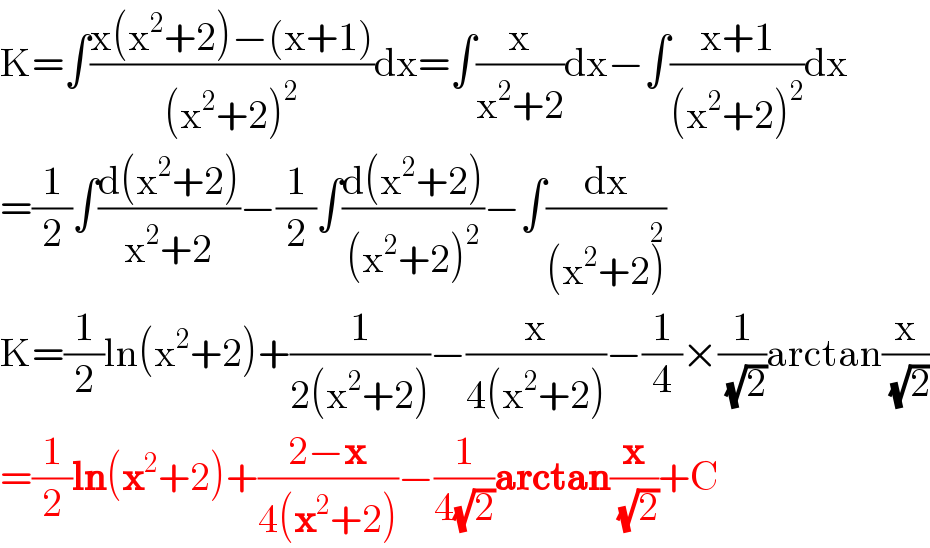
K=∫((x(x^2 +2)−(x+1))/((x^2 +2)^2 ))dx=∫(x/(x^2 +2))dx−∫((x+1)/((x^2 +2)^2 ))dx =(1/2)∫((d(x^2 +2))/(x^2 +2))−(1/2)∫((d(x^2 +2))/((x^2 +2)^2 ))−∫(dx/((x^2 +2)^2 )) K=(1/2)ln(x^2 +2)+(1/(2(x^2 +2)))−(x/(4(x^2 +2)))−(1/4)×(1/(√2))arctan(x/(√2)) =(1/2)ln(x^2 +2)+((2−x)/(4(x^2 +2)))−(1/(4(√2)))arctan(x/(√2))+C

$$\mathrm{K}=\int\frac{\mathrm{x}\left(\mathrm{x}^{\mathrm{2}} +\mathrm{2}\right)−\left(\mathrm{x}+\mathrm{1}\right)}{\left(\mathrm{x}^{\mathrm{2}} +\mathrm{2}\right)^{\mathrm{2}} }\mathrm{dx}=\int\frac{\mathrm{x}}{\mathrm{x}^{\mathrm{2}} +\mathrm{2}}\mathrm{dx}−\int\frac{\mathrm{x}+\mathrm{1}}{\left(\mathrm{x}^{\mathrm{2}} +\mathrm{2}\right)^{\mathrm{2}} }\mathrm{dx} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\int\frac{\mathrm{d}\left(\mathrm{x}^{\mathrm{2}} +\mathrm{2}\right)}{\mathrm{x}^{\mathrm{2}} +\mathrm{2}}−\frac{\mathrm{1}}{\mathrm{2}}\int\frac{\mathrm{d}\left(\mathrm{x}^{\mathrm{2}} +\mathrm{2}\right)}{\left(\mathrm{x}^{\mathrm{2}} +\mathrm{2}\right)^{\mathrm{2}} }−\int\frac{\mathrm{dx}}{\left(\mathrm{x}^{\mathrm{2}} +\mathrm{2}\overset{\mathrm{2}} {\right)}} \\ $$$$\mathrm{K}=\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ln}\left(\mathrm{x}^{\mathrm{2}} +\mathrm{2}\right)+\frac{\mathrm{1}}{\mathrm{2}\left(\mathrm{x}^{\mathrm{2}} +\mathrm{2}\right)}−\frac{\mathrm{x}}{\mathrm{4}\left(\mathrm{x}^{\mathrm{2}} +\mathrm{2}\right)}−\frac{\mathrm{1}}{\mathrm{4}}×\frac{\mathrm{1}}{\sqrt{\mathrm{2}}}\mathrm{arctan}\frac{\mathrm{x}}{\sqrt{\mathrm{2}}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\boldsymbol{\mathrm{ln}}\left(\boldsymbol{\mathrm{x}}^{\mathrm{2}} +\mathrm{2}\right)+\frac{\mathrm{2}−\boldsymbol{\mathrm{x}}}{\mathrm{4}\left(\boldsymbol{\mathrm{x}}^{\mathrm{2}} +\mathrm{2}\right)}−\frac{\mathrm{1}}{\mathrm{4}\sqrt{\mathrm{2}}}\boldsymbol{\mathrm{arctan}}\frac{\boldsymbol{\mathrm{x}}}{\sqrt{\mathrm{2}}}+\mathrm{C} \\ $$

Answered by Dwaipayan Shikari last updated on 09/Jul/20

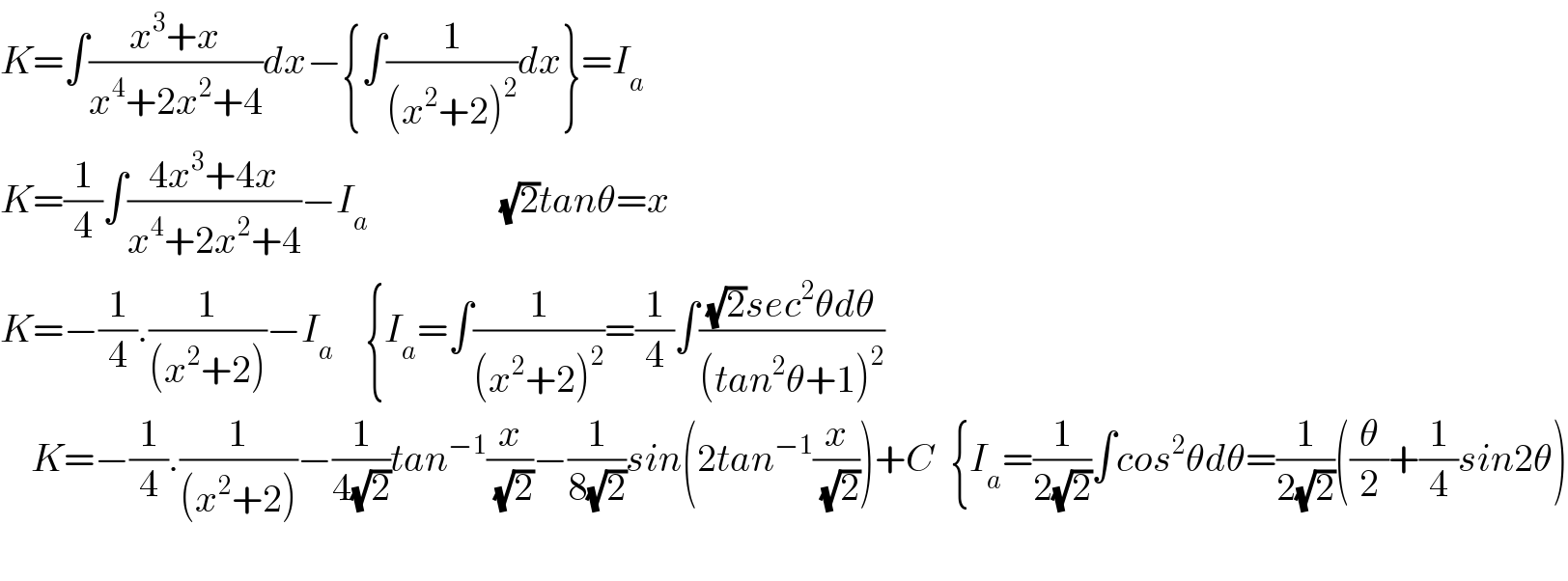
K=∫((x^3 +x)/(x^4 +2x^2 +4))dx−{∫(1/((x^2 +2)^2 ))dx}=I_a K=(1/4)∫((4x^3 +4x)/(x^4 +2x^2 +4))−I_(a ) (√2)tanθ=x K=−(1/4).(1/((x^2 +2)))−I_a {I_a =∫(1/((x^2 +2)^2 ))=(1/4)∫(((√2)sec^2 θdθ)/((tan^2 θ+1)^2 )) K=−(1/4).(1/((x^2 +2)))−(1/(4(√2)))tan^(−1) (x/(√2))−(1/(8(√2)))sin(2tan^(−1) (x/(√2)))+C {I_a =(1/(2(√2)))∫cos^2 θdθ=(1/(2(√2)))((θ/2)+(1/4)sin2θ)

$${K}=\int\frac{{x}^{\mathrm{3}} +{x}}{{x}^{\mathrm{4}} +\mathrm{2}{x}^{\mathrm{2}} +\mathrm{4}}{dx}−\left\{\int\frac{\mathrm{1}}{\left({x}^{\mathrm{2}} +\mathrm{2}\right)^{\mathrm{2}} }{dx}\right\}={I}_{{a}} \\ $$$${K}=\frac{\mathrm{1}}{\mathrm{4}}\int\frac{\mathrm{4}{x}^{\mathrm{3}} +\mathrm{4}{x}}{{x}^{\mathrm{4}} +\mathrm{2}{x}^{\mathrm{2}} +\mathrm{4}}−{I}_{{a}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:} \:\:\:\:\:\sqrt{\mathrm{2}}{tan}\theta={x} \\ $$$${K}=−\frac{\mathrm{1}}{\mathrm{4}}.\frac{\mathrm{1}}{\left({x}^{\mathrm{2}} +\mathrm{2}\right)}−{I}_{{a}} \:\:\:\:\left\{{I}_{{a}} =\int\frac{\mathrm{1}}{\left({x}^{\mathrm{2}} +\mathrm{2}\right)^{\mathrm{2}} }=\frac{\mathrm{1}}{\mathrm{4}}\int\frac{\sqrt{\mathrm{2}}{sec}^{\mathrm{2}} \theta{d}\theta}{\left({tan}^{\mathrm{2}} \theta+\mathrm{1}\right)^{\mathrm{2}} }\:\:\right. \\ $$$$\:\:\:\:{K}=−\frac{\mathrm{1}}{\mathrm{4}}.\frac{\mathrm{1}}{\left({x}^{\mathrm{2}} +\mathrm{2}\right)}−\frac{\mathrm{1}}{\mathrm{4}\sqrt{\mathrm{2}}}{tan}^{−\mathrm{1}} \frac{{x}}{\sqrt{\mathrm{2}}}−\frac{\mathrm{1}}{\mathrm{8}\sqrt{\mathrm{2}}}{sin}\left(\mathrm{2}{tan}^{−\mathrm{1}} \frac{{x}}{\sqrt{\mathrm{2}}}\right)+{C}\:\:\left\{{I}_{{a}} =\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{2}}}\int{cos}^{\mathrm{2}} \theta{d}\theta=\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{2}}}\left(\frac{\theta}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{4}}{sin}\mathrm{2}\theta\right)\right. \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\: \\ $$

Answered by mathmax by abdo last updated on 09/Jul/20

let f(a) =∫ (dx/(x(x^2 +x+a))) with a<(1/4) f^′ (a) =−∫ (dx/(x(x^2 +x+a)^2 )) and J =−f^′ (−1) let explicit f(a) first we decompose F(x) =(1/(x(x^2 +x+a))) x^2 +x+a =0 →Δ =1−4a >0 ⇒x_1 =((−1+(√(1−4a)))/2) x_2 =((−1−(√(1−4a)))/2) ⇒F(x) =(1/(x(x−x_1 )(x−x_2 )))=(α/x) +(β/(x−x_1 )) +(λ/(x−x_2 )) α =(1/a) , β =(1/(x_1 (√(1−4a)))) =(2/(((√(1−4a))−1)(√(1−4a))))) λ =(1/(x_2 (x_2 −x_1 ))) =(2/((−1−(√(1−4a)))(−(√(1−4a))))) =(2/((1+(√(1−4a)))(√(1−4a)))) ⇒ f(a) =αln∣x∣ +βln∣x−x_1 ∣+λ ln∣x−x_2 ∣ +c ⇒f(a) =(1/a)ln∣x∣ +(2/(((√(1−4a))−1)(√(1−4a))))ln∣x−((−1+(√(1−4a)))/2)∣ +(2/((1+(√(1−4a)))(√(1−4a))))ln∣x+((1+(√(1−4a)))/2)∣ +c rest to calculate f^′ (a) ...be continued...

$$\mathrm{let}\:\mathrm{f}\left(\mathrm{a}\right)\:=\int\:\:\frac{\mathrm{dx}}{\mathrm{x}\left(\mathrm{x}^{\mathrm{2}} \:+\mathrm{x}+\mathrm{a}\right)}\:\:\mathrm{with}\:\:\mathrm{a}<\frac{\mathrm{1}}{\mathrm{4}}\:\:\:\mathrm{f}^{'} \left(\mathrm{a}\right)\:=−\int\:\:\frac{\mathrm{dx}}{\mathrm{x}\left(\mathrm{x}^{\mathrm{2}} +\mathrm{x}+\mathrm{a}\right)^{\mathrm{2}} } \\ $$$$\mathrm{and}\:\mathrm{J}\:=−\mathrm{f}^{'} \left(−\mathrm{1}\right)\:\:\mathrm{let}\:\mathrm{explicit}\:\mathrm{f}\left(\mathrm{a}\right)\:\:\mathrm{first}\:\mathrm{we}\:\mathrm{decompose}\:\mathrm{F}\left(\mathrm{x}\right)\:=\frac{\mathrm{1}}{\mathrm{x}\left(\mathrm{x}^{\mathrm{2}} \:+\mathrm{x}+\mathrm{a}\right)} \\ $$$$\mathrm{x}^{\mathrm{2}} \:+\mathrm{x}+\mathrm{a}\:=\mathrm{0}\:\rightarrow\Delta\:=\mathrm{1}−\mathrm{4a}\:>\mathrm{0}\:\Rightarrow\mathrm{x}_{\mathrm{1}} =\frac{−\mathrm{1}+\sqrt{\mathrm{1}−\mathrm{4a}}}{\mathrm{2}} \\ $$$$\mathrm{x}_{\mathrm{2}} =\frac{−\mathrm{1}−\sqrt{\mathrm{1}−\mathrm{4a}}}{\mathrm{2}}\:\Rightarrow\mathrm{F}\left(\mathrm{x}\right)\:=\frac{\mathrm{1}}{\mathrm{x}\left(\mathrm{x}−\mathrm{x}_{\mathrm{1}} \right)\left(\mathrm{x}−\mathrm{x}_{\mathrm{2}} \right)}=\frac{\alpha}{\mathrm{x}}\:+\frac{\beta}{\mathrm{x}−\mathrm{x}_{\mathrm{1}} }\:+\frac{\lambda}{\mathrm{x}−\mathrm{x}_{\mathrm{2}} }\:\: \\ $$$$\alpha\:=\frac{\mathrm{1}}{\mathrm{a}}\:,\:\beta\:=\frac{\mathrm{1}}{\mathrm{x}_{\mathrm{1}} \sqrt{\mathrm{1}−\mathrm{4a}}}\:=\frac{\mathrm{2}}{\left.\left(\sqrt{\mathrm{1}−\mathrm{4a}}−\mathrm{1}\right)\sqrt{\mathrm{1}−\mathrm{4a}}\right)} \\ $$$$\lambda\:=\frac{\mathrm{1}}{\mathrm{x}_{\mathrm{2}} \left(\mathrm{x}_{\mathrm{2}} −\mathrm{x}_{\mathrm{1}} \right)}\:=\frac{\mathrm{2}}{\left(−\mathrm{1}−\sqrt{\mathrm{1}−\mathrm{4a}}\right)\left(−\sqrt{\mathrm{1}−\mathrm{4a}}\right)}\:=\frac{\mathrm{2}}{\left(\mathrm{1}+\sqrt{\mathrm{1}−\mathrm{4a}}\right)\sqrt{\mathrm{1}−\mathrm{4a}}}\:\Rightarrow \\ $$$$\mathrm{f}\left(\mathrm{a}\right)\:=\alpha\mathrm{ln}\mid\mathrm{x}\mid\:+\beta\mathrm{ln}\mid\mathrm{x}−\mathrm{x}_{\mathrm{1}} \mid+\lambda\:\mathrm{ln}\mid\mathrm{x}−\mathrm{x}_{\mathrm{2}} \mid\:+\mathrm{c} \\ $$$$\Rightarrow\mathrm{f}\left(\mathrm{a}\right)\:=\frac{\mathrm{1}}{\mathrm{a}}\mathrm{ln}\mid\mathrm{x}\mid\:+\frac{\mathrm{2}}{\left(\sqrt{\mathrm{1}−\mathrm{4a}}−\mathrm{1}\right)\sqrt{\mathrm{1}−\mathrm{4a}}}\mathrm{ln}\mid\mathrm{x}−\frac{−\mathrm{1}+\sqrt{\mathrm{1}−\mathrm{4a}}}{\mathrm{2}}\mid \\ $$$$+\frac{\mathrm{2}}{\left(\mathrm{1}+\sqrt{\mathrm{1}−\mathrm{4a}}\right)\sqrt{\mathrm{1}−\mathrm{4a}}}\mathrm{ln}\mid\mathrm{x}+\frac{\mathrm{1}+\sqrt{\mathrm{1}−\mathrm{4a}}}{\mathrm{2}}\mid\:+\mathrm{c}\:\:\mathrm{rest}\:\mathrm{to}\:\mathrm{calculate}\:\mathrm{f}^{'} \left(\mathrm{a}\right)\: \\ $$$$...\mathrm{be}\:\mathrm{continued}... \\ $$$$ \\ $$

Answered by mathmax by abdo last updated on 09/Jul/20

L =∫ (dx/(x+(√(1+x^2 )))) we do the cha7gement x =sht ⇒ L =∫ ((ch(t))/(sht +ch(t))) dt =∫ (((e^t +e^(−t) )/2)/(((e^t −e^(−t) )/2)+((e^t +e^(−t) )/2))) dt =∫ ((e^t +e^(−t) )/e^t ) dt =∫(1+e^(−2t) )dt =t −(1/2)e^(−2t) +c we have t =argsh(x) =ln(x+(√(1+x^2 ))) ⇒e^(2t) =(x+(√(1+x^2 )))^2 ⇒ L =ln(x+(√(1+x^2 )))−(1/(2(x+(√(1+x^2 )))^2 )) +C

$$\mathrm{L}\:=\int\:\:\frac{\mathrm{dx}}{\mathrm{x}+\sqrt{\mathrm{1}+\mathrm{x}^{\mathrm{2}} }}\:\:\mathrm{we}\:\mathrm{do}\:\mathrm{the}\:\mathrm{cha7gement}\:\:\mathrm{x}\:=\mathrm{sht}\:\Rightarrow \\ $$$$\mathrm{L}\:=\int\:\:\frac{\mathrm{ch}\left(\mathrm{t}\right)}{\mathrm{sht}\:+\mathrm{ch}\left(\mathrm{t}\right)}\:\mathrm{dt}\:=\int\:\:\:\frac{\frac{\mathrm{e}^{\mathrm{t}} +\mathrm{e}^{−\mathrm{t}} }{\mathrm{2}}}{\frac{\mathrm{e}^{\mathrm{t}} −\mathrm{e}^{−\mathrm{t}} }{\mathrm{2}}+\frac{\mathrm{e}^{\mathrm{t}} \:+\mathrm{e}^{−\mathrm{t}} }{\mathrm{2}}}\:\mathrm{dt} \\ $$$$=\int\:\:\frac{\mathrm{e}^{\mathrm{t}} \:+\mathrm{e}^{−\mathrm{t}} }{\mathrm{e}^{\mathrm{t}} }\:\mathrm{dt}\:=\int\left(\mathrm{1}+\mathrm{e}^{−\mathrm{2t}} \right)\mathrm{dt}\:=\mathrm{t}\:−\frac{\mathrm{1}}{\mathrm{2}}\mathrm{e}^{−\mathrm{2t}} \:+\mathrm{c} \\ $$$$\mathrm{we}\:\mathrm{have}\:\mathrm{t}\:=\mathrm{argsh}\left(\mathrm{x}\right)\:=\mathrm{ln}\left(\mathrm{x}+\sqrt{\mathrm{1}+\mathrm{x}^{\mathrm{2}} }\right)\:\Rightarrow\mathrm{e}^{\mathrm{2t}} \:=\left(\mathrm{x}+\sqrt{\mathrm{1}+\mathrm{x}^{\mathrm{2}} }\right)^{\mathrm{2}} \:\Rightarrow \\ $$$$\mathrm{L}\:=\mathrm{ln}\left(\mathrm{x}+\sqrt{\mathrm{1}+\mathrm{x}^{\mathrm{2}} }\right)−\frac{\mathrm{1}}{\mathrm{2}\left(\mathrm{x}+\sqrt{\mathrm{1}+\mathrm{x}^{\mathrm{2}} }\right)^{\mathrm{2}} }\:+\mathrm{C} \\ $$

Answered by mathmax by abdo last updated on 13/Jul/20

snother way for J =∫ (dx/(x(x^2 +x−1)^2 )) x^2 +x−1 =0→Δ =1+4 =5 ⇒α =((−1+(√5))/2) and β =((−1−(√5))/2) ⇒J =∫ (dx/(x(x−α)^2 (x−β)^2 )) =∫ (dx/(x(((x−α)/(x−β)))^2 (x−β)^4 )) we do the changement ((x−α)/(x−β))=t ⇒x−α =tx−βt ⇒(1−t)x =−βt +α ⇒x =((βt−α)/(t−1)) and x−β =((βt−α)/(t−1))−β =((βt−α−βt+β)/(t−1)) =((β−α)/(t−1)) ⇒ (dx/dt) =((β(t−1)−βt +α)/((t−1)^2 )) =((α−β)/((t−1)^2 )) ⇒ J =∫ ((α−β)/((t−1)^2 t^2 (((β−α)/(t−1)))^4 )) dt =(1/((α−β)^3 )) ∫ (((t−1)^4 )/((t−1)^2 t^2 ))dt =(1/((α−β)^3 )) ∫ (((t−1)^2 )/t^2 ) dt =(1/((α−β)^3 )) ∫ (((t^2 −2t +1)/t^2 ))dt =(1/((α−β)^3 )) ∫( 1−(2/t) +(1/t^2 ))dt =(1/((α−β)^3 )) { t−2ln∣t∣−(1/t)} +c =(1/(((√5))^3 )){ ((x−((−1+(√5))/2))/(x+((1+(√5))/2))) −2ln∣((x−((−1+(√5))/2))/(x+((1+(√5))/2)))∣−((x+((1+(√5))/2))/(x−((−1+(√5))/2)))} +c J=(1/(5(√5))){ ((2x+1−(√5))/(2x+1+(√5))) −2ln∣((2x+1−(√5))/(2x+1+(√5)))∣−((2x+1+(√5))/(2x+1−(√5)))} +c

$$\mathrm{snother}\:\mathrm{way}\:\mathrm{for}\:\mathrm{J}\:=\int\:\frac{\mathrm{dx}}{\mathrm{x}\left(\mathrm{x}^{\mathrm{2}} +\mathrm{x}−\mathrm{1}\right)^{\mathrm{2}} } \\ $$$$\mathrm{x}^{\mathrm{2}} \:+\mathrm{x}−\mathrm{1}\:=\mathrm{0}\rightarrow\Delta\:=\mathrm{1}+\mathrm{4}\:=\mathrm{5}\:\Rightarrow\alpha\:=\frac{−\mathrm{1}+\sqrt{\mathrm{5}}}{\mathrm{2}}\:\mathrm{and}\:\beta\:=\frac{−\mathrm{1}−\sqrt{\mathrm{5}}}{\mathrm{2}} \\ $$$$\Rightarrow\mathrm{J}\:=\int\:\:\frac{\mathrm{dx}}{\mathrm{x}\left(\mathrm{x}−\alpha\right)^{\mathrm{2}} \left(\mathrm{x}−\beta\right)^{\mathrm{2}} }\:=\int\:\:\frac{\mathrm{dx}}{\mathrm{x}\left(\frac{\mathrm{x}−\alpha}{\mathrm{x}−\beta}\right)^{\mathrm{2}} \left(\mathrm{x}−\beta\right)^{\mathrm{4}} }\:\:\mathrm{we}\:\mathrm{do}\:\mathrm{the}\:\mathrm{changement} \\ $$$$\frac{\mathrm{x}−\alpha}{\mathrm{x}−\beta}=\mathrm{t}\:\Rightarrow\mathrm{x}−\alpha\:=\mathrm{tx}−\beta\mathrm{t}\:\Rightarrow\left(\mathrm{1}−\mathrm{t}\right)\mathrm{x}\:=−\beta\mathrm{t}\:+\alpha\:\Rightarrow\mathrm{x}\:=\frac{\beta\mathrm{t}−\alpha}{\mathrm{t}−\mathrm{1}}\: \\ $$$$\mathrm{and}\:\mathrm{x}−\beta\:=\frac{\beta\mathrm{t}−\alpha}{\mathrm{t}−\mathrm{1}}−\beta\:=\frac{\beta\mathrm{t}−\alpha−\beta\mathrm{t}+\beta}{\mathrm{t}−\mathrm{1}}\:=\frac{\beta−\alpha}{\mathrm{t}−\mathrm{1}}\:\Rightarrow \\ $$$$\frac{\mathrm{dx}}{\mathrm{dt}}\:=\frac{\beta\left(\mathrm{t}−\mathrm{1}\right)−\beta\mathrm{t}\:+\alpha}{\left(\mathrm{t}−\mathrm{1}\right)^{\mathrm{2}} }\:=\frac{\alpha−\beta}{\left(\mathrm{t}−\mathrm{1}\right)^{\mathrm{2}} }\:\Rightarrow \\ $$$$\mathrm{J}\:=\int\:\frac{\alpha−\beta}{\left(\mathrm{t}−\mathrm{1}\right)^{\mathrm{2}} \:\mathrm{t}^{\mathrm{2}} \left(\frac{\beta−\alpha}{\mathrm{t}−\mathrm{1}}\right)^{\mathrm{4}} }\:\mathrm{dt}\:=\frac{\mathrm{1}}{\left(\alpha−\beta\right)^{\mathrm{3}} }\:\int\:\:\frac{\left(\mathrm{t}−\mathrm{1}\right)^{\mathrm{4}} }{\left(\mathrm{t}−\mathrm{1}\right)^{\mathrm{2}} \:\mathrm{t}^{\mathrm{2}} }\mathrm{dt} \\ $$$$=\frac{\mathrm{1}}{\left(\alpha−\beta\right)^{\mathrm{3}} }\:\int\:\:\frac{\left(\mathrm{t}−\mathrm{1}\right)^{\mathrm{2}} }{\mathrm{t}^{\mathrm{2}} }\:\mathrm{dt}\:=\frac{\mathrm{1}}{\left(\alpha−\beta\right)^{\mathrm{3}} }\:\int\:\left(\frac{\mathrm{t}^{\mathrm{2}} −\mathrm{2t}\:+\mathrm{1}}{\mathrm{t}^{\mathrm{2}} }\right)\mathrm{dt} \\ $$$$=\frac{\mathrm{1}}{\left(\alpha−\beta\right)^{\mathrm{3}} }\:\int\left(\:\mathrm{1}−\frac{\mathrm{2}}{\mathrm{t}}\:+\frac{\mathrm{1}}{\mathrm{t}^{\mathrm{2}} }\right)\mathrm{dt}\:=\frac{\mathrm{1}}{\left(\alpha−\beta\right)^{\mathrm{3}} }\:\left\{\:\mathrm{t}−\mathrm{2ln}\mid\mathrm{t}\mid−\frac{\mathrm{1}}{\mathrm{t}}\right\}\:+\mathrm{c} \\ $$$$=\frac{\mathrm{1}}{\left(\sqrt{\mathrm{5}}\right)^{\mathrm{3}} }\left\{\:\frac{\mathrm{x}−\frac{−\mathrm{1}+\sqrt{\mathrm{5}}}{\mathrm{2}}}{\mathrm{x}+\frac{\mathrm{1}+\sqrt{\mathrm{5}}}{\mathrm{2}}}\:−\mathrm{2ln}\mid\frac{\mathrm{x}−\frac{−\mathrm{1}+\sqrt{\mathrm{5}}}{\mathrm{2}}}{\mathrm{x}+\frac{\mathrm{1}+\sqrt{\mathrm{5}}}{\mathrm{2}}}\mid−\frac{\mathrm{x}+\frac{\mathrm{1}+\sqrt{\mathrm{5}}}{\mathrm{2}}}{\mathrm{x}−\frac{−\mathrm{1}+\sqrt{\mathrm{5}}}{\mathrm{2}}}\right\}\:+\mathrm{c} \\ $$$$\mathrm{J}=\frac{\mathrm{1}}{\mathrm{5}\sqrt{\mathrm{5}}}\left\{\:\frac{\mathrm{2x}+\mathrm{1}−\sqrt{\mathrm{5}}}{\mathrm{2x}+\mathrm{1}+\sqrt{\mathrm{5}}}\:−\mathrm{2ln}\mid\frac{\mathrm{2x}+\mathrm{1}−\sqrt{\mathrm{5}}}{\mathrm{2x}+\mathrm{1}+\sqrt{\mathrm{5}}}\mid−\frac{\mathrm{2x}+\mathrm{1}+\sqrt{\mathrm{5}}}{\mathrm{2x}+\mathrm{1}−\sqrt{\mathrm{5}}}\right\}\:+\mathrm{c} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com