Question and Answers Forum

All Questions      Topic List

Integration Questions

Previous in All Question      Next in All Question      

Previous in Integration      Next in Integration      

Question Number 102470 by  M±th+et+s last updated on 09/Jul/20

∫(dx/(x^(10) +x^2 ))

$$\int\frac{{dx}}{{x}^{\mathrm{10}} +{x}^{\mathrm{2}} } \\ $$$$ \\ $$

Answered by Ar Brandon last updated on 09/Jul/20

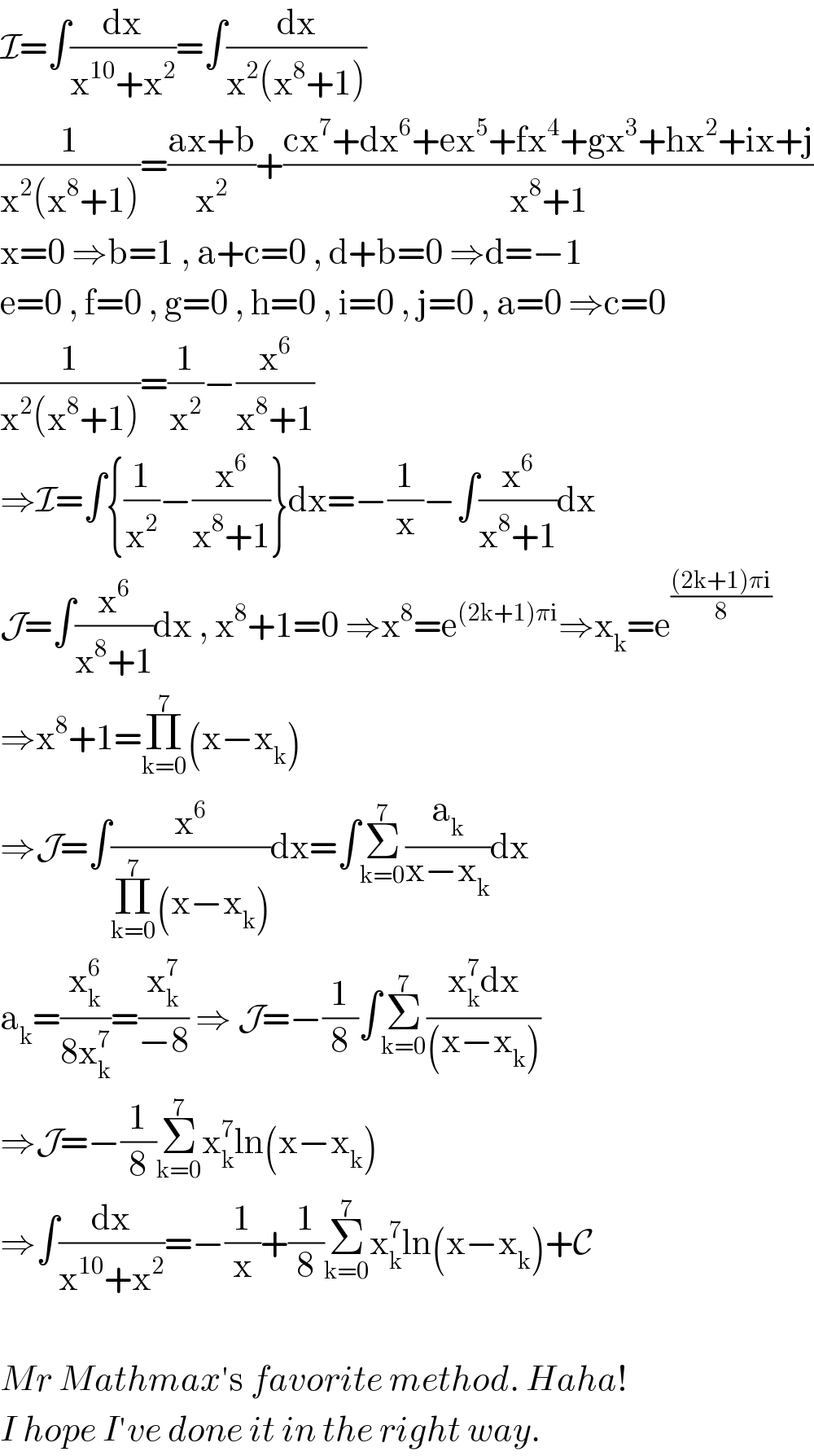
I=∫(dx/(x^(10) +x^2 ))=∫(dx/(x^2 (x^8 +1))) (1/(x^2 (x^8 +1)))=((ax+b)/x^2 )+((cx^7 +dx^6 +ex^5 +fx^4 +gx^3 +hx^2 +ix+j)/(x^8 +1)) x=0 ⇒b=1 , a+c=0 , d+b=0 ⇒d=−1 e=0 , f=0 , g=0 , h=0 , i=0 , j=0 , a=0 ⇒c=0 (1/(x^2 (x^8 +1)))=(1/x^2 )−(x^6 /(x^8 +1)) ⇒I=∫{(1/x^2 )−(x^6 /(x^8 +1))}dx=−(1/x)−∫(x^6 /(x^8 +1))dx J=∫(x^6 /(x^8 +1))dx , x^8 +1=0 ⇒x^8 =e^((2k+1)πi) ⇒x_k =e^((((2k+1)πi)/8) ) ⇒x^8 +1=Π_(k=0) ^7 (x−x_k ) ⇒J=∫(x^6 /(Π_(k=0) ^7 (x−x_k )))dx=∫Σ_(k=0) ^7 (a_k /(x−x_k ))dx a_k =(x_k ^6 /(8x_k ^7 ))=(x_k ^7 /(−8)) ⇒ J=−(1/8)∫Σ_(k=0) ^7 ((x_k ^7 dx)/((x−x_k ))) ⇒J=−(1/8)Σ_(k=0) ^7 x_k ^7 ln(x−x_k ) ⇒∫(dx/(x^(10) +x^2 ))=−(1/x)+(1/8)Σ_(k=0) ^7 x_k ^7 ln(x−x_k )+C Mr Mathmax′s favorite method. Haha! I hope I′ve done it in the right way.

$$\mathcal{I}=\int\frac{\mathrm{dx}}{\mathrm{x}^{\mathrm{10}} +\mathrm{x}^{\mathrm{2}} }=\int\frac{\mathrm{dx}}{\mathrm{x}^{\mathrm{2}} \left(\mathrm{x}^{\mathrm{8}} +\mathrm{1}\right)} \\ $$$$\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{2}} \left(\mathrm{x}^{\mathrm{8}} +\mathrm{1}\right)}=\frac{\mathrm{ax}+\mathrm{b}}{\mathrm{x}^{\mathrm{2}} }+\frac{\mathrm{cx}^{\mathrm{7}} +\mathrm{dx}^{\mathrm{6}} +\mathrm{ex}^{\mathrm{5}} +\mathrm{fx}^{\mathrm{4}} +\mathrm{gx}^{\mathrm{3}} +\mathrm{hx}^{\mathrm{2}} +\mathrm{ix}+\mathrm{j}}{\mathrm{x}^{\mathrm{8}} +\mathrm{1}} \\ $$$$\mathrm{x}=\mathrm{0}\:\Rightarrow\mathrm{b}=\mathrm{1}\:,\:\mathrm{a}+\mathrm{c}=\mathrm{0}\:,\:\mathrm{d}+\mathrm{b}=\mathrm{0}\:\Rightarrow\mathrm{d}=−\mathrm{1} \\ $$$$\mathrm{e}=\mathrm{0}\:,\:\mathrm{f}=\mathrm{0}\:,\:\mathrm{g}=\mathrm{0}\:,\:\mathrm{h}=\mathrm{0}\:,\:\mathrm{i}=\mathrm{0}\:,\:\mathrm{j}=\mathrm{0}\:,\:\mathrm{a}=\mathrm{0}\:\Rightarrow\mathrm{c}=\mathrm{0} \\ $$$$\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{2}} \left(\mathrm{x}^{\mathrm{8}} +\mathrm{1}\right)}=\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{2}} }−\frac{\mathrm{x}^{\mathrm{6}} }{\mathrm{x}^{\mathrm{8}} +\mathrm{1}} \\ $$$$\Rightarrow\mathcal{I}=\int\left\{\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{2}} }−\frac{\mathrm{x}^{\mathrm{6}} }{\mathrm{x}^{\mathrm{8}} +\mathrm{1}}\right\}\mathrm{dx}=−\frac{\mathrm{1}}{\mathrm{x}}−\int\frac{\mathrm{x}^{\mathrm{6}} }{\mathrm{x}^{\mathrm{8}} +\mathrm{1}}\mathrm{dx} \\ $$$$\mathcal{J}=\int\frac{\mathrm{x}^{\mathrm{6}} }{\mathrm{x}^{\mathrm{8}} +\mathrm{1}}\mathrm{dx}\:,\:\mathrm{x}^{\mathrm{8}} +\mathrm{1}=\mathrm{0}\:\Rightarrow\mathrm{x}^{\mathrm{8}} =\mathrm{e}^{\left(\mathrm{2k}+\mathrm{1}\right)\pi\mathrm{i}} \Rightarrow\mathrm{x}_{\mathrm{k}} =\mathrm{e}^{\frac{\left(\mathrm{2k}+\mathrm{1}\right)\pi\mathrm{i}}{\mathrm{8}}\:} \\ $$$$\Rightarrow\mathrm{x}^{\mathrm{8}} +\mathrm{1}=\underset{\mathrm{k}=\mathrm{0}} {\overset{\mathrm{7}} {\prod}}\left(\mathrm{x}−\mathrm{x}_{\mathrm{k}} \right) \\ $$$$\Rightarrow\mathcal{J}=\int\frac{\mathrm{x}^{\mathrm{6}} }{\underset{\mathrm{k}=\mathrm{0}} {\overset{\mathrm{7}} {\prod}}\left(\mathrm{x}−\mathrm{x}_{\mathrm{k}} \right)}\mathrm{dx}=\int\underset{\mathrm{k}=\mathrm{0}} {\overset{\mathrm{7}} {\sum}}\frac{\mathrm{a}_{\mathrm{k}} }{\mathrm{x}−\mathrm{x}_{\mathrm{k}} }\mathrm{dx} \\ $$$$\mathrm{a}_{\mathrm{k}} =\frac{\mathrm{x}_{\mathrm{k}} ^{\mathrm{6}} }{\mathrm{8x}_{\mathrm{k}} ^{\mathrm{7}} }=\frac{\mathrm{x}_{\mathrm{k}} ^{\mathrm{7}} }{−\mathrm{8}}\:\Rightarrow\:\mathcal{J}=−\frac{\mathrm{1}}{\mathrm{8}}\int\underset{\mathrm{k}=\mathrm{0}} {\overset{\mathrm{7}} {\sum}}\frac{\mathrm{x}_{\mathrm{k}} ^{\mathrm{7}} \mathrm{dx}}{\left(\mathrm{x}−\mathrm{x}_{\mathrm{k}} \right)} \\ $$$$\Rightarrow\mathcal{J}=−\frac{\mathrm{1}}{\mathrm{8}}\underset{\mathrm{k}=\mathrm{0}} {\overset{\mathrm{7}} {\sum}}\mathrm{x}_{\mathrm{k}} ^{\mathrm{7}} \mathrm{ln}\left(\mathrm{x}−\mathrm{x}_{\mathrm{k}} \right) \\ $$$$\Rightarrow\int\frac{\mathrm{dx}}{\mathrm{x}^{\mathrm{10}} +\mathrm{x}^{\mathrm{2}} }=−\frac{\mathrm{1}}{\mathrm{x}}+\frac{\mathrm{1}}{\mathrm{8}}\underset{\mathrm{k}=\mathrm{0}} {\overset{\mathrm{7}} {\sum}}\mathrm{x}_{\mathrm{k}} ^{\mathrm{7}} \mathrm{ln}\left(\mathrm{x}−\mathrm{x}_{\mathrm{k}} \right)+\mathcal{C} \\ $$$$ \\ $$$${Mr}\:{Mathmax}'\mathrm{s}\:{favorite}\:{method}.\:{Haha}! \\ $$$${I}\:{hope}\:{I}'{ve}\:{done}\:{it}\:{in}\:{the}\:{right}\:{way}. \\ $$

Commented by  M±th+et+s last updated on 09/Jul/20

well done sir

$${well}\:{done}\:{sir} \\ $$

Commented by Ar Brandon last updated on 09/Jul/20

��

Commented by mathmax by abdo last updated on 09/Jul/20

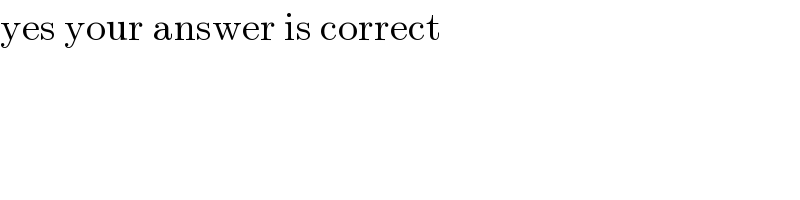
yes your answer is correct

$$\mathrm{yes}\:\mathrm{your}\:\mathrm{answer}\:\mathrm{is}\:\mathrm{correct} \\ $$

Commented by floor(10²Eta[1]) last updated on 09/Jul/20

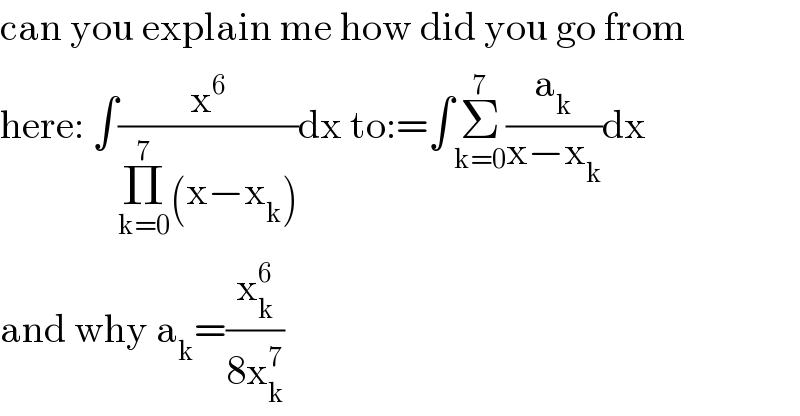
can you explain me how did you go from here: ∫(x^6 /(Π_(k=0) ^7 (x−x_k )))dx to:=∫Σ_(k=0) ^7 (a_k /(x−x_k ))dx and why a_k =(x_k ^6 /(8x_k ^7 ))

$$\mathrm{can}\:\mathrm{you}\:\mathrm{explain}\:\mathrm{me}\:\mathrm{how}\:\mathrm{did}\:\mathrm{you}\:\mathrm{go}\:\mathrm{from} \\ $$$$\mathrm{here}:\:\int\frac{\mathrm{x}^{\mathrm{6}} }{\underset{\mathrm{k}=\mathrm{0}} {\overset{\mathrm{7}} {\prod}}\left(\mathrm{x}−\mathrm{x}_{\mathrm{k}} \right)}\mathrm{dx}\:\mathrm{to}:=\int\underset{\mathrm{k}=\mathrm{0}} {\overset{\mathrm{7}} {\sum}}\frac{\mathrm{a}_{\mathrm{k}} }{\mathrm{x}−\mathrm{x}_{\mathrm{k}} }\mathrm{dx} \\ $$$$\mathrm{and}\:\mathrm{why}\:\mathrm{a}_{\mathrm{k}} =\frac{\mathrm{x}_{\mathrm{k}} ^{\mathrm{6}} }{\mathrm{8x}_{\mathrm{k}} ^{\mathrm{7}} } \\ $$

Commented by Ar Brandon last updated on 09/Jul/20

Hi ! Mathmax explained this to me in Q86484. I guess you have a look at it.

$$\mathrm{Hi}\:!\:\mathrm{Mathmax}\:\mathrm{explained}\:\mathrm{this}\:\mathrm{to}\:\mathrm{me}\:\mathrm{in}\:\mathrm{Q86484}. \\ $$$$\mathrm{I}\:\mathrm{guess}\:\mathrm{you}\:\mathrm{have}\:\mathrm{a}\:\mathrm{look}\:\mathrm{at}\:\mathrm{it}. \\ $$

Commented by Ar Brandon last updated on 09/Jul/20

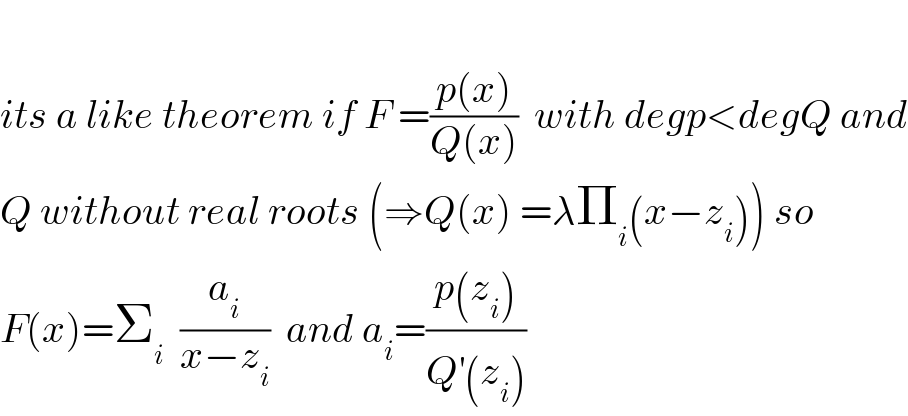
its a like theorem if F =((p(x))/(Q(x))) with degp<degQ and Q without real roots (⇒Q(x) =λΠ_i (x−z_i )) so F(x)=Σ_i (a_i /(x−z_i )) and a_i =((p(z_i ))/(Q^′ (z_i )))

$$ \\ $$$${its}\:{a}\:{like}\:{theorem}\:{if}\:{F}\:=\frac{{p}\left({x}\right)}{{Q}\left({x}\right)}\:\:{with}\:{degp}<{degQ}\:{and} \\ $$$${Q}\:{without}\:{real}\:{roots}\:\left(\Rightarrow{Q}\left({x}\right)\:=\lambda\prod_{{i}} \left({x}−{z}_{{i}} \right)\right)\:{so} \\ $$$${F}\left({x}\right)=\sum_{{i}} \:\:\frac{{a}_{{i}} }{{x}−{z}_{{i}} }\:\:{and}\:{a}_{{i}} =\frac{{p}\left({z}_{{i}} \right)}{{Q}^{'} \left({z}_{{i}} \right)} \\ $$

Commented by floor(10²Eta[1]) last updated on 09/Jul/20

thanks! that′s really nice, do you know where i can see the demonstration of this?

$$\mathrm{thanks}!\:\mathrm{that}'\mathrm{s}\:\mathrm{really}\:\mathrm{nice},\:\mathrm{do}\:\mathrm{you}\:\mathrm{know}\:\mathrm{where}\: \\ $$$$\mathrm{i}\:\mathrm{can}\:\mathrm{see}\:\mathrm{the}\:\mathrm{demonstration}\:\mathrm{of}\:\mathrm{this}? \\ $$

Commented by Ar Brandon last updated on 09/Jul/20

Thanks for your approval Sir Mathmax. ��

Commented by Ar Brandon last updated on 09/Jul/20

No idea, I don't know where you can find this demo. Maybe a little search on Google might help.��

Commented by mathmax by abdo last updated on 10/Jul/20

you are welcome sir

$$\mathrm{you}\:\mathrm{are}\:\mathrm{welcome}\:\mathrm{sir} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com