Question and Answers Forum

All Questions      Topic List

Vector Calculus Questions

Previous in All Question      Next in All Question      

Previous in Vector Calculus      Next in Vector Calculus      

Question Number 102474 by pticantor last updated on 09/Jul/20

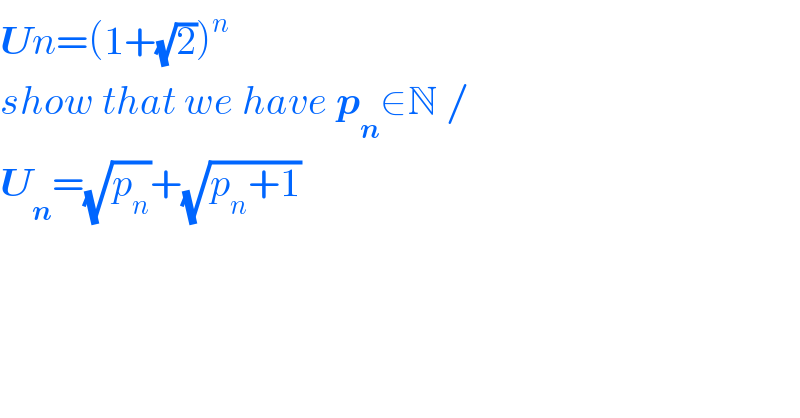
Un=(1+(√2))^n show that we have p_n ∈N / U_n =(√p_n )+(√(p_n +1))

$$\boldsymbol{{U}}{n}=\left(\mathrm{1}+\sqrt{\mathrm{2}}\right)^{{n}} \\ $$$${show}\:{that}\:{we}\:{have}\:\boldsymbol{{p}}_{\boldsymbol{{n}}} \in\mathbb{N}\:/ \\ $$$$\boldsymbol{{U}}_{\boldsymbol{{n}}} =\sqrt{{p}_{{n}} }+\sqrt{{p}_{{n}} +\mathrm{1}} \\ $$

Answered by ~blr237~ last updated on 09/Jul/20

observe that (1/U_n )=(−1)^n (1−(√2))^n and that there exist a_n ,b_n ∈N such as U_n =a_n +b_n (√2) and (1/U_n )=(−1)^n (a_n −b_n (√2)) and U_n ^2 =U_(2n) . So (U_n ^ +(1/U_n ))^2 = 2+U_(2n) +(1/U_(2n) )=2 +2a_(2n) (U_n −(1/U_n ))^2 =−2+U_(2n) +(1/U_(2n) ) =−2+2a_(2n) we have a_(n+1) +b_(n+1) (√2) =(1+(√2))(a_n +b_n (√2) ) lead to a_(n+1) =a_n +2b_n . So such as a_1 =1 (odd ) , a_n is always odd So there exist c_n ∈N / a_n =2c_n +1 Then (U_n +(1/U_n ))^2 =2+2(2c_(2n) +1)=4(c_(2n) +1) (U_n −(1/U_n ))^2 =−2+2(2c_(2n) +1)=4c_(2n) By adding the two square root U_n =(√c_(2n) ) +(√(c_(2n) +1)) take p_n =c_(2n)

$$\:{observe}\:{that}\:\frac{\mathrm{1}}{{U}_{{n}} }=\left(−\mathrm{1}\right)^{{n}} \left(\mathrm{1}−\sqrt{\mathrm{2}}\right)^{{n}} \:\:{and}\:{that}\:{there}\:{exist}\: \\ $$$${a}_{{n}} \:,{b}_{{n}} \in\mathbb{N}\:\:{such}\:{as}\:\:\:{U}_{{n}} ={a}_{{n}} +{b}_{{n}} \sqrt{\mathrm{2}}\:\:\:\:{and}\:\:\frac{\mathrm{1}}{{U}_{{n}} }=\left(−\mathrm{1}\right)^{{n}} \left({a}_{{n}} −{b}_{{n}} \sqrt{\mathrm{2}}\right) \\ $$$${and}\:\:{U}_{{n}} ^{\mathrm{2}} ={U}_{\mathrm{2}{n}} \:. \\ $$$${So}\:\:\left({U}_{{n}} ^{} +\frac{\mathrm{1}}{{U}_{{n}} }\right)^{\mathrm{2}} =\:\mathrm{2}+{U}_{\mathrm{2}{n}} +\frac{\mathrm{1}}{{U}_{\mathrm{2}{n}} }=\mathrm{2}\:+\mathrm{2}{a}_{\mathrm{2}{n}} \: \\ $$$$\left({U}_{{n}} −\frac{\mathrm{1}}{{U}_{{n}} }\right)^{\mathrm{2}} =−\mathrm{2}+{U}_{\mathrm{2}{n}} +\frac{\mathrm{1}}{{U}_{\mathrm{2}{n}} }\:=−\mathrm{2}+\mathrm{2}{a}_{\mathrm{2}{n}} \\ $$$${we}\:{have}\:\:{a}_{{n}+\mathrm{1}} +{b}_{{n}+\mathrm{1}} \sqrt{\mathrm{2}}\:=\left(\mathrm{1}+\sqrt{\mathrm{2}}\right)\left({a}_{{n}} +{b}_{{n}} \sqrt{\mathrm{2}}\:\right)\:{lead}\:{to} \\ $$$${a}_{{n}+\mathrm{1}} ={a}_{{n}} +\mathrm{2}{b}_{{n}} \:.\:{So}\:\:{such}\:{as}\:{a}_{\mathrm{1}} =\mathrm{1}\:\left({odd}\:\right)\:,\:{a}_{{n}} \:{is}\:{always}\:{odd}\: \\ $$$${So}\:{there}\:{exist}\:\:{c}_{{n}} \:\in\mathbb{N}\:\:/\:{a}_{{n}} =\mathrm{2}{c}_{{n}} +\mathrm{1} \\ $$$${Then}\:\:\:\:\left({U}_{{n}} +\frac{\mathrm{1}}{{U}_{{n}} }\right)^{\mathrm{2}} =\mathrm{2}+\mathrm{2}\left(\mathrm{2}{c}_{\mathrm{2}{n}} +\mathrm{1}\right)=\mathrm{4}\left({c}_{\mathrm{2}{n}} +\mathrm{1}\right) \\ $$$$\:\left({U}_{{n}} −\frac{\mathrm{1}}{{U}_{{n}} }\right)^{\mathrm{2}} =−\mathrm{2}+\mathrm{2}\left(\mathrm{2}{c}_{\mathrm{2}{n}} +\mathrm{1}\right)=\mathrm{4}{c}_{\mathrm{2}{n}} \: \\ $$$${By}\:{adding}\:{the}\:{two}\:{square}\:{root}\: \\ $$$${U}_{{n}} =\sqrt{{c}_{\mathrm{2}{n}} }\:+\sqrt{{c}_{\mathrm{2}{n}} +\mathrm{1}}\:\:\:\:{take}\:\:{p}_{{n}} ={c}_{\mathrm{2}{n}} \\ $$$$ \\ $$$$ \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com