Question and Answers Forum

All Questions      Topic List

Number Theory Questions

Previous in All Question      Next in All Question      

Previous in Number Theory      Next in Number Theory      

Question Number 102588 by bobhans last updated on 10/Jul/20

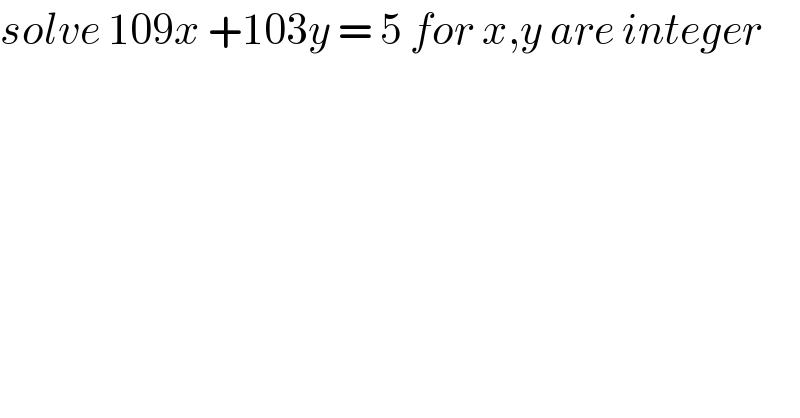
solve 109x +103y = 5 for x,y are integer

$${solve}\:\mathrm{109}{x}\:+\mathrm{103}{y}\:=\:\mathrm{5}\:{for}\:{x},{y}\:{are}\:{integer} \\ $$

Commented by mr W last updated on 10/Jul/20

see Q44819

$${see}\:{Q}\mathrm{44819} \\ $$

Commented by mr W last updated on 10/Jul/20

see also Q19198

$${see}\:{also}\:{Q}\mathrm{19198} \\ $$

Commented by bobhans last updated on 10/Jul/20

coll sir

$${coll}\:{sir} \\ $$

Answered by 1549442205 last updated on 10/Jul/20

y=((5−109x)/(103))=((5−6x)/(103))−x.Put ((5−6x)/(103))=a(a∈Z) ⇒5−6x=103a⇔x=((5−103a)/6)=−17a+((5−a)/6) Put ((5−a)/6)=b⇒a=5−6b.From this we get x=−17a+b=103b−85,y=−x+a =−109b+90.Thus,the roots of eqs be { ((x=103b−85)),((y=−109b+90)) :}(b∈Z)

$$\mathrm{y}=\frac{\mathrm{5}−\mathrm{109x}}{\mathrm{103}}=\frac{\mathrm{5}−\mathrm{6x}}{\mathrm{103}}−\mathrm{x}.\mathrm{Put}\:\frac{\mathrm{5}−\mathrm{6x}}{\mathrm{103}}=\mathrm{a}\left(\mathrm{a}\in\mathbb{Z}\right) \\ $$$$\Rightarrow\mathrm{5}−\mathrm{6x}=\mathrm{103a}\Leftrightarrow\mathrm{x}=\frac{\mathrm{5}−\mathrm{103a}}{\mathrm{6}}=−\mathrm{17a}+\frac{\mathrm{5}−\mathrm{a}}{\mathrm{6}} \\ $$$$\mathrm{Put}\:\frac{\mathrm{5}−\mathrm{a}}{\mathrm{6}}=\mathrm{b}\Rightarrow\mathrm{a}=\mathrm{5}−\mathrm{6b}.\mathrm{From}\:\mathrm{this}\:\mathrm{we} \\ $$$$\mathrm{get}\:\mathrm{x}=−\mathrm{17a}+\mathrm{b}=\mathrm{103b}−\mathrm{85},\mathrm{y}=−\mathrm{x}+\mathrm{a} \\ $$$$=−\mathrm{109b}+\mathrm{90}.\mathrm{Thus},\mathrm{the}\:\mathrm{roots}\:\mathrm{of}\:\mathrm{eqs}\:\mathrm{be} \\ $$$$\begin{cases}{\boldsymbol{\mathrm{x}}=\mathrm{103}\boldsymbol{\mathrm{b}}−\mathrm{85}}\\{\boldsymbol{\mathrm{y}}=−\mathrm{109}\boldsymbol{\mathrm{b}}+\mathrm{90}}\end{cases}\left(\boldsymbol{\mathrm{b}}\in\mathbb{Z}\right) \\ $$$$ \\ $$

Answered by bemath last updated on 10/Jul/20

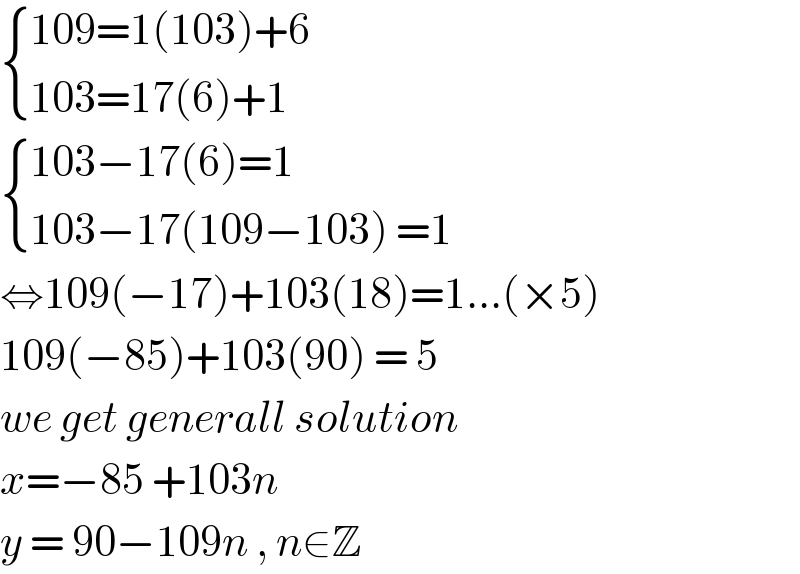
{ ((109=1(103)+6)),((103=17(6)+1)) :} { ((103−17(6)=1)),((103−17(109−103) =1)) :} ⇔109(−17)+103(18)=1...(×5) 109(−85)+103(90) = 5 we get generall solution x=−85 +103n y = 90−109n , n∈Z

$$\begin{cases}{\mathrm{109}=\mathrm{1}\left(\mathrm{103}\right)+\mathrm{6}}\\{\mathrm{103}=\mathrm{17}\left(\mathrm{6}\right)+\mathrm{1}}\end{cases} \\ $$$$\begin{cases}{\mathrm{103}−\mathrm{17}\left(\mathrm{6}\right)=\mathrm{1}}\\{\mathrm{103}−\mathrm{17}\left(\mathrm{109}−\mathrm{103}\right)\:=\mathrm{1}}\end{cases} \\ $$$$\Leftrightarrow\mathrm{109}\left(−\mathrm{17}\right)+\mathrm{103}\left(\mathrm{18}\right)=\mathrm{1}...\left(×\mathrm{5}\right) \\ $$$$\mathrm{109}\left(−\mathrm{85}\right)+\mathrm{103}\left(\mathrm{90}\right)\:=\:\mathrm{5} \\ $$$${we}\:{get}\:{generall}\:{solution} \\ $$$${x}=−\mathrm{85}\:+\mathrm{103}{n} \\ $$$${y}\:=\:\mathrm{90}−\mathrm{109}{n}\:,\:{n}\in\mathbb{Z} \\ $$

Answered by PRITHWISH SEN 2 last updated on 10/Jul/20

109x+103y=5 It is a diophantine equation ∵ gcd(109,103)=1 then there exists two integers u and v such that 109u+103v=1 here u=−85 amd v=90 then 109x+103y=−109.85+103.90 ⇒109(x+85)=−103(y−90) ((x+85)/(−103)) = ((y−90)/(109)) = t (integer) ∵ gcd(109,103)=1 then103∣(x+85) and 109∣(y−90) ∴ x =−103t−85 y = 109t+90

$$\mathrm{109x}+\mathrm{103y}=\mathrm{5}\:\:\:\:\boldsymbol{\mathrm{It}}\:\boldsymbol{\mathrm{is}}\:\boldsymbol{\mathrm{a}}\:\boldsymbol{\mathrm{diophantine}}\:\boldsymbol{\mathrm{equation}} \\ $$$$\because\:\mathrm{gcd}\left(\mathrm{109},\mathrm{103}\right)=\mathrm{1} \\ $$$$\mathrm{then}\:\mathrm{there}\:\mathrm{exists}\:\mathrm{two}\:\mathrm{integers}\:\mathrm{u}\:\mathrm{and}\:\mathrm{v}\:\mathrm{such}\:\mathrm{that} \\ $$$$\mathrm{109u}+\mathrm{103v}=\mathrm{1} \\ $$$$\mathrm{here}\:\mathrm{u}=−\mathrm{85}\:\mathrm{amd}\:\mathrm{v}=\mathrm{90} \\ $$$$\mathrm{then}\:\mathrm{109x}+\mathrm{103y}=−\mathrm{109}.\mathrm{85}+\mathrm{103}.\mathrm{90} \\ $$$$\Rightarrow\mathrm{109}\left(\mathrm{x}+\mathrm{85}\right)=−\mathrm{103}\left(\mathrm{y}−\mathrm{90}\right) \\ $$$$\frac{\mathrm{x}+\mathrm{85}}{−\mathrm{103}}\:=\:\frac{\mathrm{y}−\mathrm{90}}{\mathrm{109}}\:\:=\:\mathrm{t}\:\left(\boldsymbol{\mathrm{integer}}\right)\: \\ $$$$\:\because\:\mathrm{gcd}\left(\mathrm{109},\mathrm{103}\right)=\mathrm{1}\:\mathrm{then103}\mid\left(\mathrm{x}+\mathrm{85}\right)\:\mathrm{and}\:\mathrm{109}\mid\left(\mathrm{y}−\mathrm{90}\right) \\ $$$$\therefore\:\boldsymbol{\mathrm{x}}\:=−\mathrm{103}\boldsymbol{\mathrm{t}}−\mathrm{85} \\ $$$$\:\:\:\:\:\boldsymbol{\mathrm{y}}\:=\:\mathrm{109}\boldsymbol{\mathrm{t}}+\mathrm{90} \\ $$$$ \\ $$

Answered by bobhans last updated on 10/Jul/20

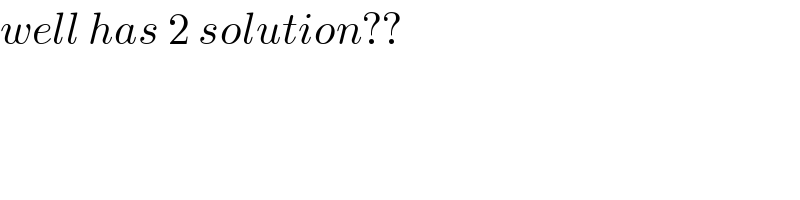
well has 2 solution??

$${well}\:{has}\:\mathrm{2}\:{solution}??\: \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com