Question and Answers Forum

All Questions      Topic List

Others Questions

Previous in All Question      Next in All Question      

Previous in Others      Next in Others      

Question Number 102598 by dw last updated on 10/Jul/20

Answered by mr W last updated on 10/Jul/20

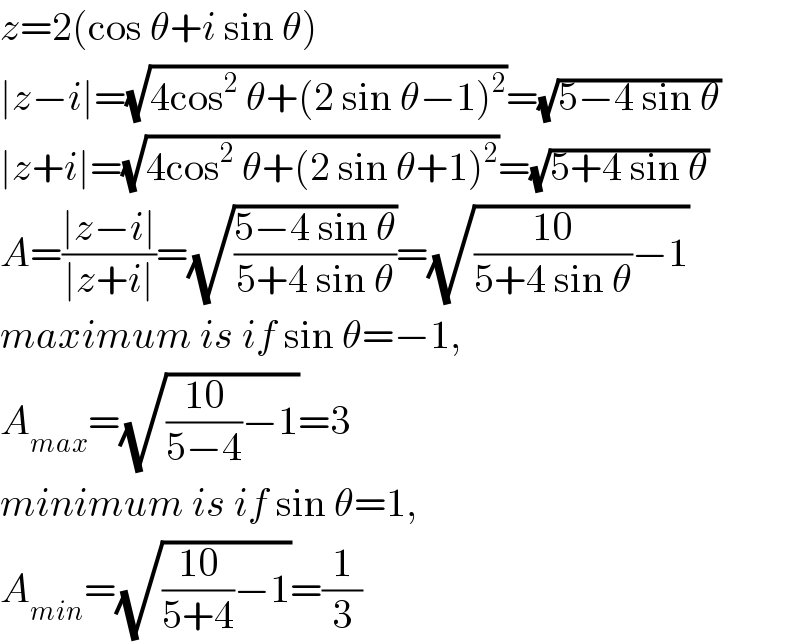
z=2(cos θ+i sin θ) ∣z−i∣=(√(4cos^2 θ+(2 sin θ−1)^2 ))=(√(5−4 sin θ)) ∣z+i∣=(√(4cos^2 θ+(2 sin θ+1)^2 ))=(√(5+4 sin θ)) A=((∣z−i∣)/(∣z+i∣))=(√((5−4 sin θ)/(5+4 sin θ)))=(√(((10)/(5+4 sin θ))−1)) maximum is if sin θ=−1, A_(max) =(√(((10)/(5−4))−1))=3 minimum is if sin θ=1, A_(min) =(√(((10)/(5+4))−1))=(1/3)

$${z}=\mathrm{2}\left(\mathrm{cos}\:\theta+{i}\:\mathrm{sin}\:\theta\right) \\ $$$$\mid{z}−{i}\mid=\sqrt{\mathrm{4cos}^{\mathrm{2}} \:\theta+\left(\mathrm{2}\:\mathrm{sin}\:\theta−\mathrm{1}\right)^{\mathrm{2}} }=\sqrt{\mathrm{5}−\mathrm{4}\:\mathrm{sin}\:\theta} \\ $$$$\mid{z}+{i}\mid=\sqrt{\mathrm{4cos}^{\mathrm{2}} \:\theta+\left(\mathrm{2}\:\mathrm{sin}\:\theta+\mathrm{1}\right)^{\mathrm{2}} }=\sqrt{\mathrm{5}+\mathrm{4}\:\mathrm{sin}\:\theta} \\ $$$${A}=\frac{\mid{z}−{i}\mid}{\mid{z}+{i}\mid}=\sqrt{\frac{\mathrm{5}−\mathrm{4}\:\mathrm{sin}\:\theta}{\mathrm{5}+\mathrm{4}\:\mathrm{sin}\:\theta}}=\sqrt{\frac{\mathrm{10}}{\mathrm{5}+\mathrm{4}\:\mathrm{sin}\:\theta}−\mathrm{1}} \\ $$$${maximum}\:{is}\:{if}\:\mathrm{sin}\:\theta=−\mathrm{1}, \\ $$$${A}_{{max}} =\sqrt{\frac{\mathrm{10}}{\mathrm{5}−\mathrm{4}}−\mathrm{1}}=\mathrm{3} \\ $$$${minimum}\:{is}\:{if}\:\mathrm{sin}\:\theta=\mathrm{1}, \\ $$$${A}_{{min}} =\sqrt{\frac{\mathrm{10}}{\mathrm{5}+\mathrm{4}}−\mathrm{1}}=\frac{\mathrm{1}}{\mathrm{3}} \\ $$

Answered by Dwaipayan Shikari last updated on 10/Jul/20

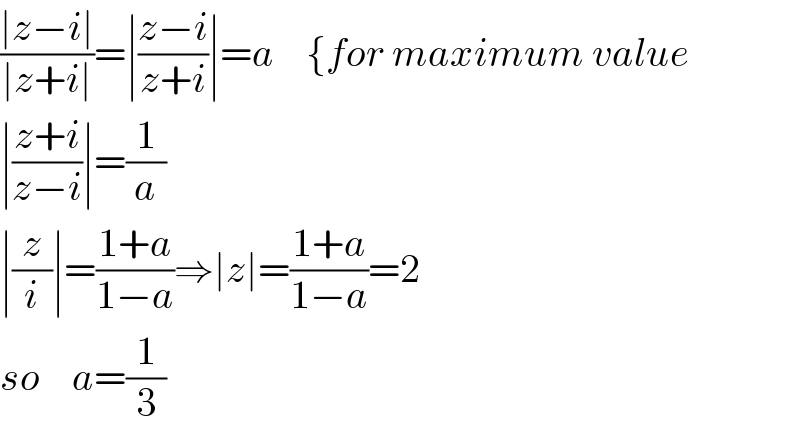
((∣z−i∣)/(∣z+i∣))=∣((z−i)/(z+i))∣=a {for maximum value ∣((z+i)/(z−i))∣=(1/a) ∣(z/i)∣=((1+a)/(1−a))⇒∣z∣=((1+a)/(1−a))=2 so a=(1/3)

$$\frac{\mid{z}−{i}\mid}{\mid{z}+{i}\mid}=\mid\frac{{z}−{i}}{{z}+{i}}\mid={a}\:\:\:\:\left\{{for}\:{maximum}\:{value}\right. \\ $$$$\mid\frac{{z}+{i}}{{z}−{i}}\mid=\frac{\mathrm{1}}{{a}} \\ $$$$\mid\frac{{z}}{{i}}\mid=\frac{\mathrm{1}+{a}}{\mathrm{1}−{a}}\Rightarrow\mid{z}\mid=\frac{\mathrm{1}+{a}}{\mathrm{1}−{a}}=\mathrm{2} \\ $$$${so}\:\:\:\:{a}=\frac{\mathrm{1}}{\mathrm{3}} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com