
Question Number 102690 by bramlex last updated on 10/Jul/20
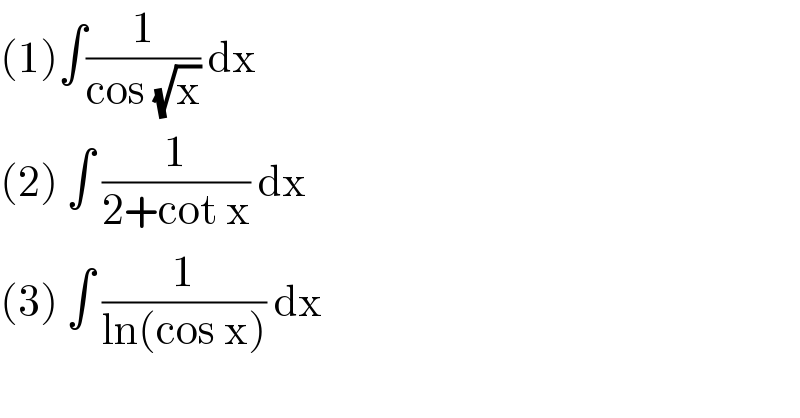
$$\left(\mathrm{1}\right)\int\frac{\mathrm{1}}{\mathrm{cos}\:\sqrt{\mathrm{x}}}\:\mathrm{dx}\: \\ $$$$\left(\mathrm{2}\right)\:\int\:\frac{\mathrm{1}}{\mathrm{2}+\mathrm{cot}\:\mathrm{x}}\:\mathrm{dx}\: \\ $$$$\left(\mathrm{3}\right)\:\int\:\frac{\mathrm{1}}{\mathrm{ln}\left(\mathrm{cos}\:\mathrm{x}\right)}\:\mathrm{dx}\: \\ $$
Answered by Dwaipayan Shikari last updated on 10/Jul/20

$$\left.\mathrm{2}\right)\int\frac{{tanx}}{\mathrm{2}{tanx}+\mathrm{1}}=\frac{\mathrm{1}}{\mathrm{2}}\int\frac{\mathrm{2}{tanx}+\mathrm{1}}{\mathrm{2}{tanx}+\mathrm{1}}−\frac{\mathrm{1}}{\mathrm{2}}\int\frac{\mathrm{1}}{\mathrm{2}{tanx}+\mathrm{1}}=\frac{{x}}{\mathrm{2}}−\frac{\mathrm{1}}{\mathrm{2}}\int\frac{\mathrm{2}}{\left(\mathrm{2}{t}+\mathrm{1}\right)\left({t}^{\mathrm{2}} +\mathrm{1}\right)}{dt} \\ $$$$ \\ $$$$=\frac{{x}}{\mathrm{2}}−\int\frac{{At}+{C}}{{t}^{\mathrm{2}} +\mathrm{1}}+\frac{{B}}{\mathrm{2}{t}+\mathrm{1}}\:\:\:\:\:\:\:\:\:\:\left\{\frac{\mathrm{1}}{\left(\mathrm{2}{t}+\mathrm{1}\right)\left({t}^{\mathrm{2}} +\mathrm{1}\right)}=\frac{{At}+{C}}{{t}^{\mathrm{2}} +\mathrm{1}}+\frac{{B}}{\mathrm{2}{t}+\mathrm{1}}\:\:{and}\:{take}\right. \\ $$$$\left({t}={tanx}\right) \\ $$$$=\frac{{x}}{\mathrm{2}}−{I}_{{a}} \:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\left\{\mathrm{2}{At}^{\mathrm{2}} +{At}+\mathrm{2}{Ct}+{C}+{Bt}^{\mathrm{2}} +{B}=\mathrm{1}\right. \\ $$$$=\frac{{x}}{\mathrm{2}}+\int\frac{\frac{\mathrm{2}}{\mathrm{5}}{t}−\frac{\mathrm{1}}{\mathrm{5}}}{{t}^{\mathrm{2}} +\mathrm{1}}−\frac{\frac{\mathrm{4}}{\mathrm{5}}}{\mathrm{2}{t}+\mathrm{1}}\:\:\:\:\:\:\:\:\:\:\:\:\:\left\{\:\:\mathrm{2}{A}+{B}=\mathrm{0}\:\:\:\:{A}+\mathrm{2}{C}=\mathrm{0}\:\:{B}+{C}=\mathrm{1}\right. \\ $$$$=\frac{{x}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{5}}\int\frac{\mathrm{2}{t}−\mathrm{1}}{{t}^{\mathrm{2}} +\mathrm{1}}−\frac{\mathrm{4}}{\mathrm{10}}\int\frac{\mathrm{1}}{{t}+\frac{\mathrm{1}}{\mathrm{2}}}{dt}\:\:\:\:\:\left\{{A}=−\frac{\mathrm{2}}{\mathrm{5}}\:\:{B}=\frac{\mathrm{4}}{\mathrm{5}}\:\:{C}=\frac{\mathrm{1}}{\mathrm{5}}\right. \\ $$$$=\frac{{x}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{5}}\int\frac{\mathrm{2}{t}}{{t}^{\mathrm{2}} +\mathrm{1}}−\frac{\mathrm{1}}{\mathrm{5}}{tan}^{−\mathrm{1}} {tanx}−\frac{\mathrm{4}}{\mathrm{10}}{log}\left({t}+\frac{\mathrm{1}}{\mathrm{2}}\right) \\ $$$$=\frac{{x}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{5}}{log}\left({t}^{\mathrm{2}} +\mathrm{1}\right)−\frac{\mathrm{1}}{\mathrm{5}}{x}−\frac{\mathrm{4}}{\mathrm{10}}{log}\left({tanx}+\frac{\mathrm{1}}{\mathrm{2}}\right) \\ $$$$=\frac{{x}}{\mathrm{2}}+\frac{\mathrm{2}}{\mathrm{5}}{log}\left({secx}\right)−\frac{\mathrm{1}}{\mathrm{5}}{x}−\frac{\mathrm{4}}{\mathrm{10}}{log}\left({tanx}+\frac{\mathrm{1}}{\mathrm{2}}\right)+{Constant} \\ $$$$=\frac{\mathrm{1}}{\mathrm{5}}\left(\mathrm{2}{x}−{log}\left({cosx}\right)−\mathrm{2}{log}\left({tanx}+\frac{\mathrm{1}}{\mathrm{2}}\right)\right)+{Constant} \\ $$
Answered by mathmax by abdo last updated on 10/Jul/20

$$\left.\mathrm{2}\right)\:\mathrm{I}\:=\int\:\:\frac{\mathrm{dx}}{\mathrm{2}+\frac{\mathrm{cosx}}{\mathrm{sinx}}}\:\Rightarrow\:\mathrm{I}\:=\int\:\:\frac{\mathrm{sinx}}{\mathrm{2sinx}\:+\mathrm{cosx}}\mathrm{dx}\:\mathrm{changement}\:\mathrm{tan}\left(\frac{\mathrm{x}}{\mathrm{2}}\right)=\mathrm{t}\:\mathrm{give} \\ $$$$\mathrm{I}\:=\int\:\:\frac{\frac{\mathrm{2t}}{\mathrm{1}+\mathrm{t}^{\mathrm{2}} }}{\mathrm{2}×\frac{\mathrm{2t}}{\mathrm{1}+\mathrm{t}^{\mathrm{2}} }\:+\frac{\mathrm{1}−\mathrm{t}^{\mathrm{2}} }{\mathrm{1}+\mathrm{t}^{\mathrm{2}} }}\:\mathrm{dt}\:=\int\:\:\frac{\mathrm{2t}}{\mathrm{4t}+\mathrm{1}−\mathrm{t}^{\mathrm{2}} }\:\mathrm{dt}\:=−\mathrm{2}\:\int\:\:\frac{\mathrm{tdt}}{\mathrm{t}^{\mathrm{2}} −\mathrm{4t}−\mathrm{1}} \\ $$$$\mathrm{t}^{\mathrm{2}} −\mathrm{4t}−\mathrm{1}\:=\mathrm{0}\:\rightarrow\Delta^{'} \:=\mathrm{4}+\mathrm{1}\:=\mathrm{5}\:\Rightarrow\mathrm{t}_{\mathrm{1}} =\mathrm{2}+\sqrt{\mathrm{5}}\:\mathrm{and}\:\mathrm{t}_{\mathrm{2}} =\mathrm{2}−\sqrt{\mathrm{5}} \\ $$$$\Rightarrow\:\mathrm{F}\left(\mathrm{t}\right)\:=\frac{\mathrm{t}}{\mathrm{t}^{\mathrm{2}} −\mathrm{4t}−\mathrm{1}}\:=\frac{\mathrm{t}}{\left(\mathrm{t}−\mathrm{t}_{\mathrm{1}} \right)\left(\mathrm{t}−\mathrm{t}_{\mathrm{2}} \right)}\:=\frac{\mathrm{a}}{\mathrm{t}−\mathrm{t}_{\mathrm{1}} }\:+\frac{\mathrm{b}}{\mathrm{t}−\mathrm{t}_{\mathrm{2}} } \\ $$$$\mathrm{a}\:=\frac{\mathrm{t}_{\mathrm{1}} }{\mathrm{t}_{\mathrm{1}} −\mathrm{t}_{\mathrm{2}} }\:=\frac{\mathrm{2}+\sqrt{\mathrm{5}}}{\mathrm{2}\sqrt{\mathrm{5}}}\:,\:\mathrm{b}\:=\frac{\mathrm{t}_{\mathrm{2}} }{\mathrm{t}_{\mathrm{2}} −\mathrm{t}_{\mathrm{1}} }\:=\frac{\mathrm{2}−\sqrt{\mathrm{5}}}{−\mathrm{2}\sqrt{\mathrm{5}}}\:=\frac{−\mathrm{2}+\sqrt{\mathrm{5}}}{\mathrm{2}\sqrt{\mathrm{5}}}\:\Rightarrow \\ $$$$\mathrm{I}\:=−\mathrm{2}\:\int\:\:\:\frac{\mathrm{adt}}{\mathrm{t}−\mathrm{t}_{\mathrm{1}} }\:−\mathrm{2}\:\int\:\frac{\mathrm{bdt}}{\mathrm{t}−\mathrm{t}_{\mathrm{2}} } \\ $$$$=−\mathrm{2aln}\mid\mathrm{t}−\mathrm{t}_{\mathrm{1}} \mid\:−\mathrm{2}\:\mathrm{b}\:\mathrm{ln}\mid\mathrm{t}−\mathrm{t}_{\mathrm{2}} \mid\:+\mathrm{c} \\ $$$$=−\mathrm{2}×\frac{\mathrm{2}+\sqrt{\mathrm{5}}}{\mathrm{2\%5}}\mathrm{ln}\mid\mathrm{tan}\left(\frac{\mathrm{x}}{\mathrm{2}}\right)−\mathrm{2}−\sqrt{\mathrm{5}}\mid−\mathrm{2}×\frac{−\mathrm{2}+\sqrt{\mathrm{5}}}{\mathrm{2}\sqrt{\mathrm{5}}}\mathrm{ln}\mid\mathrm{tan}\left(\frac{\mathrm{x}}{\mathrm{2}}\right)−\mathrm{2}+\sqrt{\mathrm{5}}\mid\:+\mathrm{C} \\ $$$$=\left(\frac{−\mathrm{2}−\sqrt{\mathrm{5}}}{\sqrt{\mathrm{5}}}\right)\mathrm{ln}\mid\mathrm{tan}\left(\frac{\mathrm{x}}{\mathrm{2}}\right)−\mathrm{2}−\sqrt{\mathrm{5}}\mid\:+\frac{\mathrm{2}−\sqrt{\mathrm{5}}}{\sqrt{\mathrm{5}}}\mathrm{ln}\mid\mathrm{tan}\left(\frac{\mathrm{x}}{\mathrm{2}}\right)−\mathrm{2}+\sqrt{\mathrm{5}}\mid\:+\mathrm{C} \\ $$
Answered by bemath last updated on 11/Jul/20

