Question Number 102698 by bramlex last updated on 10/Jul/20

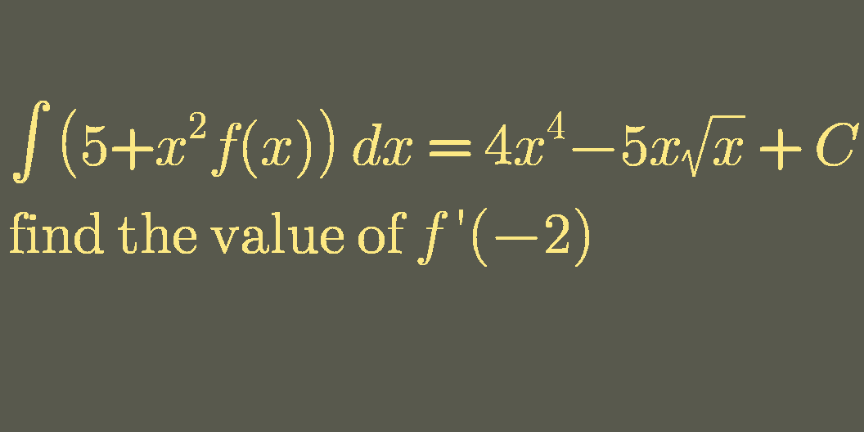
Answered by bramlex last updated on 10/Jul/20

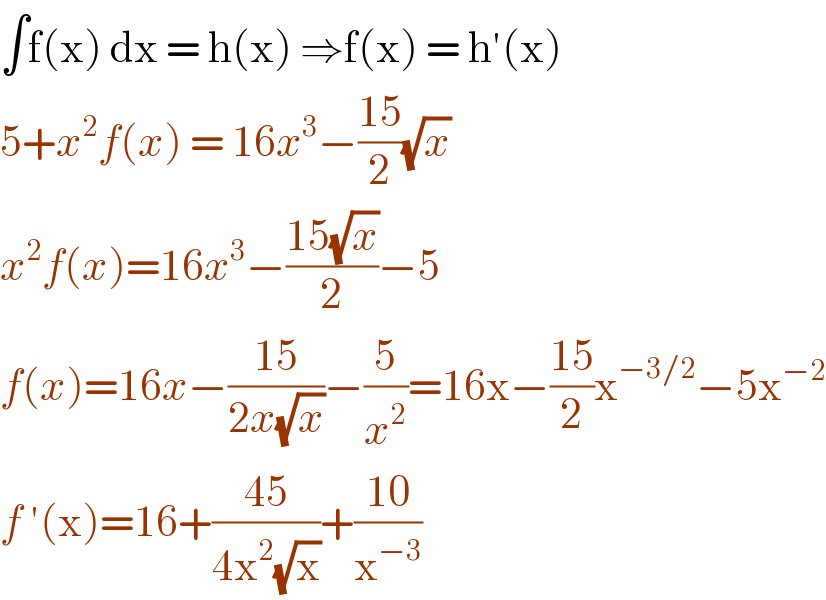
∫f(x) dx = h(x) ⇒f(x) = h′(x) 5+x^2 f(x) = 16x^3 −((15)/2)(√x) x^2 f(x)=16x^3 −((15(√x))/2)−5 f(x)=16x−((15)/(2x(√x)))−(5/x^2 )=16x−((15)/2)x^(−3/2) −5x^(−2) f ′(x)=16+((45)/(4x^2 (√x)))+((10)/x^(−3) )

Answered by floor(10²Eta[1]) last updated on 10/Jul/20

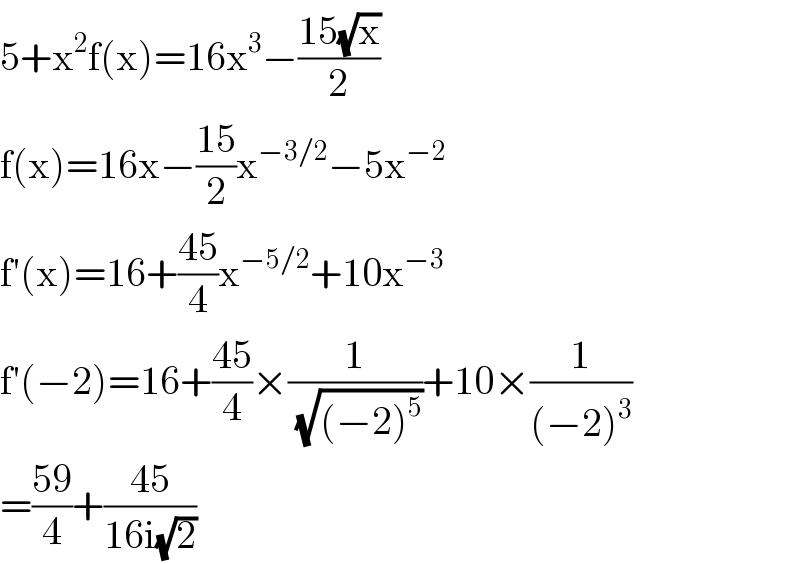
5+x^2 f(x)=16x^3 −((15(√x))/2) f(x)=16x−((15)/2)x^(−3/2) −5x^(−2) f′(x)=16+((45)/4)x^(−5/2) +10x^(−3) f′(−2)=16+((45)/4)×(1/(√((−2)^5 )))+10×(1/((−2)^3 )) =((59)/4)+((45)/(16i(√2)))

Commented bybramlex last updated on 10/Jul/20

⌣•⌣•⌣